“复杂系统 Complex Systems”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
第8行： 第8行：
  
  
−
复杂系统是指那些本身难以直接建模的系统，因为系统组成元素之间以及系统和环境之间存在依赖、竞争、关联等复杂的相互作用。系统之所以“复杂”，是因为在这些相互作用中会产生如[[非线性 nonlinearity]]、[[涌现 emergence]]、[[自发秩序 spontaneous order]] 、[[适应性 adaptation]]以及反馈回路 feedback loops等特殊性质。因为这些系统出现在不同领域，所以对不同领域系统的共性研究慢慢发展成为一个独立的研究领域。大部分情况下，复杂系统都可以表示成一个网络，网络中的节点表示元素，连边表示相互作用。
+
复杂系统是指那些本身难以直接建模的系统，因为系统组成元素之间以及系统和环境之间存在依赖、竞争、关联等复杂的相互作用。系统之所以“复杂”，是因为在这些相互作用中会产生如'''非线性 nonlinearity'''、'''涌现 emergence'''、'''自发秩序 spontaneous order''' 、'''适应性 adaptation'''以及'''反馈回路 feedback loops'''等特殊性质。因为这些系统出现在不同领域，所以对不同领域系统的共性研究慢慢发展成为一个独立的研究领域。大部分情况下，复杂系统都可以表示成一个网络，网络中的节点表示元素，连边表示相互作用。
  
 
复杂系统理论是系统科学中的一个前沿方向，它是复杂性科学的主要研究任务。复杂性科学被称为21 世纪的科学，它的主要目的就是要揭示复杂系统的一些难以用现有科学方法解释的动力学行为。与传统的还原论方法不同，复杂系统理论强调用整体论和还原论相结合的方法去分析系统。目前，复杂系统理论还处于萌芽阶段，它可能蕴育着一场新的系统学乃至整个传统科学方法的革命。生命系统、社会系统都是复杂系统，复杂系统理论的应用在系统生物学的研究与生物系统计算机数学建模中具有重要的意义。
 
复杂系统理论是系统科学中的一个前沿方向，它是复杂性科学的主要研究任务。复杂性科学被称为21 世纪的科学，它的主要目的就是要揭示复杂系统的一些难以用现有科学方法解释的动力学行为。与传统的还原论方法不同，复杂系统理论强调用整体论和还原论相结合的方法去分析系统。目前，复杂系统理论还处于萌芽阶段，它可能蕴育着一场新的系统学乃至整个传统科学方法的革命。生命系统、社会系统都是复杂系统，复杂系统理论的应用在系统生物学的研究与生物系统计算机数学建模中具有重要的意义。
第16行： 第16行：
 
== 概览 ==
 
== 概览 ==
  
−
''复杂系统''这一术语，通常是指对复杂系统的研究，表示一种新的科学研究方法。主要研究系统元素之间的关系如何产生集体行为，系统和环境之间如何进行相互作用，将集体、系统层面的行为作为研究的基本对象<ref>Bar-Yam (2014) [https://pattern.swarma.org/paper?id=bf882316-6e74-11ea-befb-0242ac1a0005 "General Features of Complex Systems"].Yaneer, Encyclopedia of Life Support Systems. Retrieved 16 September.</ref>。因此，复杂系统可以看作是[[还原论 reductionism]]的替代范式，主要解释系统的组成部分和相互关系。
+
''复杂系统''这一术语，通常是指对复杂系统的研究，表示一种新的科学研究方法。主要研究系统元素之间的关系如何产生集体行为，系统和环境之间如何进行相互作用，将集体、系统层面的行为作为研究的基本对象<ref>Bar-Yam (2014) [https://pattern.swarma.org/paper?id=bf882316-6e74-11ea-befb-0242ac1a0005 "General Features of Complex Systems"].Yaneer, Encyclopedia of Life Support Systems. Retrieved 16 September.</ref>。因此，复杂系统可以看作是'''还原论 reductionism'''的替代范式，主要解释系统的组成部分和相互关系。
  
 
作为一个跨学科的研究领域，复杂系统吸收了许多其他领域的研究理论，如借鉴物理学对[[自组织 self-organization]]的研究，社会科学对[[自发秩序 spontaneous order]]的研究，数学对[[混沌 chaos]]的研究，生物学对[[适应性 adaptation]]的研究。因此“复杂系统”是一个宽泛的术语，涵盖了不同领域的研究方法，包括统计物理学、信息论、非线性动力学、人类学、计算机科学、气象学、社会学、经济学、心理学和生物学等。
 
作为一个跨学科的研究领域，复杂系统吸收了许多其他领域的研究理论，如借鉴物理学对[[自组织 self-organization]]的研究，社会科学对[[自发秩序 spontaneous order]]的研究，数学对[[混沌 chaos]]的研究，生物学对[[适应性 adaptation]]的研究。因此“复杂系统”是一个宽泛的术语，涵盖了不同领域的研究方法，包括统计物理学、信息论、非线性动力学、人类学、计算机科学、气象学、社会学、经济学、心理学和生物学等。
 +
 +
===复杂系统的共性===
 +
 +
* 个人一般都遵循相对简单的规则，不存在中央控制或者领导者。
 +
* 大量个体的集体行为产生出了复杂、不断变化而且难以预测的行为模式。
 +
* 利用来自内部和外部环境中的信息和信号，同时也产生信息和信号。
 +
* 可以通过学习和进化过程进行适应，即改变自身的行为以增加生存或成功的机会。
 +
'''总结'''：复杂系统由大量组分组成的网络，不存在中央控制，通过简单运作规则产生出复杂的集体行为和复杂的信息处理，并通过学习和进化产生适应性。
 +
  
 
== 重要概念 ==
 
== 重要概念 ==

2020年4月11日 (六) 10:50的版本


复杂系统 complex system由许多相互作用的元素组成。复杂系统的例子无处不在：全球气候、有机体、人脑、电网、交通、通讯系统等基础设施网络、城市社会和经济组织网络、生态系统、活细胞、甚至整个宇宙，这些都可以看作是复杂系统。


复杂系统是指那些本身难以直接建模的系统，因为系统组成元素之间以及系统和环境之间存在依赖、竞争、关联等复杂的相互作用。系统之所以“复杂”，是因为在这些相互作用中会产生如非线性 nonlinearity、涌现 emergence、自发秩序 spontaneous order 、适应性 adaptation以及反馈回路 feedback loops等特殊性质。因为这些系统出现在不同领域，所以对不同领域系统的共性研究慢慢发展成为一个独立的研究领域。大部分情况下，复杂系统都可以表示成一个网络，网络中的节点表示元素，连边表示相互作用。

复杂系统理论是系统科学中的一个前沿方向，它是复杂性科学的主要研究任务。复杂性科学被称为21 世纪的科学，它的主要目的就是要揭示复杂系统的一些难以用现有科学方法解释的动力学行为。与传统的还原论方法不同，复杂系统理论强调用整体论和还原论相结合的方法去分析系统。目前，复杂系统理论还处于萌芽阶段，它可能蕴育着一场新的系统学乃至整个传统科学方法的革命。生命系统、社会系统都是复杂系统，复杂系统理论的应用在系统生物学的研究与生物系统计算机数学建模中具有重要的意义。

复杂系统涵盖的主题

概览

复杂系统这一术语，通常是指对复杂系统的研究，表示一种新的科学研究方法。主要研究系统元素之间的关系如何产生集体行为，系统和环境之间如何进行相互作用，将集体、系统层面的行为作为研究的基本对象[1]。因此，复杂系统可以看作是还原论 reductionism的替代范式，主要解释系统的组成部分和相互关系。

作为一个跨学科的研究领域，复杂系统吸收了许多其他领域的研究理论，如借鉴物理学对自组织 self-organization的研究，社会科学对自发秩序 spontaneous order的研究，数学对混沌 chaos的研究，生物学对适应性 adaptation的研究。因此“复杂系统”是一个宽泛的术语，涵盖了不同领域的研究方法，包括统计物理学、信息论、非线性动力学、人类学、计算机科学、气象学、社会学、经济学、心理学和生物学等。

复杂系统的共性

  • 个人一般都遵循相对简单的规则，不存在中央控制或者领导者。
  • 大量个体的集体行为产生出了复杂、不断变化而且难以预测的行为模式。
  • 利用来自内部和外部环境中的信息和信号，同时也产生信息和信号。
  • 可以通过学习和进化过程进行适应，即改变自身的行为以增加生存或成功的机会。

总结：复杂系统由大量组分组成的网络，不存在中央控制，通过简单运作规则产生出复杂的集体行为和复杂的信息处理，并通过学习和进化产生适应性。


重要概念

系统

复杂系统主要关注的是系统的行为和性质。一个系统 system，广义地讲，是由一组实体，通过实体之间的交互、关联、或者依赖，形成一个统一的整体。系统一般由边界来定义，边界决定了哪些属于系统内的一部分，而位于系统边界之外的部分则构成了该系统的环境。一个系统可以表现出与系统个体行为和性质不一样的特性。这些系统层面（整体）的性质和特征通过系统与环境相互作用，或者由系统的部分行为体现出来（例如，对外部刺激作出反应）。“行为”的概念意味着，研究系统也涉及到对随时间演化的过程研究（或者，在数学中，叫做相空间参数化）。 由于其广泛的、跨学科的适用性，系统是复杂系统中极其重要的概念。

开放系统的输入和输出流，代表系统和周围环境之间的问题、能量和信息之间的交换

作为一个研究领域，复杂系统是系统论的一个子领域。 尽管广义的系统理论也侧重于研究相互作用实体的集体行为，但复杂系统研究的是更广泛的一类系统，包括传统还原论方法也能适用的非复杂系统。事实上，系统理论试图探索和描述所有类型的系统，主要目标就是发明对各研究领域都有用的理论。

至于系统理论和复杂系统的关系，系统理论强调系统各部分之间的关系和依赖在一定程度上决定了整个系统的性质，有助于说明复杂系统的跨学科研究视角：共享属性的概念连接了不同领域的系统，证明无论是什么样的复杂系统，都可以通过建模方法对系统进行科学研究。同时复杂系统重要的特定概念，如涌现 emergence、反馈回路 feedback loops和适应性 adaptation，也起源于系统理论。

复杂性

“系统表现出复杂性”意味着很难从其行为中推断出系统的性质。任何忽略这些差异和特性，或者将差异和特性视为噪声的建模方法都是不准确也没有效果的。到目前为止，还没有完全通用的复杂系统理论来解决这些问题，因此研究人员必须结合特定的领域解决问题。研究人员解决这些问题的方法是将建模的主要任务看做是刻画复杂性，而不简化系统的复杂性。

虽然目前还没有被广泛认可的复杂性的精确定义，但是有很多关于复杂性的典型例子。例如，如果系统具有混沌行为(对初始条件表现出极度敏感的行为) ，或者如果它们具有涌现特性(这些特性从它们的组成元素中看不出来，但来源于在一个系统中产生的关系和依赖) ，或者如果它们难以计算建模(如果它们的参数数量的增加快于系统大小的增加) ，那么系统就可能是复杂的。

网络

复杂系统中相互作用的部分组成一个网络，网络是离散对象及其相互关系的集合，通常描述为由边连接的顶点图。 网络可以描述系统中个体之间的关系，电路中逻辑门之间的关系，基因调控网络中的基因之间的关系，或者任何其他相关实体之间的关系。

网络经常用来刻画复杂系统中的复杂性。因此，把复杂系统当作网络来研究，可以使图论和网络科学 network science得到广泛应用。例如，一些复杂系统也是复杂网络，它们具有相变和幂律度分布等特性，这些特性容易导致涌现或混沌行为。一个完全图中，边的数量随着顶点数量的增加而幂次增长，这一特性进一步揭示了大型网络中复杂性的来源: 随着网络的增长，实体之间的关系增加要远快于实体数量的增加。

非线性

复杂系统通常具有非线性行为，意味着输入相同的状态和内容，系统可能会作出不同的回应。在数学和物理学中，非线性描述的是输入和输出不成比例的系统。当给定输入变化时，系统产生的结果可能远大于或远小于输入的变化，甚至根本没有输出（这取决于系统当前的状态或参数值的取值）。

洛伦兹吸引子当 ρ = 28, σ = 10, and β = 8/3 [2]

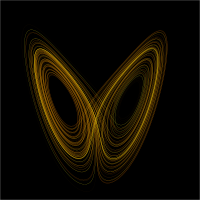
复杂系统中一个有意思的研究就是非线性动力系统，它是由一个或多个非线性项组成的微分方程组。一些非线性动力系统，如洛伦兹系统，可以产生一种称为混沌的数学现象。 混沌，适用于复杂系统，通常是指是指对初始条件的敏感依赖，如“蝴蝶效应” 。在这样一个系统中，小的初始改变状态可能会导致截然不同的结果。因此，混沌行为的数值模拟非常困难，因为在计算的中间阶段，很小的扰动误差会导致模型产生极为不准确的结果。此外，如果一个复杂的系统回到一个之前的初始状态，它可能会表现出和之前状态完全不一样的行为，完全不同的行为反应相同的刺激，所以混沌也对经验推断的方式提出了挑战。

涌现

复杂系统的另一个共同特征是涌现行为和特性的存在：这些是系统层面的特征，无法从其组成部分中孤立地表现出来，而是由它们在系统中一起形成的相互作用、依赖或关系所形成。涌现广泛地描述了这类行为的出现，并且在社会科学和物理科学研究的系统中都有广泛应用。涌现通常是指复杂系统中出现的无计划却有组织的行为，也可以指系统的崩溃，可用于描述从组成系统的较小实体层面难以预测或无法预测的现象。

康威生命游戏中出现的枪型的元胞自动机

在复杂系统中，涌现特性被广泛研究的其中一个例子就是元胞自动机 Cellular Automata。在元胞自动机中，一个由细胞组成的网格，每个细胞都是处于某种状态，且这些状态是有限的，然后根据一组简单的规则进行演化。这些规则指导每个细胞与其邻近细胞进行“相互作用”。 尽管这些规则只是局部定义的，但是它们已经被证明能够产生全局性的有趣行为，例如康威的生命游戏 Conway's Game of Life。

自发秩序与自组织

当涌现用于描述无计划的秩序出现时，是指自发秩序(在社会科学中)或自组织(在物理科学中)。自发秩序可以在羊群行为中看到，即一群个体在没有集中计划安排的情况下协调他们的行动；在某些晶体的整体对称性中可以看到自组织，例如雪花的径向对称性，这种对称性来自于水分子与其周围环境之间的局部吸引力和排斥力。

适应

复杂适应系统 Complex Adaptive Systems，简称CAS，是复杂系统的特例，这类系统具有改变和从经验中学习的能力，因此具有适应性。复杂适应系统的例子包括股票市场，社会昆虫，蚁群、生物圈和生态系统，大脑和免疫系统、细胞和发育中的胚胎，城市、制造业和在文化和社会系统中比如政党或者社区等人类社会群体活动。 [3]

功能

复杂系统可能具有以下特征[4]：

级联失效

由于复杂系统中组成部分之间的强耦合性，一个或多个组成部分的失效可能导致级联失效，这可能对系统的运行造成灾难性的后果[5]。局部攻击可能导致空间网络的级联失效或突然崩溃。[6]

开放系统

复杂系统通常是开放系统，即存在热力学梯度和耗散能量。换句话说，复杂系统经常远离能量平衡态: 但是尽管存在这种变动，仍然可能存在稳定的模式，参见协同作用 synergetics。

系统演化

一个系统的演化过程可能是非常重要的，因为复杂系统是随着时间演化的动力系统，历史状态可能对当前状态有影响。 更正式地说，复杂系统往往表现出自发故障 spontaneous failures、恢复 recovery 以及磁滞 hysteresis。[7]。 当延迟的负反馈导致振荡或其他复杂动力学变弱时[8]，系统状态空间中的“临界减速方向”可能预示着系统在这种“临界转换”之后的未来状态。相互作用系统可能具有许多相变的复杂滞后现象。[9]

系统嵌套

复杂系统的组成部分也可能是一个复杂系统。 例如，一个经济体是由组织构成的，这些组织是由人构成的，这些人是由细胞构成的——而所有这些（经济体、组织、人、细胞）都可以看作是复杂系统。 在复杂的二分网络中，相互作用的排列也可以是嵌套的。 更具体地说，互相进行有益交互的二分生态和组织网络被发现具有嵌套结构。[10] [11] 这种结构提高了间接促进作用和系统在日益严峻的环境下持续存在的能力，以及大规模系统性政权转移的可能性。[12] [13]

网络动力学多样性

除了有耦合规则，复杂系统的网络动力学也是非常重要的。局部相互作用以及少数优先连接在小世界网络或无标度网络[14][15][16]经常被应用，特别是自然复杂系统经常表现出这样的拓扑结构。 例如，在人类的大脑皮层，我们可以看到密集的局部连接，以及一些非常长的轴突在大脑皮层内部和其他大脑区域之间的投射。

涌现现象的产生

复杂系统很多行为都是涌现的。也就是说，虽然结果可能由系统的基本组成部分的活动决定的，但它们需要从更高的层次进行研究分析。 例如，在蚁丘中的白蚁具有生理学特征、生物化学特征和生物学的发育特征，这些都处于一个分析层面的，但是它们的社会行为和蚁丘的建造是白蚁集体层面涌现出来的属性，需要在不同的层面上进行分析。

非线性关系

实际上，这意味着一个小的扰动可能会引发大的效应(见蝴蝶效应 butterfly effect) 或者一个成比例的效应或者甚至根本没有效应。 在线性系统中，效应总是与输入成比例。 而非线性 nonlinearity则相反。

反馈循环

在复杂系统中，经常会存在负反馈和正反馈。 元素行为的影响以元素本身被改变的方式反馈到系统中。

历史

复杂性科学发展地图[17]

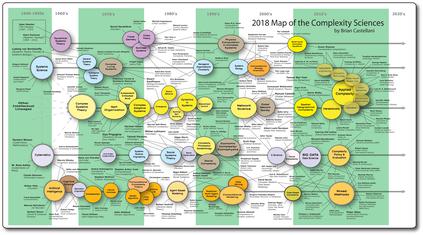
可以说，人类研究复杂系统已有数千年的历史，但与物理和化学等已确立的科学领域相比，复杂系统的现代科学研究还相对年轻。 系统科学的研究历史和几种不同的研究趋势有关。

在数学领域，可以说对复杂系统研究的最大贡献是发现了确定性系统中混沌 chaos现象，在某些特定的动力系统有一个重要的特征也与数学有关，即非线性 nonlinearity。[18]神经网络研究的数学部分在推进复杂系统的研究中也是不可或缺的。

自组织系统的概念与非平衡热力学中的研究有关，化学先驱和诺贝尔奖获得者伊利亚 · 普里高金 Ilya Prigogine在他的耗散结构 dissipative structures研究中首次提到这个概念。 更久远的可以追溯到 Hartree-Fock关于量子化学方程的工作，以及后来对分子结构的计算，这些可以被看作是科学上涌现和整体涌现最早的例子之一。

一个包含人类的复杂系统是苏格兰启蒙运动的古典政治经济学，后来由奥地利经济学派发展，认为市场系统的秩序是自发的(或涌现的) ，因为它是人类行为的结果，而不是任何人类设计的执行。[19][20]

在此基础上，奥地利学派从19世纪到20世纪发展了早期的经济计算 economic calculation problem问题，随后提出了分散知识 dispersed knowledge的概念（即没有一个单一的行为主体拥有影响整个系统的价格和生产的所有因素的信息），这一概念引发了对当时占主导地位的凯恩斯主义的争论。 这场争论引起了经济学家、政治家和其他政党对计算复杂性问题的关注。

诺贝尔经济学奖得主、哲学家弗里德里希·哈耶克 F. A. Hayek是这一领域的先驱，受到卡尔•波普尔 Karl Popper和沃伦•韦弗 Warren Weaver 著作的启发，从20世纪早期到晚期，他的大部分工作致力于研究复杂现象[21]，，不是将他的工作局限于人类经济，而是涉足心理学[22]、生物学和控制论等其他领域。格雷戈里 · 贝特森 Gregory Bateson在建立人类学和系统论之间的联系方面发挥了关键作用：他指出文化的互动部分很像生态系统。

虽然对复杂系统的明确研究至少可以追溯到20世纪70年代[23]，但第一个专注于复杂系统的研究机构是圣塔菲研究所 Santa Fe Institute，成立于1984年[24][25]。 圣菲研究所的早期参与者包括诺贝尔物理学奖得主默里·盖尔曼 Murray Gell-Mann和 菲利普·安德森 Philip Anderson，诺贝尔经济学奖得主 肯尼思·阿诺 Kenneth Arrow，以及曼哈顿计划的科学家乔治·考温 George Cowan 和 赫伯·安德森 Herb Anderson[26]。到现在已经有50多个专注于复杂系统研究所和研究中心。

应用

实践中的复杂性

传统的处理复杂性的方法是减少或限制的方式。通常情况下，这涉及到部门化 compartmentalization: 将一个大的系统划分成独立的部分。 例如，组织将他们的工作分成不同的部门，每个部门处理不同的问题。 工程系统设计通常采用模块化组件。 然而，当部门之间的连接出现问题时，模块化设计很容易失败。

复杂性管理

随着项目和收购变得越来越复杂，公司和政府面临着挑战去找到有效方法来管理大型收购，例如：陆军未来战斗系统（FCS）。FCS收购依赖于相互关联的部分，而它们之间的相互作用是无法预测的，随着收购变得越来越以网络为中心和复杂化，企业将被迫设法管理复杂性，而政府将面临挑战去提供有效治理，以确保灵活性和韧性 resiliency。[27]

复杂经济学

在过去的几十年里，在复杂经济学 complexity ecomomics的新兴领域中，新的预测模型已经被开发出来,用于解释经济增长。比如1989年由圣菲研究所建立的模型（人工股票市场模型），以及最近由麻省理工学院物理学家塞萨尔·伊达尔戈 César A. Hidalgo和哈佛大学经济学家 里卡多 · 豪斯曼 Ricardo Hausmann 提出的经济复杂性指数 economic complexity index 。基于ECI指数，Hausmann、Hidalgo 和他们的经济复杂性观测站团队已经做出了2020年的 GDP 预测。

复杂性与教育

福斯曼 Forsman、莫尔 Moll 和林德 Linder关注学生持续学习的问题，探讨了“将复杂性科学作为一个框架来扩展物理教育研究 physics education research法应用的可行性” ，发现“在复杂性科学的视角内构建社会网络分析，为广泛的物理教育研究PER主题提供了新的强大的适用性”。 [28]

复杂性与建模

弗里德里希·哈耶克 F. A. Hayek对早期复杂性理论的主要贡献之一，是他对“人类预测简单系统行为的能力”与“透过建模预测复杂系统行为的能力”二者之间的区别。 他认为，经济学和一般复杂现象的科学一样，都包括生物学、心理学等等，不能像物理处理本质上简单现象一样去建模[29]。哈耶克明确地解释了通过建模的复杂现象，只能对模式进行预测，而不能对非复杂现象进行精确的预测。[30]

复杂性与混沌理论

复杂性理论起源于混沌理论，而混沌理论又起源于一个多世纪前法国数学家朱尔斯·亨利·庞加莱 Jules HenriPoincaré的著作。混沌有时被视为极其复杂的信息，而不是无序信息。[31]混沌系统扔保持确定性，尽管它们的长期行为很难精确预测。 通过对初始条件和描述混沌系统行为的相关方程等完整的信息，人们可以在理论上对系统做出完美的精确预测，尽管在实践中这是不可能做到任意精确。 伊利亚 · 普里高金 Ilya Prigogine认为[32] 复杂性是不确定的，无论如何都无法精确地预测未来。[33]

复杂性理论中的涌现展示了一个介于确定性秩序和随机性之间复杂的领域[34]。 这被称为“混乱的边缘” edge of chaos。[35]

洛伦兹的蝴蝶.

在分析复杂系统时，对初始条件的敏感性不如在混沌理论中那样重要。正如科兰德 Colander 所说[36]，复杂性研究是混沌研究的对立面。 复杂性是指大量极其复杂和动态变化的关系集合如何产生一些简单的行为模式，而确定性混沌意义上的混沌行为，则是一些相对少量非线性相互作用的结果。[34]

因此，混沌系统与复杂系统的主要区别在于二者对历史演化的依赖性。 混乱的系统不像复杂的系统那样依赖于历史数据[37]。 混沌行为将一个处于平衡状态的系统推向混沌状态，换句话说，系统超出了我们传统定义的“有序”。另一方面，复杂系统是指系统从混沌的边缘，即远离平衡状态演化。 它们演变到一个临界状态，这个临界状态是由不可逆和意料之外的事件累积而成的，物理学家默里·盖尔曼称之为“冻结事故的积累”an accumulation of frozen accidents[38]。在某种意义上，混沌系统可以被看作是复杂系统的一个子集。 它对历史数据没有依赖性。许多真正的复杂系统，在有限周期内具备鲁棒性。 然而，它们确实具有在保持系统完整性的同时发生根本性质变化的潜力。 质变可能不仅仅是这种转变的隐喻。

复杂性与网络科学

一个复杂的系统通常由许多组成部分及其相互作用组成。 这样一个系统可以用一个网络来表示，其中节点代表组成部分，连边代表它们之间的相互作用。[16] [39][40][41]例如，因特网可以表示为一个由节点(计算机)和连边(计算机之间的直接连接)组成的网络。 利用渗流理论 percolation theory [42]研究了其对故障的恢复能力。 其他的例子还有社交网络、航空公司网络[43]、生物网络和气候网络[44]，网络也可能失效也会自动恢复。 为了建立这种现象的模型，可以查看 Majdandzic 等人的研究[7]。复杂系统之间的相互作用也可以被建模为网络的网络。 关于它们的故障和恢复特性，见 Gao 等人的研究[45] [9]。城市交通可以表示为一个网络，加权链路表示两个节点(节点)之间的速度。 这种方法在衡量一个城市的整体交通效率时是很有用的[46]。 有关交通及其他基础设施[47]系统韧性 resilience的定义，可以参考这个[48]。

复杂性的一般计算形式

建立了有序系统的可达最优性计算形式[49]，揭示了在系统完整性的一般限制内，复杂性计算是有序系统的特定和任何经验路径下的“最优选择”和“最优驱动达成模式超时”的复合计算。

可达成优选的计算定律有四个关键组成成分，如下所述：

1. 最优可达性 Reachability of Optimality：任何预期的最优应该是可达的。对于有序系统的成员，甚至是有序系统本身，不可达的最优性都是没有意义的。

2. 主导性和一致性 Prevailing and Consistency：极大化可达性以探索最佳可利用的最优，是有序系统中所有成员的普遍性计算逻辑，并且适应于有序系统。

3. 条件性 Conditionality ：可达成性和最优之间可以实现的取舍，主要取决于初始投注能力以及投注能力如何随投注行为触发的收益表更新路径而演变、如何由基本的奖惩规则赋值。准确地说，这是一系列有条件的事件，下一个事件将发生于从经验路径到达现状之时。

4. 稳健性 Robustness：可达成最优所能承受的挑战越多，就路径完整性而言就越稳健。

可达成优选定律中也有四个计算特征。

1. 最佳选择 Optimal Choice：实现最佳选择的计算可以是非常简单、也可以非常复杂。在最佳选择中的一个简单规则，就是接受所达成的任何事情。“按件奖励”RAYG，当 RAYG 被采用时，可达最优计算将减少到最优化的可达性。当达成的游戏中存在多个 NE 策略时，最优选择计算可能更为复杂。

2. 初始状态 Initial Status：计算被假设从一个有兴趣的起点开始，甚至一个有序系统的绝对起点本质上可能不存在，也不需要存在。假设的中性初始状态有利于人工或模拟计算，预计不会改变任何发现的普遍性。

3. 领域 Territory：一个有序系统应该有一个域，由系统发起的通用计算，将产生一个仍然在域内的最优解。

4. 达成模式 Reaching Pattern：在计算空间中的达成模式、或者在计算空间中的最优驱动达成模式的形式，主要依赖于计算空间下度量空间的性质和维度、以及实现可达的经验路径的惩罚和奖励规则。我们感兴趣的经验路径有五种基本形式：持续正向增强经验路径、持续负向增强经验路径、混合持续型经验路径、衰减规模经验路径、和选择经验路径。

在选择经验路径中的复合计算，包括当前和滞后交互作用、动态拓扑变换，并且暗示有序系统的经验路径具有不变性和变异的特征。

在选择经验路径中的复合计算，包括当前和滞后交互作用、动态拓扑变换，并且在有序系统的经验路径表现出不变性和变异的特征。

同时，可达成最优的计算形式给出了复杂性模型、混沌性模型、和确定性模型之间的界限。当 “按件奖励”RAYG是最优选择计算，并且可达模式是持续正向经验路径、持续负向经验路径、或混合持久模式经验路径时，其底层计算应该是采用确定规则的简单系统计算。如果可达模式没有在 RAYG 体制中经历的持续模式，基础计算则提示有混沌系统。当最佳选择计算涉及非 RAYG 计算时，此为复杂性计算所驱动的复合效应。

著名学者

相关概念

  • 流程架构 Process architecture
  • 自组织 Self-organization
  • 社会学和复杂系统理论 Sociology and complexity science
  • 系统性事故 System accident
  • 系统动力学 System dynamics
  • 系统等效性 System equivalence
  • 系统理论 Systems theory
    • 人类学系统论 System theory in anthropology
  • 波动性、不确定性、复杂性、模糊性（VUCA) Volatility, uncertainty, complexity
    and ambiguity

进一步阅读

外部链接

参考文献

  1. ↑ Bar-Yam (2014) "General Features of Complex Systems".Yaneer, Encyclopedia of Life Support Systems. Retrieved 16 September.
  2. ↑ Daniel Dennett (1995), Darwin's Dangerous Idea, Penguin Books, London, ISBN 978-0-14-016734-4, ISBN 0-14-016734-X
  3. ↑ On the ‘complexity turn’ in planning: An adaptive rationale to navigate spaces and times of uncertainty 关于规划中的“复杂性转向” : 一个适应性的理论基础，用于导航不确定性的空间和时间。
  4. ↑ Alan Randall (2011). Risk and Precaution. Cambridge University Press. ISBN 9781139494793.
  5. ↑ S. V. Buldyrev; R. Parshani; G. Paul; H. E. Stanley; S. Havlin (2010). "Catastrophic cascade of failures in interdependent networks". Nature. 464 (7291): 1025–8. arXiv:0907.1182. Bibcode:2010Natur.464.1025B. doi:10.1038/nature08932. PMID 20393559
  6. ↑ Berezin, Yehiel; Bashan, Amir; Danziger, Michael M.; Li, Daqing; Havlin, Shlomo (2015). "Localized attacks on spatially embedded networks with dependencies". Scientific Reports. 5 (1): 8934. Bibcode:2015NatSR...5E8934B. doi:10.1038/srep08934. ISSN 2045-2322. PMC 4355725. PMID 25757572
  7. ↑ 7.0 7.1 Majdandzic, Antonio; Podobnik, Boris; Buldyrev, Sergey V.; Kenett, Dror Y.; Havlin, Shlomo; Eugene Stanley, H. (2013). "Spontaneous recovery in dynamical networks". Nature Physics. 10 (1): 34–38. Bibcode:2014NatPh..10...34M. doi:10.1038/nphys2819. ISSN 1745-2473.
  8. ↑ Lever, J. Jelle; Leemput, Ingrid A.; Weinans, Els; Quax, Rick; Dakos, Vasilis; Nes, Egbert H.; Bascompte, Jordi; Scheffer, Marten (10 November 2019). "Foreseeing the future of mutualistic communities beyond collapse". Ecology Letters. doi:10.1111/ele.13401. PMID 31707763.
  9. ↑ 9.0 9.1 Majdandzic, Antonio; Braunstein, Lidia A.; Curme, Chester; Vodenska, Irena; Levy-Carciente, Sary; Eugene Stanley, H.; Havlin, Shlomo (2016). "Multiple tipping points and optimal repairing in interacting networks". Nature Communications. 7: 10850. arXiv:1502.00244. Bibcode:2016NatCo...710850M. doi:10.1038/ncomms10850. ISSN 2041-1723. PMC 4773515. PMID 26926803.
  10. ↑ Bascompte, J.; Jordano, P.; Melian, C. J.; Olesen, J. M. (24 July 2003). "The nested assembly of plant-animal mutualistic networks". Proceedings of the National Academy of Sciences. 100 (16): 9383–9387. doi:10.1073/pnas.1633576100. PMC 170927. PMID 12881488.
  11. ↑ Saavedra, Serguei; Reed-Tsochas, Felix; Uzzi, Brian (January 2009). "A simple model of bipartite cooperation for ecological and organizational networks". Nature. 457 (7228): 463–466. doi:10.1038/nature07532. ISSN 1476-4687. PMID 19052545.
  12. ↑ Bastolla, Ugo; Fortuna, Miguel A.; Pascual-García, Alberto; Ferrera, Antonio; Luque, Bartolo; Bascompte, Jordi (April 2009). "The architecture of mutualistic networks minimizes competition and increases biodiversity". Nature. 458 (7241): 1018–1020. doi:10.1038/nature07950. ISSN 1476-4687. PMID 19396144.
  13. ↑ Lever, J. Jelle; Nes, Egbert H. van; Scheffer, Marten; Bascompte, Jordi (2014). "The sudden collapse of pollinator communities". Ecology Letters. 17 (3): 350–359. doi:10.1111/ele.12236. hdl:10261/91808. ISSN 1461-0248. PMID 24386999.
  14. ↑ A. L. Barab´asi, R. Albert (2002). "Statistical mechanics of complex networks". Reviews of Modern Physics. 74 (1): 47–94. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. CiteSeerX 10.1.1.242.4753. doi:10.1103/RevModPhys.74.47
  15. ↑ M. Newman (2010). Networks: An Introduction. Oxford University Press. ISBN 978-0-19-920665-0.
  16. ↑ 16.0 16.1 Reuven Cohen, Shlomo Havlin (2010).Complex Networks: Structure, Robustness and Function. Cambridge University Press. ISBN 978-0-521-84156-6.
  17. ↑ Castellani, Brian, 2018, Map of the Complexity Sciences Art & Science Factory (expandable version)
  18. ↑ History of Complex Systems Archived 2007-11-23 at the 2007-11-23Wayback Machine
  19. ↑ Ferguson, Adam (1767). An Essay on the History of Civil Society. London: T. Cadell. Part the Third, Section II, p. 205.
  20. ↑ Friedrich Hayek, "The Results of Human Action but Not of Human Design" in New Studies in Philosophy, Politics, Economics, Chicago: University of Chicago Press, 1978, pp. 96–105.
  21. ↑ Bruce J. Caldwell, Popper and Hayek:Who influenced whom? Archived 2018-12-11 at the Wayback Machine, Karl Popper 2002 Centenary Congress, 2002.
  22. ↑ Friedrich von Hayek, The Sensory Order: An Inquiry into the Foundations of Theoretical Psychology, The University of Chicago Press, 1952.
  23. ↑ Vemuri, V. (1978). Modeling of Complex Systems: An Introduction. New York: Academic Press. ISBN 978-0127165509.
  24. ↑ Ledford, H (2015). "How to solve the world's biggest problems". Nature. 525 (7569): 308–311. Bibcode:2015Natur.525..308L. doi:10.1038/525308a. PMID 26381968.
  25. ↑ "History | Santa Fe Institute". www.santafe.edu. Retrieved 2018-05-17.
  26. ↑ Waldrop, M. M. (1993). Complexity: The emerging science at the edge of order and chaos. Simon and Schuster.
  27. ↑ CSIS paper: "Organizing for a Complex World: The Way Ahead
  28. ↑ Forsman, Jonas; Moll, Rachel; Linder, Cedric (2014). "Extending the theoretical framing for physics education research: An illustrative application of complexity science". Physical Review Special Topics: Physics Education Research. 10 (2): 020122. Bibcode:2014PRPER..10b0122F. doi:10.1103/PhysRevSTPER.10.020122. http://hdl.handle.net/10613/2583.
  29. ↑ ["Reason Magazine - The Road from Serfdom" "Reason Magazine - The Road from Serfdom"]. Archived from the original on 2007-03-10. Retrieved 2017-09-22.
  30. ↑ Friedrich August von Hayek - Prize Lecture
  31. ↑ Hayles, N. K. (1991). Chaos Bound: Orderly Disorder in Contemporary Literature and Science. Cornell University Press, Ithaca, NY.
  32. ↑ Prigogine, I. (1997). The End of Certainty, The Free Press, New York.
  33. ↑ See also D. Carfì (2008). "Superpositions in Prigogine approach to irreversibility". AAPP: Physical, Mathematical, and Natural Sciences. 86 (1): 1–13.
  34. ↑ 34.0 34.1 Cilliers, P. (1998). Complexity and Postmodernism: Understanding Complex Systems, Routledge, London.
  35. ↑ Per Bak (1996). How Nature Works: The Science of Self-Organized Criticality, Copernicus, New York, U.S.c
  36. ↑ Colander, D. (2000). The Complexity Vision and the Teaching of Economics, E. Elgar, Northampton, Massachusetts.
  37. ↑ Buchanan, M. (2000). Ubiquity : Why catastrophes happen, three river press, New-York.
  38. ↑ Gell-Mann, M. (1995). What is Complexity? Complexity 1/1, 16-19
  39. ↑ Dorogovtsev, S.N.; Mendes, J.F.F. (2003). Evolution of Networks. Adv. Phys. 51. p. 1079. arXiv:cond-mat/0106144. doi:10.1093/acprof:oso/9780198515906.001.0001. ISBN 9780198515906.
  40. ↑ Fortunato, Santo (2011). "Reuven Cohen and Shlomo Havlin: Complex Networks". Journal of Statistical Physics. 142 (3): 640–641. Bibcode:2011JSP...142..640F. doi:10.1007/s10955-011-0129-7. ISSN 0022-4715.
  41. ↑ Newman, Mark (2010).Networks. doi:10.1093/acprof:oso/9780199206650.001.0001. ISBN 9780199206650.
  42. ↑ Cohen, Reuven; Erez, Keren; ben-Avraham, Daniel; Havlin, Shlomo (2001). "Cohen, Erez, ben-Avraham, and Havlin Reply". Physical Review Letters. 87 (21): 219802. Bibcode:2001PhRvL..87u9802C. doi:10.1103/PhysRevLett.87.219802. ISSN 0031-9007.
  43. ↑ Barrat, A.; Barthelemy, M.; Pastor-Satorras, R.; Vespignani, A. (2004). "The architecture of complex weighted networks". Proceedings of the National Academy of Sciences. 101 (11): 3747–3752. arXiv:cond-mat/0311416. Bibcode:2004PNAS..101.3747B. doi:10.1073/pnas.0400087101. ISSN 0027-8424. PMC 374315. PMID 15007165
  44. ↑ Yamasaki, K.; Gozolchiani, A.; Havlin, S. (2008). "Climate Networks around the Globe are Significantly Affected by El Niño". Physical Review Letters. 100 (22): 228501. Bibcode:2008PhRvL.100v8501Y. doi:10.1103/PhysRevLett.100.228501. ISSN 0031-9007. PMID 18643467.
  45. ↑ Gao, Jianxi; Buldyrev, Sergey V.; Stanley, H. Eugene; Havlin, Shlomo (2011)."Networks formed from interdependent networks" (PDF). Nature Physics. 8 (1): 40–48. Bibcode:2012NatPh...8...40G. CiteSeerX 10.1.1.379.8214. doi:10.1038/nphys2180. ISSN 1745-2473.
  46. ↑ Li, Daqing; Fu, Bowen; Wang, Yunpeng; Lu, Guangquan; Berezin, Yehiel; Stanley, H. Eugene; Havlin, Shlomo (2015-01-20). "Percolation transition in dynamical traffic network with evolving critical bottlenecks". Proceedings of the National Academy of Sciences. 112 (3): 669–672. Bibcode:2015PNAS..112..669L. doi:10.1073/pnas.1419185112. ISSN 0027-8424. PMC 4311803. PMID 25552558
  47. ↑ Limiao Zhang, Guanwen Zeng; Daqing Li, Hai-Jun Huang; H Eugene Stanley, Shlomo Havlin (2019). "Scale-free resilience of real traffic jams". Proceedings of the National Academy of Sciences. 116 (18): 8673–8678. arXiv:1804.11047. Bibcode:2019PNAS..116.8673Z. doi:10.1073/pnas.1814982116. PMC 6500150. PMID 30979803
  48. ↑ Battiston, Stefano; Caldarelli, Guido; May, Robert M.; Roukny, tarik; Stiglitz, Joseph E. (2016-09-06). "The price of complexity in financial networks". Proceedings of the National Academy of Sciences. 113 (36): 10031–10036. Bibcode:2016PNAS..11310031B. doi:10.1073/pnas.1521573113. PMC 5018742. PMID 27555583.
  49. ↑ Wenliang Wang (2015). Pooling Game Theory and Public Pension Plan. ISBN 978-1507658246. Chapter 4.

编者推荐

推荐一下国内网站上就能访问到的学习资源：

电子书《复杂》下载 by <美>梅拉妮•米歇尔（Melanie Mitchell）
系统科学导引（一）：概论部分
系统科学导引（二）：数学部分
系统科学导引（三）：物理部分
系统科学导引（四）：量子力学
  • 复杂系统科普入门： 复杂 Complexity 梅拉妮·米歇尔 Melanie Mitchell
梅拉妮是道格拉斯·侯世达 Douglas Hofstadter的学生，目前在波特兰大学执教。主要工作方向是类比推理、复杂系统、基因算法与元胞自动机。《复杂》自2009出版后，一路好评，豆瓣评分9分。从起源、演进、定义、度量几个方面介绍什么是复杂系统。

--- 本中文词条由wanting参与编译，刘佩佩审校，薄荷编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=复杂系统_Complex_Systems&oldid=2527”