“复杂性”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
第1行： 第1行：
−
此词条暂由彩云小译翻译，翻译字数共2038，未经人工整理和审校，带来阅读不便，请见谅。
+
The '''complexity''' of a physical system or a dynamical process expresses the degree to which components engage in organized structured interactions.  High complexity is achieved in systems that exhibit a mixture of order and disorder (randomness and regularity) and that have a high capacity to generate emergent phenomena.
  
 +
物理系统或动态过程的'''复杂性'''表达了组件参与有组织的结构化交互的程度。高度复杂的系统实现了有序和无序(规律性和随机性)的混合，并有很高的可能产生涌现现象。
  
−
'''Complexity''' characterises the behaviour of a [[system]] or [[model (disambiguation)|model]] whose components [[interaction|interact]] in multiple ways and follow local rules, meaning there is no reasonable higher instruction to define the various possible interactions.
 
  
−
Complexity characterises the behaviour of a system or model whose components interact in multiple ways and follow local rules, meaning there is no reasonable higher instruction to define the various possible interactions.
+
==各学科中的复杂性==
  
−
复杂性描述了一个系统或模型的行为，其组件以多种方式交互并遵循局部规则，这意味着没有更高级（全局）指令来定义各种可能的交互。.<ref name="steven">{{cite book
+
Despite the importance and ubiquity of the concept of complexity in modern science and society, no general and widely accepted means of measuring the complexity of a physical object, system, or process currently exists. The lack of any general measure may reflect the nascent stage of our understanding of complex systems, which still lacks a general unified framework that cuts across all natural and social sciences.  While a general measure has remained elusive until now, there is a broad spectrum of measures of complexity that apply to specific types of systems or problem domains.  The justification for each of these measures often rests on their ability to produce intuitively correct values at the extremes of the complexity spectrum. Despite the heterogeneous approaches taken to defining and measuring complexity, the belief persists that there are properties common to all complex systems, and new proposals are continually being produced and tested by an interdisciplinary community of physicists, biologists, mathematicians, computer scientists, economists and social theorists.
−
| last = Johnson
 
−
| first = Steven
 
−
| title = Emergence: The Connected Lives of Ants, Brains, Cities
 
−
| publisher = Scribner
 
−
| year = 2001
 
−
| location = New York
 
−
| url = https://books.google.com/books?id=Au_tLkCwExQC
 
−
| page = 19
 
−
| isbn = 978-3411040742}}
 
−
</ref>
 
  
 +
尽管复杂性的概念在现代科学和社会中非常重要和普遍存在，但目前还没有一种普遍的、广泛接受的方法来衡量一个物理对象、系统或过程的复杂性。缺乏普遍的衡量标准，可能反映了我们对复杂系统的理解处于初始阶段，缺乏一个贯穿所有自然科学和社会科学的普遍的统一框架。虽然到目前为止，一般性的衡量标准仍然难以捉摸，但是，我们拥有许多适用于具体类型的系统或问题领域的复杂性衡量标准。尽管在定义和测量复杂性方面存在了各种不同的方法，但有一种信念仍然坚持认为所有复杂系统都有共同的特性，而且新的定义和度量正在不断地被一个由物理学家、生物学家、数学家、计算机科学家、经济学家和社会理论家组成的跨学科团体提出和检验。
  
−
The term is generally used to characterize something with many parts where those parts interact with each other in multiple ways, culminating in a higher order of emergence greater than the sum of its parts. The study of these complex linkages at various scales is the main goal of complex systems theory.
 
  
−
这个术语通常用来描述具有许多组成部分的事物，其中这些部分以多种方式相互作用，最终以大于其各部分之和的更高级别出现。在不同尺度上研究这些复杂的结构是复杂系统理论的主要目标。
+
This article deals with complexity from an information-theoretical perspective.  A treatment of complexity from the perspective of dynamical systems can be found in another article ([[Complex Systems]]).
  
 +
本文从信息论的角度探讨复杂性问题。读者还可以从[[复杂系统|系统论]]的角度出发理解复杂性。
  
−
[[Science]] {{as of | 2010 | lc = on}} takes a number of approaches to characterizing complexity; Zayed ''et al.''<ref>
 
−
J. M. Zayed, N. Nouvel, U. Rauwald, O. A. Scherman. ''Chemical Complexity – supramolecular self-assembly of synthetic and biological building blocks in water''. Chemical Society Reviews, 2010, 39, 2806–2816 http://pubs.rsc.org/en/Content/ArticleLanding/2010/CS/b922348g
 
−
</ref>reflect many of these. Neil Johnson states that "even among scientists, there is no unique definition of complexity – and the scientific notion has traditionally been conveyed using particular examples..."  Ultimately Johnson adopts the definition of "complexity science" as "the study of the phenomena which emerge from a collection of interacting objects".
 
  
−
科学里有许多种刻画复杂性的方法，比如 Zayed 的书中<ref>J. M. Zayed, N. Nouvel, U. Rauwald, O. A. Scherman. ''Chemical Complexity – supramolecular self-assembly of synthetic and biological building blocks in water''. Chemical Society Reviews, 2010, 39, 2806–2816 http://pubs.rsc.org/en/Content/ArticleLanding/2010/CS/b922348g
+
==复杂性的一般特征==
−
</ref>就给出许多案例。Neil Johnson 指出：“即使在科学家群体中，也没有关于复杂性的独特定义——传统上，关于复杂性的科学观念也是通过特定的例子来表达的... ... ”最终，Johnson 采用了“复杂性科学”的定义，即“研究从一系列相互作用的物体中产生的现象”。
 
  
 +
Quantitative or analytic definitions of complexity often disagree about the precise formulation, or indeed even the formal framework within which complexity is to be defined.  Yet, there is an informal notion of complexity based upon some of the ingredients that are shared by most if not all complex systems and processes.  Herbert Simon was among the first to discuss the nature and architecture of complex systems (Simon, 1981) and he suggested to define complex systems as those that are “made up of a large number of parts that have many interactions.”  Simon goes on to note that “in such systems the whole is more than the sum of the parts in the […] sense that, given the properties of the parts and the laws of their interaction, it is not a trivial matter to infer the properties of the whole.”
  
−
== 综述 ==
+
复杂性的定量或分析学（analytic）定义往往不同意精确的表述，甚至不同意定义复杂性的正式框架。然而，有一种非正式的复杂性概念，它基于大多数(如果不是所有的话)复杂系统和过程所共有的一些要素。赫伯特 · 西蒙是最早讨论复杂系统的性质和结构的人之一(Simon，1981) ，他建议将复杂系统定义为那些“由大量具有许多相互作用的部分组成”的系统。西蒙接着指出，“在这样的系统中，整体不仅仅在[ ... ]的意义上大于各部分之和，考虑到各部分的性质及其相互作用的规律，推断整体的性质不是一件容易事。”
  
−
Definitions of complexity often depend on the concept of a "system" – a set of parts or elements that have relationships among them differentiated from relationships with other elements outside the relational regime. Many definitions tend to postulate or assume that complexity expresses a condition of numerous elements in a system and numerous forms of relationships among the elements. However, what one sees as complex and what one sees as simple is relative and changes with time.
 
  
−
复杂性的定义往往依赖于“系统”的概念，即一系列组成部分或组成要素之间的关系。许多定义倾向于认为复杂性表达了系统中的众多元素和元素之间的众多关系形式。然而，人们所认为的复杂和简单是相对的，并且随着时间的推移而变化。
+
'''Components.'''  Many complex systems can be decomposed into components (elements, units) that are structurally distinct, and may function as individuals, generating some form of local behavior, activity or dynamics.  Components of complex systems may themselves be decomposable into subcomponents, resulting in systems that are complex at multiple levels of organization, forming hierarchies of nearly, but not completely decomposable components.
  
 +
'''组分''' 许多复杂的系统可以分解成结构上不同的组成部分(组件、元素、单元) ，且它们可以作为个体发挥作用，产生某种形式的局部行为、活动或动态。复杂系统的组件本身可以分解为子组件，导致系统在多层次的组织中是复杂的，形成（不完全）可分解的组件层次结构。
  
  
−
Warren Weaver posited in 1948 two forms of complexity: disorganized complexity, and organized complexity.
+
'''Interactions.'''  Components of complex systems engage in dynamic interactions, resulting in integration or binding of these components across space and time into an organized whole.  Interactions often modulate the individual actions of the components, thus altering their local functionality by relaying global context.  In many complex systems, interactions between subsets of components are mediated by some form of communication paths or connections.  Such structured interactions are often sparse, i.e. only a small subset of all possible interactions is actually realized within the system.  The specific patterns of these interactions are crucial in determining how the system functions as a whole.  Some interactions between components may be strong, in the sense that they possess great efficacy with respect to individual components.  Other interactions may be considered weak, as their effects are limited in size or sporadic across time.  Both, strong and weak interactions can have significant effects on the system as a whole.
  
−
沃伦 · 韦弗在1948年提出了复杂性的两种形式: '''无组织的复杂性 disorganized complexity'''和'''有组织的复杂性 organized complexity'''。<ref name=Weaver>{{Cite journal
+
'''交互''' 复杂系统的组成部分进行动态交互，导致这些组成部分跨空间和时间整合成一个有组织的整体。交互通常能调节组件的单个动作，从而通过'''中继全局上下文 relaying global context''' 改变其局部功能。在许多复杂系统中，组件子集之间的交互是通过某种形式的通信路径或连接进行的。这样的结构化交互通常是稀疏的，也就是说，所有可能的交互中只有一小部分是在系统中实现的。这些相互作用的具体模式对于确定系统作为一个整体如何运作至关重要。组件之间的某些相互作用可能很强，因为它们对于单个组件具有很大的效力。其他相互作用可能被认为是弱的，因为他们的影响范围或时间是有限的。无论是强相互作用还是弱相互作用，都能对整个系统产生重大影响。
−
  | last = Weaver
 
−
  | first = Warren
 
−
  | title = Science and Complexity
 
−
  | journal = American Scientist
 
−
  | volume = 36
 
−
  | pages = 536–44
 
−
  | year = 1948
 
−
  | url = http://people.physics.anu.edu.au/~tas110/Teaching/Lectures/L1/Material/WEAVER1947.pdf
 
−
  | pmid = 18882675
 
−
  | issue = 4
 
−
  | access-date = 2007-11-21}}
 
−
</ref>
 
  
  
−
Phenomena of 'disorganized complexity' are treated using probability theory and statistical mechanics, while 'organized complexity' deals with phenomena that escape such approaches and confront "dealing simultaneously with a sizable number of factors which are interrelated into an organic whole".
+
'''Emergence.''' Interactions between components in integrated systems often generate phenomena, functions, or effects that cannot be trivially reduced to properties of the components alone.  Instead these functions emerge as a result of structured interactions and are properties of the system as a whole.  In many cases, even a detailed and complete examination of the individual components will fail to predict the range of emergent processes that these components are capable of if allowed to interact as part of a system.  In turn, dissection of an integrated system into components and interactions generally results in a loss of the emergent process.  
  
−
“无组织的复杂性”现象可以用概率论和统计力学来处理，而‘有组织的复杂性’则要处理不适用这种方法的现象，面对的主要问题是“同时处理大规模的相关因素，且这些因素相互关联，形成一个有机的整体”。
+
In summary, systems with numerous components capable of structured interactions that generate emergent phenomena may be called complex.  The observation of complex systems poses many challenges, as an observer needs simultaneously to record states and state transitions of many components and interactions.  Such observations require that choices be made concerning the definition of states, state space and time resolution.  How states are defined and measured can impact other derived measures such as those of system complexity.
  
 +
[[Image:complexity_figure1.jpg|thumb|300px|left|F1|Complexity as a mixture of order and disorder. Drawn after Huberman and Hogg (1986).]]
  
−
The approaches that embody concepts of systems, multiple elements, multiple relational regimes, and state spaces might be summarized as implying that complexity arises from the number of distinguishable relational regimes (and their associated state spaces) in a defined system.
+
==复杂性的度量==
  
−
体现系统、多元素、多关系体系和状态空间概念的方法可以概括为: 复杂性来自于一个已定义系统中可区分的关系体系(及其相关的状态空间)的数量。
+
Measures of complexity allow different systems to be compared to each other by applying a common metric.  This is especially meaningful for systems that are structurally or functionally related.  Differences in complexity among such related systems may reveal features of their organization that promote complexity.
  
 +
Some measures of complexity are algorithmic in nature and attempt to identify a minimal description length.  For these measures complexity applies to a description, not the system or process per se.  Other measures of complexity take into account the time evolution of a system and often build on the theoretical foundations of statistical information theory.
  
−
== Disorganized vs. organized ==
+
Most extant complexity measures can be grouped into two main categories. Members of the first category (algorithmic information content and logical depth) all capture the randomness, information content or description length of a system or process, with random processes possessing the highest complexity since they most resist compression.  The second category (including statistical complexity, physical complexity and neural complexity) conceptualizes complexity as distinct from randomness.  Here, complex systems are those that possess a high amount of structure or information, often across multiple temporal and spatial scales.  Within this category of measures, highly complex systems are positioned somewhere between systems that are highly ordered (regular) or highly disordered (random). <figref>Complexity_figure1.jpg</figref> shows a schematic diagram of the shape of such measures, however, it should be emphasized again that a generally accepted quantitative expression linking complexity and disorder does not currently exist.
−
One of the problems in addressing complexity issues has been formalizing the intuitive conceptual distinction between the large number of variances in relationships extant in random collections, and the sometimes large, but smaller, number of relationships between elements in systems where constraints (related to correlation of otherwise independent elements) simultaneously reduce the variations from element independence and create distinguishable regimes of more-uniform, or correlated, relationships, or interactions.
 
  
−
解决复杂性问题的一个问题是将随机集合中现存的大量关系变量与系统中有时较大但较小的元素之间的关系(与其他独立元素的相关性有关)同时减少了元素独立性的变量，并创造了更加统一或相关的关系或相互作用的可区分的制度之间的直观概念区分形式化。
+
==复杂与随机==
  
−
Weaver perceived and addressed this problem, in at least a preliminary way, in drawing a distinction between "disorganized complexity" and "organized complexity".
+
Algorithmic information content was defined (Kolmogorov, 1965; Chaitin, 1977) as the amount of information contained in a string of symbols given by the length of the shortest computer program that generates the string.  Highly regular, periodic or monotonic strings may be computed by programs that are short and thus contain little information, while random strings require a program that is as long as the string itself, thus resulting in high (maximal) information content.  Algorithmic information content (AIC) captures the amount of randomness of symbol strings, but seems ill suited for applications to biological or neural systems and, in addition, has the inconvenient property of being uncomputable.  For further discussion see [[algorithmic information theory]].
  
−
在区分“无组织的复杂性”和“有组织的复杂性”时，编织者至少以一种初步的方式察觉并解决了这个问题。
+
Logical Depth (Bennett, 1988) is related to AIC and draws additionally on computational complexity defined as the minimal amount of computational resources (time, memory) needed to solve a given class of problem.  Complexity as logical depth refers mainly to the running time of the shortest program capable of generating a given string or pattern.  Similarly to AIC, complexity as logical depth is a measure of a generative process and does not apply directly to an actually existing physical system or dynamical process.  Computing logical depth requires knowing the shortest computer program, thus the measure is subject to the same fundamental limitation as AIC.
  
−
In Weaver's view, disorganized complexity results from the particular system having a very large number of parts, say millions of parts, or many more. Though the interactions of the parts in a "disorganized complexity" situation can be seen as largely random, the properties of the system as a whole can be understood by using probability and statistical methods.
+
Effective measure complexity (Grassberger, 1986) quantifies the complexity of a sequence by the amount of information contained in a given part of the sequence that is needed to predict the next symbol.  Effective measure complexity can capture structure in sequences that range over multiple scales and it is related to the extensivity of entropy (see below).
  
−
在韦弗看来，无组织的复杂性是由于特定系统具有非常多的部件，比如数百万个部件，或者更多。虽然在“无组织复杂性”的情况下，各部分之间的相互作用可以看作是很大程度上的随机性，但是系统作为一个整体的性质可以通过使用概率和统计方法来理解。
+
Thermodynamic depth (Lloyd and Pagels, 1988) relates the entropy of a system to the number of possible historical paths that led to its observed state, with “deep” systems being all those that are “hard to build”, whose final state carries much information about the history leading up to it.  The emphasis on how a system comes to be, its generative history, identifies thermodynamic depth as a complementary measure to logical depth.  While thermodynamic depth has the advantage of being empirically calculable, problems with the definition of system states have been noted (Crutchfield and Shalizi, 1999).  Although aimed at distinguishing complex systems as different from random ones, its formalism essentially captures the amount of randomness created by a generative process, and does not differentiate regular from random systems.
  
 +
==作为结构和信息的复杂性==
  
−
A prime example of disorganized complexity is a gas in a container, with the gas molecules as the parts. Some would suggest that a system of disorganized complexity may be compared with the (relative) simplicity of planetary orbits – the latter can be predicted by applying Newton's laws of motion. Of course, most real-world systems, including planetary orbits, eventually become theoretically unpredictable even using Newtonian dynamics; as discovered by modern chaos theory.
+
A simple way of quantifying complexity on a structural basis would be to count the number of components and/or interactions within a system.  An examination of the number of structural parts (McShea, 1996) and functional behaviors of organisms across evolution demonstrates that these measures increase over time, a finding that contributes to the ongoing debate over whether complexity grows as a result of natural selection.  However, numerosity alone may only be an indicator of complicatedness, but not necessarily of complexity. Large and highly coupled systems may not be more complex than those that are smaller and less coupled.  For example, a very large system that is fully connected can be described in a compact manner and may tend to generate uniform behavior, while the description of a smaller but more heterogeneous system may be less compressible and its behavior may be more differentiated.
  
−
无组织复杂性的一个典型例子是一个容器中的气体，以气体分子为部件。有些人认为，一个无组织的复杂系统可以与行星轨道的(相对)简单性相比较——后者可以通过应用牛顿运动定律来预测。当然，大多数真实世界的系统，包括行星轨道，最终在理论上变得不可预测，即使使用牛顿动力学; 正如现代混沌理论所发现的那样。
+
Effective complexity (Gell-Mann, 1995) measures the minimal description length of a system’s regularities.  As such, this measure is related to AIC, but it attempts to distinguish regular features from random or incidental ones and therefore belongs within the family of complexity measures that aim at capturing how much structure a system contains. The separation of regular features from random ones may be difficult for any given empirical system, and it may crucially depend on criteria supplied by an external observer.
  
 +
Physical complexity (Adami and Cerf, 2000) is related to effective complexity and is designed to estimate the complexity of any sequence of symbols that is about a physical world or environment.  As such the measure is particularly useful when applied to biological systems.  It is defined as the Kolmogorov complexity (AIC) that is shared between a sequence of symbols (such as a genome) and some description of the environment in which that sequence has meaning (such as an ecological niche).  Since the Kolmogorov complexity is not computable, neither is the physical complexity.  However, the average physical complexity of an ensemble of sequences (e.g. the set of genomes of an entire population of organisms) can be approximated by the mutual information between the ensembles of sequences (genomes) and their environment (ecology).  Experiments conducted in a digital ecology (Adami, 2002) demonstrated that the mutual information between self-replicating genomes and their environment increased along evolutionary time.  Physical complexity has also been used to estimate the complexity of biomolecules.  The structural and functional complexity of a set of RNA molecules were shown to positively correlate with physical complexity (Carothers et al., 2004), indicating a possible link between functional capacities of evolved molecular structures and the amount of information they encode.
  
−
Organized complexity, in Weaver's view, resides in nothing else than the non-random, or correlated, interaction between the parts. These correlated relationships create a differentiated structure that can, as a system, interact with other systems. The coordinated system manifests properties not carried or dictated by individual parts. The organized aspect of this form of complexity vis-a-vis to other systems than the subject system can be said to "emerge," without any "guiding hand".
+
Statistical complexity (Crutchfield and Young, 1989) is a component of a broader theoretic framework known as computational mechanics, and can be calculated directly from empirical data.  To calculate the statistical complexity, each point in the time series is mapped to a corresponding symbol according to some partitioning scheme, so that the raw data is now a stream of consecutive symbols.  The symbol sequences are then clustered into causal states according to the following rule: two symbol sequences (i.e. histories of the dynamics) are contained in the same causal state if the conditional probability of any future symbol is identical for these two histories.  In other words, two symbol sequences are considered to be the same if, on average, they predict the same distribution of future dynamics. Once these causal states have been identified, the transition probabilities between causal states can be extracted from the data, and the long-run probability distribution over all causal states can be calculated. The statistical complexity is then defined as the Shannon entropy of this distribution over causal states.  Statistical complexity can be calculated analytically for abstract systems such as the logistic map, cellular automata and many basic Markov processes, and computational methods for constructing appropriate causal states in real systems, while taxing, exist and have been applied in a variety of contexts.
  
−
在 Weaver 看来，有组织的复杂性仅仅存在于各部分之间的非随机或相关的交互中。这些相互关联的关系创建了一个可以作为一个系统与其他系统交互的差异化结构。协调系统显示的属性不是由单个部分承载或支配的。这种形式的复杂性相对于主体系统以外的其他系统的有组织的方面可以说是“浮现” ，没有任何“指导手”。
+
Predictive information (Bialek et al., 2001), while not in itself a complexity measure, can be used to separate systems into different complexity categories based on the principle of the extensivity of entropy.  Extensivity manifests itself, for example, in systems composed of increasing numbers of homogeneous independent random variables.  The Shannon entropy of such systems will grow linearly with their size.  This linear growth of entropy with system size is known as extensivity.  However, the constituent elements of a complex system are typically inhomogeneous and interdependent, so that as the number of random variables grows the entropy does not always grow linearly.  The manner in which a given system departs from extensivity can be used to characterize its complexity.
  
−
The number of parts does not have to be very large for a particular system to have emergent properties. A system of organized complexity may be understood in its properties (behavior among the properties) through modeling and simulation, particularly modeling and simulation with computers. An example of organized complexity is a city neighborhood as a living mechanism, with the neighborhood people among the system's parts.
+
[[Image:complexity_figure2.jpg|thumb|400px|right|F2|Movie frames from a demonstration model of neural dynamics, consisting of 1600 spontaneously active Wison-Cowan neural mass units arranged on a sphere and coupled by excitatory connections. Three cases are shown: sparse coupling (local connections only), uniform coupling (global connections only), and a mixture of local and global connections (forming a small-world network). Neural complexity (Tononi et al., 1994; Sporns et al., 2000) is high only for the last case.]]
  
−
对于一个具有涌现特性的特定系统来说，部件的数量不一定非常大。一个有组织的复杂系统可以从它的属性(属性之间的行为)来理解，通过建模与模拟，特别是计算机的建模与模拟。有组织的复杂性的一个例子是一个城市邻里作为一个生活机制，与邻里的人在系统的部分。
+
Neural complexity (Tononi et al., 1994), which may be applied to any empirically observed system including brains, is related to the extensivity of a system.  One of its building blocks is integration (also called multi-information), a multivariate extension of mutual information that estimates the total amount of statistical structure within an arbitrarily large system.  Integration is computed as the difference between the sum of the component’s individual entropies and the joint entropy of the system as a whole.  The distribution of integration across multiple spatial scales captures the complexity of the system.  Consider the following three cases (<figref>Complexity_figure2.jpg</figref>).  (1) A system with components that are statistically independent will exhibit globally disordered or random dynamics.  Its joint entropy will be exactly equal to the sum of the component entropies, and system integration will be zero, regardless of which spatial scale of the system is examined.  (2) Any statistical dependence between components will lead to a contraction of the system’s joint entropy relative to the individual entropies, resulting in positive integration.  If the components of a system are highly coupled and exhibit statistical dependencies as well as homogeneous dynamics (i.e. all components behave identically) then estimates of integration across multiple spatial scales of the system will, on average, follow a linear distribution.  (3) If statistical dependencies are inhomogeneous (for example involving groupings of components, modules, or hierarchical patterns) the distribution of integration will deviate from linearity.  The total amount of deviation is the system’s complexity.  The complexity of a random system is zero, while the complexity of a homogeneous coupled (regular) system is very low.  Systems with rich structure and dynamic behavior have high complexity.
  
−
There are generally rules which can be invoked to explain the origin of complexity in a given system.
+
Applied to neural dynamics, complexity as defined by Tononi et al. (1994) was found to be associated with specific patterns of neural connectivity, for example those exhibiting attributes of small-world networks (Sporns et al., 2000).  Descendants of this complexity measure have addressed the matching of systems to an environment as well as their degeneracy, i.e. their capacity to produce functionally equivalent behaviors in different ways.  
  
−
通常有一些规则可以用来解释给定系统中复杂性的起源。
+
==复杂网络==
  
 +
Traditionally, complex systems have been analyzed using tools from nonlinear dynamics and statistical information theory.  Recently, the analytical framework of complex networks has led to a significant reappraisal of commonalities and differences between complex systems found in different scientific domains (Amaral and Ottino, 2004).  A key insight is that network topology, the graph structure of the interactions, places important constraints on the system's dynamics, by directing information flow, creating patterns of coherence between components, and by shaping the emergence of macroscopic system states.  Complexity is highly sensitive to changes in network topology (Sporns et al., 2000).  Changes in connection patterns or strengths may thus serve as modulators of complexity.  The link between network structure and dynamics represents one of the most promising areas of complexity research in the near future.
  
 +
==为什么是复杂性？==
  
−
== Overview ==
+
Why does complexity exist in the first place, especially among biological systems?  A definitive answer to this question remains elusive.  One perspective is based on the evolutionary demands biological systems face.  The evolutionary success of biological structures and organisms depends on their ability to capture information about the environment, be it molecular or ecological.  Biological complexity may then emerge as a result of evolutionary pressure on the effective encoding of structured relationships which support differential survival.
  
−
The source of disorganized complexity is the large number of parts in the system of interest, and the lack of correlation between elements in the system.
+
Another clue may be found in the emerging link between complexity and network structure.  Complexity appears very prominently in systems that combine segregated and heterogeneous components with large-scale integration.  Such systems become more complex as they more efficiently integrate more information, that is, as they become more capable to accommodate both the existence of specialized components that generate information and the existence of structured interactions that bind these components into a coherent whole.  Thus reconciling parts and wholes, complexity may be a necessary manifestation of a fundamental dialectic in nature.
  
−
无组织复杂性的根源是感兴趣系统中的大量部件，以及系统中各要素之间缺乏相关性。
+
==引用==
  
−
Definitions of complexity often depend on the concept of a "[[system]]" – a set of parts or elements that have relationships among them differentiated from relationships with other elements outside the relational regime. Many definitions tend to postulate or assume that complexity expresses a condition of numerous elements in a system and numerous forms of relationships among the elements. However, what one sees as complex and what one sees as simple is relative and changes with time.
+
*Adami, C. (2002) What is complexity?  BioEssays 24, 1085-1094.
  
 +
*Adami, C., Cerf, N.J. (2000) Physical complexity of symbolic sequences.  Physica D 137, 62-69.
  
 +
*Amaral, L.A.N., Ottino, J.M. (2004) Complex networks.  Eur. Phys. J. B 38, 147-162.
  
−
In the case of self-organizing living systems, usefully organized complexity comes from beneficially mutated organisms being selected to survive by their environment for their differential reproductive ability or at least success over inanimate matter or less organized complex organisms. See e.g. Robert Ulanowicz's treatment of ecosystems.
+
*Bennett, C.H. (1988) Logical depth and physical complexity. In: R. Herken (ed.): The Universal Turing Machine. A Half-Century Survey. Pp. 227-257, Oxford: Oxford University Press.  
  
−
就自我组织的生命系统而言，有效组织的复杂性来自于有益的突变生物体，它们被选择在其环境中生存，因为它们具有不同的生殖能力，或者至少在无生命物质或组织较少的复杂生物体上取得成功。参见。罗伯特·尤兰维奇对生态系统的处理。
+
*Bialek, W., Nemenman, I., Tishby, N. (2001) Predictability, complexity, and learning.  Neural Computation 13, 2409-2463.
  
−
[[Warren Weaver]] posited in 1948 two forms of complexity: disorganized complexity, and organized complexity.
+
*Carothers, J.M., Oestreich, S.C., Davis, J.H., and Szostak, J.W. (2004) Informational complexity and functional activity of RNA structures. J. Am. Chem. Soc. 126, 5130–5137.
  
−
Complexity of an object or system is a relative property. For instance, for many functions (problems), such a computational complexity as time of computation is smaller when multitape Turing machines are used than when Turing machines with one tape are used. Random Access Machines allow one to even more decrease time complexity (Greenlaw and Hoover 1998: 226), while inductive Turing machines can decrease even the complexity class of a function, language or set (Burgin 2005). This shows that tools of activity can be an important factor of complexity.
+
*Chaitin, G.J. (1977) Algorithmic information theory.  IBM Journal of Research and Development 21, 350-359. [http://www.cs.auckland.ac.nz/CDMTCS/chaitin/ibm.pdf]
  
−
对象或系统的复杂性是一个相对的属性。例如，对于许多函数(问题)来说，使用多带图灵机比使用单带图灵机的计算复杂度要小。随机存取机器允许一个人甚至更多地降低时间复杂度(Greenlaw 和 Hoover 1998:226) ，而归纳图灵机甚至可以降低函数、语言或集合的复杂度等级(Burgin 2005)。这表明活动工具可以是复杂性的一个重要因素。
+
*Crutchfield, J.P., Young, K. (1989) Inferring statistical complexity.  Phys. Rev. Lett. 63, 105-109.
  
 +
*Crutchfield, J.P., Shalizi, C.R. (1999) Thermodynamic depth of causal states: Objective complexity via minimal representations.  Phys. Rev. E 59, 275-283.
  
−
In several scientific fields, "complexity" has a precise meaning:
+
*Gell-Mann, M. (1995) What is complexity?  Complexity 1, 16-19.
  
−
在一些科学领域，“复杂性”有着精确的含义:
+
*Grassberger, P. (1986) Toward a quantitative theory of self-generated complexity.  Int. J. Theor. Phys. 25, 907-928.
  
 +
*Huberman, B.A., Hogg, T. (1986) Complexity and adaptation.  Physica D 22, 376-384.
  
−
Phenomena of 'disorganized complexity' are treated using probability theory and statistical mechanics, while 'organized complexity' deals with phenomena that escape such approaches and confront "dealing simultaneously with a sizable number of factors which are interrelated into an organic whole".<ref name=Weaver/> Weaver's 1948 paper has influenced subsequent thinking about complexity.<ref>{{cite book
+
*Kolmogorov, A. N. (1965) Three approaches to the quantitative definition of information. Problems of Information Transmission 1, 1-17.
  
 +
*Lloyd, S., Pagels, H. (1988) Complexity as thermodynamic depth.  Annals of Physics 188, 186-213.
  
−
Other fields introduce less precisely defined notions of complexity:
+
*McShea, D.W. (1995) Metazoan complexity and evolution: Is there a trend?  Evolution 50, 477-492.
  
−
其他领域则引入了定义不那么精确的复杂性概念:
+
*Simon, H.A. (1981) The Sciences of the Artificial.  MIT Press: Cambridge.
  
 +
*Sporns, O., Tononi, G., Edelman, G.M. (2000) Theoretical neuroanatomy: Relating anatomical and functional connectivity in graphs and cortical connection matrices.  Cereb. Cortex 10, 127-141.
  
−
While this has led some fields to come up with specific definitions of complexity, there is a more recent movement to regroup observations from different fields to study complexity in itself, whether it appears in anthills, human brains, or stock markets, social systems. One such interdisciplinary group of fields is relational order theories.
+
*Tononi, G., Sporns, O., Edelman, G.M. (1994) A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. U.S.A. 91, 5033-5037.
  
−
虽然这已经导致一些领域提出了复杂性的具体定义，但是最近有一种运动重新组合来自不同领域的观察结果来研究复杂性本身，无论它是出现在蚁丘、人类大脑，还是股票市场、社会系统。其中一个跨学科的领域就是关系秩序理论。
+
<!-- Authors, please check this list and remove any references that are irrelevant. This list is generated automatically to reflect the links from your article to other accepted articles in Scholarpedia. -->
  
 +
<b>Scholarpedia内部引用</b>
  
 +
* Marcus Hutter (2007) [[Algorithmic information theory]]. Scholarpedia, 2(3):2519.
 +
* Valentino Braitenberg (2007) [[Brain]]. Scholarpedia, 2(11):2918.
 +
* Gregoire Nicolis and Catherine Rouvas-Nicolis (2007) [[Complex systems]]. Scholarpedia, 2(11):1473.
 +
* James Meiss (2007) [[Dynamical systems]]. Scholarpedia, 2(2):1629.
 +
* Tomasz Downarowicz (2007) [[Entropy]]. Scholarpedia, 2(11):3901.
 +
* Arkady Pikovsky and Michael Rosenblum (2007) [[Synchronization]]. Scholarpedia, 2(12):1459.
  
 +
==外部链接==
  
−
The behavior of a complex system is often said to be due to emergence and self-organization. Chaos theory has investigated the sensitivity of systems to variations in initial conditions as one cause of complex behaviour.
+
*[http://www.indiana.edu/~cortex Author 的主页]
−
 
+
*[http://cse.ucdavis.edu/~chaos/index.html Jim Crutchfield  的主页]
−
一个复杂系统的行为通常被认为是由于涌现和自我组织。混沌理论研究了系统对初始条件变化的敏感性，这是导致复杂行为的原因之一。
+
*[http://meche.mit.edu/people/faculty/index.html?id=55 Seth Lloyd 的主页]
−
 
+
*[http://faculty.kgi.edu/adami/ Chris Adami  的主页]
−
The approaches that embody concepts of systems, multiple elements, multiple relational regimes, and state spaces might be summarized as implying that complexity arises from the number of distinguishable relational regimes (and their associated state spaces) in a defined system.
+
*[http://fds.duke.edu/db/aas/Biology/dmcshea Dan McShea  的主页]
−
 
+
*[http://tononi.psychiatry.wisc.edu/ Giulio Tononi  的主页]
−
 
+
*[http://www.indiana.edu/~cortex/complexity_movie.wmv 一段展示图2中连接性和动力学的视频]
−
 
 
−
Some definitions relate to the algorithmic basis for the expression of a complex phenomenon or model or mathematical expression, as later set out herein.
 
−
 
 
−
Recent developments around artificial life, evolutionary computation and genetic algorithms have led to an increasing emphasis on complexity and complex adaptive systems.
 
−
 
 
−
最近围绕人工生命、进化计算和遗传算法的发展使人们越来越重视复杂性和复杂适应系统。
 
−
 
 
−
 
 
−
 
 
−
== Disorganized vs. organized ==
 
−
 
 
−
One of the problems in addressing complexity issues has been formalizing the intuitive conceptual distinction between the large number of variances in relationships extant in random collections, and the sometimes large, but smaller, number of relationships between elements in systems where constraints (related to correlation of otherwise independent elements) simultaneously reduce the variations from element independence and create distinguishable regimes of more-uniform, or correlated, relationships, or interactions.
 
−
 
 
−
In social science, the study on the emergence of macro-properties from the micro-properties, also known as macro-micro view in sociology. The topic is commonly recognized as social complexity that is often related to the use of computer simulation in social science, i.e.: computational sociology.
 
−
 
 
−
在社会科学中，研究宏观属性的出现是从微观属性出发的，在社会学中又称为宏观-微观视角。这个话题通常被认为是社会的复杂性，常常与计算机模拟在社会科学中的应用有关。计算社会学。
 
−
 
 
−
 
 
−
 
 
−
Weaver perceived and addressed this problem, in at least a preliminary way, in drawing a distinction between "disorganized complexity" and "organized complexity".
 
−
 
 
−
 
 
−
 
 
−
In Weaver's view, disorganized complexity results from the particular system having a very large number of parts, say millions of parts, or many more. Though the interactions of the parts in a "disorganized complexity" situation can be seen as largely random, the properties of the system as a whole can be understood by using probability and statistical methods.
 
−
 
 
−
Systems theory has long been concerned with the study of complex systems (in recent times, complexity theory and complex systems have also been used as names of the field). These systems are present in the research of a variety disciplines, including biology, economics, social studies and technology. Recently, complexity has become a natural domain of interest of real world socio-cognitive systems and emerging systemics research. Complex systems tend to be high-dimensional, non-linear, and difficult to model. In specific circumstances, they may exhibit low-dimensional behaviour.
 
−
 
 
−
系统理论长期以来一直关注复杂系统的研究(近年来，复杂性理论和复杂系统也被用作该领域的名称)。这些系统存在于各种学科的研究中，包括生物学、经济学、社会研究和技术。近年来，复杂性已经成为现实世界社会认知系统和新兴系统学研究的一个自然领域。复杂系统往往是高维的、非线性的、难以建模的。在特定情况下，他们可能表现出低维度的行为。
 
−
 
 
−
 
 
−
 
 
−
A prime example of disorganized complexity is a gas in a container, with the gas molecules as the parts. Some would suggest that a system of disorganized complexity may be compared with the (relative) [[simplicity]] of planetary orbits – the latter can be predicted by applying [[Newton's laws of motion]]. Of course, most real-world systems, including planetary orbits, eventually become theoretically unpredictable even using Newtonian dynamics; as discovered by modern [[chaos theory]].<ref>"Sir James Lighthill and Modern Fluid Mechanics", by Lokenath Debnath, The University of Texas-Pan American, US, Imperial College Press: {{ISBN|978-1-84816-113-9}}: {{ISBN|1-84816-113-1}}, Singapore, page 31. Online at http://cs5594.userapi.com/u11728334/docs/25eb2e1350a5/Lokenath_Debnath_Sir_James_Lighthill_and_mode.pdf{{dead link|date=August 2017 |bot=InternetArchiveBot |fix-attempted=yes }}</ref>
 
−
 
 
−
 
 
−
 
 
−
In information theory, algorithmic information theory is concerned with the complexity of strings of data.
 
−
 
 
−
在信息论中，算法信息论关注的是数据串的复杂性。
 
−
 
 
−
Organized complexity, in Weaver's view, resides in nothing else than the non-random, or correlated, interaction between the parts. These correlated relationships create a differentiated structure that can, as a system, interact with other systems. The coordinated system manifests properties not carried or dictated by individual parts. The organized aspect of this form of complexity vis-a-vis to other systems than the subject system can be said to "emerge," without any "guiding hand".
 
−
 
 
−
 
 
−
 
 
−
Complex strings are harder to compress. While intuition tells us that this may depend on the codec used to compress a string (a codec could be theoretically created in any arbitrary language, including one in which the very small command "X" could cause the computer to output a very complicated string like "18995316"), any two Turing-complete languages can be implemented in each other, meaning that the length of two encodings in different languages will vary by at most the length of the "translation" language – which will end up being negligible for sufficiently large data strings.
 
−
 
 
−
复杂的字符串更难压缩。直觉告诉我们，这可能取决于用于压缩字符串的编解码器(编解码器理论上可以在任何语言中创建，包括一个非常小的命令“ x”可以导致计算机输出非常复杂的字符串，比如“18995316”) ，但是任何两种图灵完整语言都可以在彼此中实现，这意味着不同语言中两种编码器的长度最多只会随着“翻译”语言的长度而变化——这对于足够大数据字符串来说可以忽略不计。
 
−
 
 
−
The number of parts does not have to be very large for a particular system to have emergent properties. A system of organized complexity may be understood in its properties (behavior among the properties) through [[model (abstract)|modeling]] and [[simulation]], particularly [[computer simulation|modeling and simulation with computers]]. An example of organized complexity is a city neighborhood as a living mechanism, with the neighborhood people among the system's parts.
 
−
 
 
−
These algorithmic measures of complexity tend to assign high values to random noise. However, those studying complex systems would not consider randomness as complexity.
 
−
 
 
−
这些复杂度的算法测量倾向于给随机噪声赋予较高的值。然而，那些研究复杂系统的人并不认为随机性就是复杂性。
 
−
 
 
−
Information entropy is also sometimes used in information theory as indicative of complexity, but entropy is also high for randomness. Information fluctuation complexity, fluctuations of information about entropy, does not consider randomness to be complex and has been useful in many applications.
 
−
 
 
−
信息论中有时也会用熵表示复杂性，但是熵的随机性也很高。信息波动的复杂性，熵信息的波动性，不考虑随机性的复杂性，已经在许多应用中得到应用。
 
−
 
 
−
 
 
−
Recent work in machine learning has examined the complexity of the data as it affects the performance of supervised classification algorithms. Ho and Basu present a set of complexity measures for binary classification problems.
 
−
 
 
−
最近机器学习的工作已经检查了数据的复杂性，因为它影响了监督分类算法的性能。Ho 和 Basu 为二分类问题提出了一套复杂度量方法。
 
−
 
 
−
The complexity measures broadly cover:
 
−
 
 
−
复杂性指标大致涵盖:
 
−
 
 
−
 
 
−
 
 
−
== Sources and factors ==
 
−
 
 
−
Instance hardness is a bottom-up approach that first seeks to identify instances that are likely to be misclassified (or, in other words, which instances are the most complex). The characteristics of the instances that are likely to be misclassified are then measured based on the output from a set of hardness measures. The hardness measures are based on several supervised learning techniques such as measuring the number of disagreeing neighbors or the likelihood of the assigned class label given the input features. The information provided by the complexity measures has been examined for use in meta learning to determine for which data sets filtering (or removing suspected noisy instances from the training set) is the most beneficial and could be expanded to other areas.
 
−
 
 
−
实例硬度是一种自下而上的方法，它首先寻求识别可能被错误分类的实例(或者，换句话说，哪些实例是最复杂的)。然后，可能被错误分类的实例的特征根据一组硬度测量值的输出进行测量。硬度测量是基于一些监督式学习技术，如测量不同意的邻居的数量或分配的类标签的可能性给予输入特征。复杂性度量提供的信息已经被用于元学习，以确定哪些数据集过滤(或者从训练集中去除可疑的噪音实例)是最有益的，并且可以扩展到其他领域。
 
−
 
 
−
There are generally rules which can be invoked to explain the origin of complexity in a given system.
 
−
 
 
−
 
 
−
 
 
−
The source of disorganized complexity is the large number of parts in the system of interest, and the lack of correlation between elements in the system.
 
−
 
 
−
A recent study based on molecular simulations and compliance constants describes molecular recognition as a phenomenon of organisation.
 
−
 
 
−
最近一项基于分子模拟和顺应常数的研究将分子识别描述为一种组织现象。
 
−
 
 
−
 
 
−
 
 
−
Even for small molecules like carbohydrates, the recognition process can not be predicted or designed even assuming that each individual hydrogen bond's strength is exactly known.
 
−
 
 
−
即使是像碳水化合物这样的小分子，识别过程也不能被预测或设计，即使假设每个单独的氢键的强度是确切知道的。
 
−
 
 
−
In the case of self-organizing living systems, usefully organized complexity comes from beneficially mutated organisms being selected to survive by their environment for their differential reproductive ability or at least success over inanimate matter or less organized complex organisms. See e.g. [[Robert Ulanowicz]]'s treatment of ecosystems.<ref>Ulanowicz, Robert, "Ecology, the Ascendant Perspective", Columbia, 1997</ref>
 
−
 
 
−
 
 
−
 
 
−
Complexity of an object or system is a relative property. For instance, for many functions (problems), such a computational complexity as time of computation is smaller when multitape [[Turing machine]]s are used than when Turing machines with one tape are used. [[Random Access Machine]]s allow one to even more decrease time complexity (Greenlaw and Hoover 1998: 226), while inductive Turing machines can decrease even the complexity class of a function, language or set (Burgin 2005). This shows that tools of activity can be an important factor of complexity.
 
−
 
 
−
Computational complexity theory is the study of the complexity of problems – that is, the difficulty of solving them. Problems can be classified by complexity class according to the time it takes for an algorithm – usually a computer program – to solve them as a function of the problem size. Some problems are difficult to solve, while others are easy. For example, some difficult problems need algorithms that take an exponential amount of time in terms of the size of the problem to solve. Take the travelling salesman problem, for example. It can be solved in time <math>O(n^2 2^n)</math> (where n is the size of the network to visit – the number of cities the travelling salesman must visit exactly once). As the size of the network of cities grows, the time needed to find the route grows (more than) exponentially.
 
−
 
 
−
计算复杂性理论是研究问题的复杂性，也就是解决问题的难度。问题可以根据算法(通常是计算机程序)解决它们所需的时间(作为问题大小的函数)按复杂性类别进行分类。有些问题很难解决，而有些则很容易。例如，一些困难的问题需要算法花费指数量的时间来解决问题的大小。以旅行推销员问题为例。这个问题可以在时间上得到解决(其中 n 是要访问的网络的大小，也就是货郎担必须访问一次的城市数)。随着城市网络规模的扩大，寻找路线所需的时间呈指数增长(超过倍)。
 
−
 
 
−
 
 
−
 
 
−
== Varied meanings ==
 
−
 
 
−
Even though a problem may be computationally solvable in principle, in actual practice it may not be that simple. These problems might require large amounts of time or an inordinate amount of space. Computational complexity may be approached from many different aspects. Computational complexity can be investigated on the basis of time, memory or other resources used to solve the problem. Time and space are two of the most important and popular considerations when problems of complexity are analyzed.
 
−
 
 
−
即使一个问题在原则上是可以计算解决的，但在实际操作中可能没有那么简单。这些问题可能需要大量的时间或过多的空间。计算复杂性可以从许多不同的方面来看待。计算复杂性可以根据时间，内存或其他资源用于解决问题的基础上进行研究。在分析复杂性问题时，时间和空间是最重要和最普遍的两个考虑因素。
 
−
 
 
−
In several scientific fields, "complexity" has a precise meaning:
 
−
 
 
−
 
 
−
 
 
−
There exist a certain class of problems that although they are solvable in principle they require so much time or space that it is not practical to attempt to solve them. These problems are called intractable.
 
−
 
 
−
有一类问题，虽然原则上是可以解决的，但是它们需要很多时间和空间，因此试图解决它们是不切实际的。这些问题被称为棘手的。
 
−
 
 
−
* In [[computational complexity theory]], the [[Computational resource|amounts of resources]] required for the execution of [[algorithm]]s is studied. The most popular types of computational complexity are the time complexity of a problem equal to the number of steps that it takes to solve an instance of the problem as a function of the [[problem size|size of the input]] (usually measured in bits), using the most efficient algorithm, and the space complexity of a problem equal to the volume of the [[computer storage|memory]] used by the algorithm (e.g., cells of the tape) that it takes to solve an instance of the problem as a function of the size of the input (usually measured in bits), using the most efficient algorithm. This allows classification of computational problems by [[complexity class]] (such as [[P (complexity)|P]], [[NP (complexity)|NP]], etc.). An axiomatic approach to computational complexity was developed by [[Manuel Blum]]. It allows one to deduce many properties of concrete computational complexity measures, such as time complexity or space complexity, from properties of axiomatically defined measures.
 
−
 
 
−
* In [[algorithmic information theory]], the ''[[Kolmogorov complexity]]'' (also called ''descriptive complexity'', ''algorithmic complexity'' or ''algorithmic entropy'') of a [[string (computer science)|string]] is the length of the shortest binary [[computer program|program]] that outputs that string. [[Minimum message length]] is a practical application of this approach. Different kinds of Kolmogorov complexity are studied: the uniform complexity, prefix complexity, monotone complexity, time-bounded Kolmogorov complexity, and space-bounded Kolmogorov complexity. An axiomatic approach to Kolmogorov complexity based on [[Blum axioms]] (Blum 1967) was introduced by Mark Burgin in the paper presented for publication by [[Andrey Kolmogorov]].<ref>Burgin, M. (1982) Generalized Kolmogorov complexity and duality in theory of computations, Notices of the Russian Academy of Sciences, v.25, No. 3, pp. 19–23</ref> The axiomatic approach encompasses other approaches to Kolmogorov complexity. It is possible to treat different kinds of Kolmogorov complexity as particular cases of axiomatically defined generalized Kolmogorov complexity. Instead of proving similar theorems, such as the basic invariance theorem, for each particular measure, it is possible to easily deduce all such results from one corresponding theorem proved in the axiomatic setting. This is a general advantage of the axiomatic approach in mathematics. The axiomatic approach to Kolmogorov complexity was further developed in the book (Burgin 2005) and applied to software metrics (Burgin and Debnath, 2003; Debnath and Burgin, 2003).
 
−
 
 
−
There is another form of complexity called hierarchical complexity. It is orthogonal to the forms of complexity discussed so far, which are called horizontal complexity.
 
−
 
 
−
还有另外一种复杂性，叫做层次复杂性。它与迄今为止所讨论的复杂性的形式是正交的，即所谓的横向复杂性。
 
−
 
 
−
*In [[information theory]], [[information fluctuation complexity]] is the fluctuation of information about [[Entropy (information theory)|information entropy]]. It is derivable from fluctuations in the predominance of order and chaos in a dynamic system and has been used as a measure of complexity in many diverse fields.
 
−
 
 
−
* In [[information processing]], complexity is a measure of the total number of [[property|properties]] transmitted by an object and detected by an [[observation|observer]]. Such a collection of properties is often referred to as a [[state (computer science)|state]].
 
−
 
 
−
* In [[physical systems]], complexity is a measure of the [[probability]] of the [[Quantum state|state vector]] of the system. This should not be confused with [[entropy (statistical thermodynamics)|entropy]]; it is a distinct mathematical measure, one in which two distinct states are never conflated and considered equal, as is done for the notion of entropy in [[statistical mechanics]].
 
−
 
 
−
* In [[dynamical systems]], statistical complexity measures the size of the minimum program able to statistically reproduce the patterns (configurations) contained in the data set (sequence).<ref>{{Cite journal |last1=Crutchfield |first1=J.P. |last2=Young |first2=K. |year=1989 |title=Inferring statistical complexity |journal=[[Physical Review Letters]] |volume=63 |issue=2 |pages=105–108|doi=10.1103/PhysRevLett.63.105 |pmid=10040781 |bibcode=1989PhRvL..63..105C }}</ref><ref>{{Cite journal |last1=Crutchfield |first1=J.P. |last2=Shalizi |first2=C.R. |year=1999
 
−
 
 
−
|title=Thermodynamic depth of causal states: Objective complexity via minimal representations |journal=[[Physical Review E]] |volume=59 |issue=1 |pages=275–283
 
−
 
 
−
|doi=10.1103/PhysRevE.59.275 |bibcode=1999PhRvE..59..275C }}</ref> While the algorithmic complexity implies a deterministic description of an object (it measures the information content of an individual sequence), the statistical complexity, like [[forecasting complexity]],<ref>{{cite journal |last1=Grassberger |first1=P. |year=1986 |title=Toward a quantitative theory of self-generated complexity |journal=[[International Journal of Theoretical Physics]] |volume=25 |issue=9 |pages=907–938 |doi=10.1007/bf00668821|bibcode=1986IJTP...25..907G|s2cid=16952432 }}</ref> implies a statistical description, and refers to an ensemble of sequences generated by a certain source. Formally, the statistical complexity reconstructs a minimal model comprising the collection of all histories sharing a similar probabilistic future, and measures the [[entropy (information theory)|entropy]] of the probability distribution of the states within this model. It is a computable and observer-independent measure based only on the internal dynamics of the system, and has been used in studies of [[emergence]] and [[self-organization]].<ref>{{cite journal
 
−
 
 
−
  |last1=Prokopenko |first1=M. |last2=Boschetti |first2=F. |last3=Ryan |first3=A. |year=2009 |title=An information-theoretic primer on complexity, self-organisation and emergence |journal=Complexity |volume=15 |issue=1 |pages=11–28 |doi=10.1002/cplx.20249 |bibcode=2009Cmplx..15a..11P }}</ref>
 
−
 
 
−
* In [[mathematics]], [[Krohn–Rhodes complexity]] is an important topic in the study of finite [[semigroup]]s and [[automata theory|automata]].
 
−
 
 
−
* In [[Network theory]] complexity is the product of richness in the connections between components of a system,<ref>A complex network analysis example: "[http://www.martingrandjean.ch/complex-structures-and-international-organizations/ Complex Structures and International Organizations]" ({{Cite journal | volume = | issue = 2| last = Grandjean| first = Martin| title = Analisi e visualizzazioni delle reti in storia. L'esempio della cooperazione intellettuale della Società delle Nazioni | journal = Memoria e Ricerca | date = 2017| pages = 371–393| doi = 10.14647/87204}} See also: [https://halshs.archives-ouvertes.fr/halshs-01610098v2 French version]).</ref> and defined by a very unequal distribution of certain measures (some elements being highly connected and some very few, see [[complex network]]).
 
−
 
 
−
* In [[software engineering]], [[programming complexity]] is a measure of the interactions of the various elements of the software. This differs from the computational complexity described above in that it is a measure of the design of the software.
 
−
 
 
−
* In [[Abstract and concrete|abstract]] sense – Abstract Complexity, is based on visual structures [[perception]] <ref>Mariusz Stanowski (2011) Abstract Complexity Definition, Complicity 2, p.78-83 [https://ejournals.library.ualberta.ca/index.php/complicity/article/view/11156]</ref> It is complexity of binary string defined as a square of features number divided by number of elements (0's and 1's). Features comprise here all distinctive arrangements of 0's and 1's. Though the features number have to be always approximated the definition is precise and meet intuitive criterion.
 
−
 
 
−
 
 
−
 
 
−
Other fields introduce less precisely defined notions of complexity:
 
−
 
 
−
 
 
−
 
 
−
* A [[complex adaptive system]] has some or all of the following attributes:<ref name="Neil Johnson" />
 
−
 
 
−
** The number of parts (and types of parts) in the system and the number of relations between the parts is non-trivial – however, there is no general rule to separate "trivial" from "non-trivial";
 
−
 
 
−
** The system has memory or includes [[feedback]];
 
−
 
 
−
** The system can adapt itself according to its history or feedback;
 
−
 
 
−
** The relations between the system and its environment are non-trivial or non-linear;
 
−
 
 
−
** The system can be influenced by, or can adapt itself to, its environment;
 
−
 
 
−
** The system is highly sensitive to initial conditions.
 
−
 
 
−
 
 
−
 
 
−
== Study ==
 
−
 
 
−
Complexity has always been a part of our environment, and therefore many scientific fields have dealt with complex systems and phenomena. From one perspective, that which is somehow complex – displaying variation without being [[randomness|random]] – is most worthy of interest given the rewards found in the depths of exploration.
 
−
 
 
−
 
 
−
 
 
−
The use of the term complex is often confused with the term complicated. In today's systems, this is the difference between myriad connecting "stovepipes" and effective "integrated" solutions.<ref>[[Lissack, Michael R.]]; [[Johan Roos]] (2000). ''The Next Common Sense, The e-Manager's Guide to Mastering Complexity.'' Intercultural Press. {{ISBN|978-1-85788-235-3}}.
 
−
 
 
−
</ref> This means that complex is the opposite of independent, while complicated is the opposite of simple.
 
−
 
 
−
 
 
−
 
 
−
While this has led some fields to come up with specific definitions of complexity, there is a more recent movement to regroup observations [[interdisciplinarity|from different fields]] to study complexity in itself, whether it appears in [[anthill]]s, [[human brain]]s, or [[stock market]]s, social systems.<ref>{{Cite journal|url=https://www.academia.edu/30193748|title=Complexics as a meta-transdisciplinary field|last=Bastardas-Boada|first=Albert|date=|journal=Congrès Mondial Pour la Pensée Complexe. Les Défis d'Un Monde Globalisé. (Paris, 8-9 Décembre). Unesco|access-date=}}</ref> One such interdisciplinary group of fields is [[relational order theories]].
 
−
 
 
−
 
 
−
 
 
−
== Topics ==
 
−
 
 
−
=== Behaviour ===
 
−
 
 
−
The behavior of a complex system is often said to be due to emergence and [[self-organization]]. Chaos theory has investigated the sensitivity of systems to variations in initial conditions as one cause of complex behaviour.
 
−
 
 
−
 
 
−
 
 
−
===Mechanisms ===
 
−
 
 
−
Recent developments around [[artificial life]], [[evolutionary computation]] and [[genetic algorithm]]s have led to an increasing emphasis on complexity and [[complex adaptive systems]].
 
−
 
 
−
 
 
−
=== Simulations ===
 
−
 
 
−
 
 
−
In [[social science]], the study on the emergence of macro-properties from the micro-properties, also known as macro-micro view in [[sociology]]. The topic is commonly recognized as [[social complexity]] that is often related to the use of computer simulation in social science, i.e.: [[computational sociology]].
 
−
 
 
−
 
 
−
生物科学理论
 
−
 
 
−
 
 
−
 
 
−
=== Systems ===
 
−
 
 
−
 
 
−
[[Systems theory]] has long been concerned with the study of [[complex system]]s (in recent times, ''complexity theory'' and ''complex systems'' have also been used as names of the field). These systems are present in the research of a variety disciplines, including [[biology]], [[economics]], social studies and [[technology]]. Recently, complexity has become a natural domain of interest of real world socio-cognitive systems and emerging [[systemics]] research. Complex systems tend to be high-[[dimension]]al, [[non-linearity|non-linear]], and difficult to model. In specific circumstances, they may exhibit low-dimensional behaviour.
 
−
 
 
−
 
 
−
=== Data ===
 
−
 
 
−
In [[information theory]], algorithmic information theory is concerned with the complexity of strings of data.
 
−
 
 
−
Complex strings are harder to compress. While intuition tells us that this may depend on the [[codec]] used to compress a string (a codec could be theoretically created in any arbitrary language, including one in which the very small command "X" could cause the computer to output a very complicated string like "18995316"), any two [[Turing completeness|Turing-complete]] languages can be implemented in each other, meaning that the length of two encodings in different languages will vary by at most the length of the "translation" language – which will end up being negligible for sufficiently large data strings.
 
−
 
 
−
These algorithmic measures of complexity tend to assign high values to [[signal noise|random noise]]. However, those studying complex systems would not consider randomness as complexity{{who|date=October 2013}}.
 
−
 
 
−
 
 
−
[[Information entropy]] is also sometimes used in information theory as indicative of complexity, but entropy is also high for randomness. [[Information fluctuation complexity]], fluctuations of information about entropy, does not consider randomness to be complex and has been useful in many applications.
 
−
 
 
−
 
 
−
Recent work in [[machine learning]] has examined the complexity of the data as it affects the performance of [[Supervised learning|supervised]] classification algorithms. Ho and Basu present a set of [[Computational complexity theory|complexity measures]] for [[binary classification]] problems.<ref>Ho, T.K.; Basu, M. (2002). "[http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=990132&tag=1 Complexity Measures of Supervised Classification Problems]". IEEE Transactions on Pattern Analysis and Machine Intelligence 24 (3), pp 289–300.</ref>
 
−
 
 
−
 
 
−
The complexity measures broadly cover:
 
−
 
 
−
* the overlaps in feature values from differing classes.
 
−
 
 
−
* the separability of the classes.
 
−
 
 
−
* measures of geometry, topology, and density of [[manifold]]s. Instance hardness is another approach seeks to characterize the data complexity with the goal of determining how hard a data set is to classify correctly and is not limited to binary problems.<ref>Smith, M.R.; Martinez, T.; Giraud-Carrier, C. (2014). "[https://link.springer.com/article/10.1007%2Fs10994-013-5422-z An Instance Level Analysis of Data Complexity]". Machine Learning, 95(2): 225–256.</ref>
 
−
 
 
−
Instance hardness is a bottom-up approach that first seeks to identify instances that are likely to be misclassified (or, in other words, which instances are the most complex). The characteristics of the instances that are likely to be misclassified are then measured based on the output from a set of hardness measures. The hardness measures are based on several supervised learning techniques such as measuring the number of disagreeing neighbors or the likelihood of the assigned class label given the input features. The information provided by the complexity measures has been examined for use in [[Meta learning (computer science)|meta learning]] to determine for which data sets filtering (or removing suspected noisy instances from the training set) is the most beneficial<ref>{{cite journal|title= Predicting Noise Filtering Efficacy with Data Complexity Measures for Nearest Neighbor Classification|journal= Pattern Recognition|volume= 46|pages= 355–364|doi= 10.1016/j.patcog.2012.07.009|year= 2013|last1= Sáez|first1= José A.|last2= Luengo|first2= Julián|last3= Herrera|first3= Francisco}}</ref> and could be expanded to other areas.
 
−
 
 
−
 
 
−
=== In molecular recognition ===
 
−
 
 
−
 
 
−
A recent study based on molecular simulations and compliance constants describes [[molecular recognition]] as a phenomenon of organisation.<ref>{{cite journal | title=Complexity in molecular recognition | author=Jorg Grunenberg | journal=Phys. Chem. Chem. Phys. | year=2011 | volume=13 | issue=21 | pages= 10136–10146 | doi=10.1039/c1cp20097f| pmid=21503359 | bibcode=2011PCCP...1310136G }}</ref>
 
−
 
 
−
 
 
−
Even for small molecules like [[carbohydrates]], the recognition process can not be predicted or designed even assuming that each individual [[hydrogen bond]]'s strength is exactly known.
 
−
 
 
−
 
 
−
== Applications ==
 
−
 
 
−
 
 
−
Computational complexity theory is the study of the complexity of problems – that is, the difficulty of [[problem solving|solving]] them. Problems can be classified by complexity class according to the time it takes for an algorithm – usually a computer program – to solve them as a function of the problem size. Some problems are difficult to solve, while others are easy. For example, some difficult problems need algorithms that take an exponential amount of time in terms of the size of the problem to solve. Take the [[travelling salesman problem]], for example. It can be solved in time <math>O(n^2 2^n)</math> (where ''n'' is the size of the network to visit – the number of cities the travelling salesman must visit exactly once). As the size of the network of cities grows, the time needed to find the route grows (more than) exponentially.
 
−
 
 
−
 
 
−
 
 
−
Even though a problem may be computationally solvable in principle, in actual practice it may not be that simple. These problems might require large amounts of time or an inordinate amount of space. [[Analysis of algorithms|Computational complexity]] may be approached from many different aspects. Computational complexity can be investigated on the basis of time, memory or other resources used to solve the problem. Time and space are two of the most important and popular considerations when problems of complexity are analyzed.
 
−
 
 
−
 
 
−
There exist a certain class of problems that although they are solvable in principle they require so much time or space that it is not practical to attempt to solve them. These problems are called [[Computational complexity theory#Intractability|intractable]].
 
−
 
 
−
 
 
−
 
 
−
There is another form of complexity called [[Model of hierarchical complexity|hierarchical complexity]]. It is orthogonal to the forms of complexity discussed so far, which are called horizontal complexity.
 
−
 
 
−
 
 
−
== References ==
 
−
 
 
−
{{reflist}}
 
−
 
 
−
 
 
−
 
 
−
== Further reading ==
 
−
 
 
−
{{refbegin}}
 
−
 
 
−
<noinclude>
 
−
 
 
−
<small>This page was moved from [[wikipedia:en:Complexity]]. Its edit history can be viewed at [[复杂性/edithistory]]</small></noinclude>
 
−
 
 
−
[[Category:待整理页面]]
 

2021年8月7日 (六) 13:36的版本

The complexity of a physical system or a dynamical process expresses the degree to which components engage in organized structured interactions. High complexity is achieved in systems that exhibit a mixture of order and disorder (randomness and regularity) and that have a high capacity to generate emergent phenomena.

物理系统或动态过程的复杂性表达了组件参与有组织的结构化交互的程度。高度复杂的系统实现了有序和无序(规律性和随机性)的混合，并有很高的可能产生涌现现象。


各学科中的复杂性

Despite the importance and ubiquity of the concept of complexity in modern science and society, no general and widely accepted means of measuring the complexity of a physical object, system, or process currently exists. The lack of any general measure may reflect the nascent stage of our understanding of complex systems, which still lacks a general unified framework that cuts across all natural and social sciences. While a general measure has remained elusive until now, there is a broad spectrum of measures of complexity that apply to specific types of systems or problem domains. The justification for each of these measures often rests on their ability to produce intuitively correct values at the extremes of the complexity spectrum. Despite the heterogeneous approaches taken to defining and measuring complexity, the belief persists that there are properties common to all complex systems, and new proposals are continually being produced and tested by an interdisciplinary community of physicists, biologists, mathematicians, computer scientists, economists and social theorists.

尽管复杂性的概念在现代科学和社会中非常重要和普遍存在，但目前还没有一种普遍的、广泛接受的方法来衡量一个物理对象、系统或过程的复杂性。缺乏普遍的衡量标准，可能反映了我们对复杂系统的理解处于初始阶段，缺乏一个贯穿所有自然科学和社会科学的普遍的统一框架。虽然到目前为止，一般性的衡量标准仍然难以捉摸，但是，我们拥有许多适用于具体类型的系统或问题领域的复杂性衡量标准。尽管在定义和测量复杂性方面存在了各种不同的方法，但有一种信念仍然坚持认为所有复杂系统都有共同的特性，而且新的定义和度量正在不断地被一个由物理学家、生物学家、数学家、计算机科学家、经济学家和社会理论家组成的跨学科团体提出和检验。


This article deals with complexity from an information-theoretical perspective. A treatment of complexity from the perspective of dynamical systems can be found in another article (Complex Systems).

本文从信息论的角度探讨复杂性问题。读者还可以从系统论的角度出发理解复杂性。


复杂性的一般特征

Quantitative or analytic definitions of complexity often disagree about the precise formulation, or indeed even the formal framework within which complexity is to be defined. Yet, there is an informal notion of complexity based upon some of the ingredients that are shared by most if not all complex systems and processes. Herbert Simon was among the first to discuss the nature and architecture of complex systems (Simon, 1981) and he suggested to define complex systems as those that are “made up of a large number of parts that have many interactions.” Simon goes on to note that “in such systems the whole is more than the sum of the parts in the […] sense that, given the properties of the parts and the laws of their interaction, it is not a trivial matter to infer the properties of the whole.”

复杂性的定量或分析学（analytic）定义往往不同意精确的表述，甚至不同意定义复杂性的正式框架。然而，有一种非正式的复杂性概念，它基于大多数(如果不是所有的话)复杂系统和过程所共有的一些要素。赫伯特 · 西蒙是最早讨论复杂系统的性质和结构的人之一(Simon，1981) ，他建议将复杂系统定义为那些“由大量具有许多相互作用的部分组成”的系统。西蒙接着指出，“在这样的系统中，整体不仅仅在[ ... ]的意义上大于各部分之和，考虑到各部分的性质及其相互作用的规律，推断整体的性质不是一件容易事。”


Components. Many complex systems can be decomposed into components (elements, units) that are structurally distinct, and may function as individuals, generating some form of local behavior, activity or dynamics. Components of complex systems may themselves be decomposable into subcomponents, resulting in systems that are complex at multiple levels of organization, forming hierarchies of nearly, but not completely decomposable components.

组分 许多复杂的系统可以分解成结构上不同的组成部分(组件、元素、单元) ，且它们可以作为个体发挥作用，产生某种形式的局部行为、活动或动态。复杂系统的组件本身可以分解为子组件，导致系统在多层次的组织中是复杂的，形成（不完全）可分解的组件层次结构。


Interactions. Components of complex systems engage in dynamic interactions, resulting in integration or binding of these components across space and time into an organized whole. Interactions often modulate the individual actions of the components, thus altering their local functionality by relaying global context. In many complex systems, interactions between subsets of components are mediated by some form of communication paths or connections. Such structured interactions are often sparse, i.e. only a small subset of all possible interactions is actually realized within the system. The specific patterns of these interactions are crucial in determining how the system functions as a whole. Some interactions between components may be strong, in the sense that they possess great efficacy with respect to individual components. Other interactions may be considered weak, as their effects are limited in size or sporadic across time. Both, strong and weak interactions can have significant effects on the system as a whole.

交互 复杂系统的组成部分进行动态交互，导致这些组成部分跨空间和时间整合成一个有组织的整体。交互通常能调节组件的单个动作，从而通过中继全局上下文 relaying global context 改变其局部功能。在许多复杂系统中，组件子集之间的交互是通过某种形式的通信路径或连接进行的。这样的结构化交互通常是稀疏的，也就是说，所有可能的交互中只有一小部分是在系统中实现的。这些相互作用的具体模式对于确定系统作为一个整体如何运作至关重要。组件之间的某些相互作用可能很强，因为它们对于单个组件具有很大的效力。其他相互作用可能被认为是弱的，因为他们的影响范围或时间是有限的。无论是强相互作用还是弱相互作用，都能对整个系统产生重大影响。


Emergence. Interactions between components in integrated systems often generate phenomena, functions, or effects that cannot be trivially reduced to properties of the components alone. Instead these functions emerge as a result of structured interactions and are properties of the system as a whole. In many cases, even a detailed and complete examination of the individual components will fail to predict the range of emergent processes that these components are capable of if allowed to interact as part of a system. In turn, dissection of an integrated system into components and interactions generally results in a loss of the emergent process.

In summary, systems with numerous components capable of structured interactions that generate emergent phenomena may be called complex. The observation of complex systems poses many challenges, as an observer needs simultaneously to record states and state transitions of many components and interactions. Such observations require that choices be made concerning the definition of states, state space and time resolution. How states are defined and measured can impact other derived measures such as those of system complexity.

Complexity as a mixture of order and disorder. Drawn after Huberman and Hogg (1986).

复杂性的度量

Measures of complexity allow different systems to be compared to each other by applying a common metric. This is especially meaningful for systems that are structurally or functionally related. Differences in complexity among such related systems may reveal features of their organization that promote complexity.

Some measures of complexity are algorithmic in nature and attempt to identify a minimal description length. For these measures complexity applies to a description, not the system or process per se. Other measures of complexity take into account the time evolution of a system and often build on the theoretical foundations of statistical information theory.

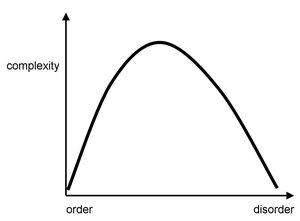
Most extant complexity measures can be grouped into two main categories. Members of the first category (algorithmic information content and logical depth) all capture the randomness, information content or description length of a system or process, with random processes possessing the highest complexity since they most resist compression. The second category (including statistical complexity, physical complexity and neural complexity) conceptualizes complexity as distinct from randomness. Here, complex systems are those that possess a high amount of structure or information, often across multiple temporal and spatial scales. Within this category of measures, highly complex systems are positioned somewhere between systems that are highly ordered (regular) or highly disordered (random). <figref>Complexity_figure1.jpg</figref> shows a schematic diagram of the shape of such measures, however, it should be emphasized again that a generally accepted quantitative expression linking complexity and disorder does not currently exist.

复杂与随机

Algorithmic information content was defined (Kolmogorov, 1965; Chaitin, 1977) as the amount of information contained in a string of symbols given by the length of the shortest computer program that generates the string. Highly regular, periodic or monotonic strings may be computed by programs that are short and thus contain little information, while random strings require a program that is as long as the string itself, thus resulting in high (maximal) information content. Algorithmic information content (AIC) captures the amount of randomness of symbol strings, but seems ill suited for applications to biological or neural systems and, in addition, has the inconvenient property of being uncomputable. For further discussion see algorithmic information theory.

Logical Depth (Bennett, 1988) is related to AIC and draws additionally on computational complexity defined as the minimal amount of computational resources (time, memory) needed to solve a given class of problem. Complexity as logical depth refers mainly to the running time of the shortest program capable of generating a given string or pattern. Similarly to AIC, complexity as logical depth is a measure of a generative process and does not apply directly to an actually existing physical system or dynamical process. Computing logical depth requires knowing the shortest computer program, thus the measure is subject to the same fundamental limitation as AIC.

Effective measure complexity (Grassberger, 1986) quantifies the complexity of a sequence by the amount of information contained in a given part of the sequence that is needed to predict the next symbol. Effective measure complexity can capture structure in sequences that range over multiple scales and it is related to the extensivity of entropy (see below).

Thermodynamic depth (Lloyd and Pagels, 1988) relates the entropy of a system to the number of possible historical paths that led to its observed state, with “deep” systems being all those that are “hard to build”, whose final state carries much information about the history leading up to it. The emphasis on how a system comes to be, its generative history, identifies thermodynamic depth as a complementary measure to logical depth. While thermodynamic depth has the advantage of being empirically calculable, problems with the definition of system states have been noted (Crutchfield and Shalizi, 1999). Although aimed at distinguishing complex systems as different from random ones, its formalism essentially captures the amount of randomness created by a generative process, and does not differentiate regular from random systems.

作为结构和信息的复杂性

A simple way of quantifying complexity on a structural basis would be to count the number of components and/or interactions within a system. An examination of the number of structural parts (McShea, 1996) and functional behaviors of organisms across evolution demonstrates that these measures increase over time, a finding that contributes to the ongoing debate over whether complexity grows as a result of natural selection. However, numerosity alone may only be an indicator of complicatedness, but not necessarily of complexity. Large and highly coupled systems may not be more complex than those that are smaller and less coupled. For example, a very large system that is fully connected can be described in a compact manner and may tend to generate uniform behavior, while the description of a smaller but more heterogeneous system may be less compressible and its behavior may be more differentiated.

Effective complexity (Gell-Mann, 1995) measures the minimal description length of a system’s regularities. As such, this measure is related to AIC, but it attempts to distinguish regular features from random or incidental ones and therefore belongs within the family of complexity measures that aim at capturing how much structure a system contains. The separation of regular features from random ones may be difficult for any given empirical system, and it may crucially depend on criteria supplied by an external observer.

Physical complexity (Adami and Cerf, 2000) is related to effective complexity and is designed to estimate the complexity of any sequence of symbols that is about a physical world or environment. As such the measure is particularly useful when applied to biological systems. It is defined as the Kolmogorov complexity (AIC) that is shared between a sequence of symbols (such as a genome) and some description of the environment in which that sequence has meaning (such as an ecological niche). Since the Kolmogorov complexity is not computable, neither is the physical complexity. However, the average physical complexity of an ensemble of sequences (e.g. the set of genomes of an entire population of organisms) can be approximated by the mutual information between the ensembles of sequences (genomes) and their environment (ecology). Experiments conducted in a digital ecology (Adami, 2002) demonstrated that the mutual information between self-replicating genomes and their environment increased along evolutionary time. Physical complexity has also been used to estimate the complexity of biomolecules. The structural and functional complexity of a set of RNA molecules were shown to positively correlate with physical complexity (Carothers et al., 2004), indicating a possible link between functional capacities of evolved molecular structures and the amount of information they encode.

Statistical complexity (Crutchfield and Young, 1989) is a component of a broader theoretic framework known as computational mechanics, and can be calculated directly from empirical data. To calculate the statistical complexity, each point in the time series is mapped to a corresponding symbol according to some partitioning scheme, so that the raw data is now a stream of consecutive symbols. The symbol sequences are then clustered into causal states according to the following rule: two symbol sequences (i.e. histories of the dynamics) are contained in the same causal state if the conditional probability of any future symbol is identical for these two histories. In other words, two symbol sequences are considered to be the same if, on average, they predict the same distribution of future dynamics. Once these causal states have been identified, the transition probabilities between causal states can be extracted from the data, and the long-run probability distribution over all causal states can be calculated. The statistical complexity is then defined as the Shannon entropy of this distribution over causal states. Statistical complexity can be calculated analytically for abstract systems such as the logistic map, cellular automata and many basic Markov processes, and computational methods for constructing appropriate causal states in real systems, while taxing, exist and have been applied in a variety of contexts.

Predictive information (Bialek et al., 2001), while not in itself a complexity measure, can be used to separate systems into different complexity categories based on the principle of the extensivity of entropy. Extensivity manifests itself, for example, in systems composed of increasing numbers of homogeneous independent random variables. The Shannon entropy of such systems will grow linearly with their size. This linear growth of entropy with system size is known as extensivity. However, the constituent elements of a complex system are typically inhomogeneous and interdependent, so that as the number of random variables grows the entropy does not always grow linearly. The manner in which a given system departs from extensivity can be used to characterize its complexity.

Movie frames from a demonstration model of neural dynamics, consisting of 1600 spontaneously active Wison-Cowan neural mass units arranged on a sphere and coupled by excitatory connections. Three cases are shown: sparse coupling (local connections only), uniform coupling (global connections only), and a mixture of local and global connections (forming a small-world network). Neural complexity (Tononi et al., 1994; Sporns et al., 2000) is high only for the last case.

Neural complexity (Tononi et al., 1994), which may be applied to any empirically observed system including brains, is related to the extensivity of a system. One of its building blocks is integration (also called multi-information), a multivariate extension of mutual information that estimates the total amount of statistical structure within an arbitrarily large system. Integration is computed as the difference between the sum of the component’s individual entropies and the joint entropy of the system as a whole. The distribution of integration across multiple spatial scales captures the complexity of the system. Consider the following three cases (<figref>Complexity_figure2.jpg</figref>). (1) A system with components that are statistically independent will exhibit globally disordered or random dynamics. Its joint entropy will be exactly equal to the sum of the component entropies, and system integration will be zero, regardless of which spatial scale of the system is examined. (2) Any statistical dependence between components will lead to a contraction of the system’s joint entropy relative to the individual entropies, resulting in positive integration. If the components of a system are highly coupled and exhibit statistical dependencies as well as homogeneous dynamics (i.e. all components behave identically) then estimates of integration across multiple spatial scales of the system will, on average, follow a linear distribution. (3) If statistical dependencies are inhomogeneous (for example involving groupings of components, modules, or hierarchical patterns) the distribution of integration will deviate from linearity. The total amount of deviation is the system’s complexity. The complexity of a random system is zero, while the complexity of a homogeneous coupled (regular) system is very low. Systems with rich structure and dynamic behavior have high complexity.

Applied to neural dynamics, complexity as defined by Tononi et al. (1994) was found to be associated with specific patterns of neural connectivity, for example those exhibiting attributes of small-world networks (Sporns et al., 2000). Descendants of this complexity measure have addressed the matching of systems to an environment as well as their degeneracy, i.e. their capacity to produce functionally equivalent behaviors in different ways.

复杂网络

Traditionally, complex systems have been analyzed using tools from nonlinear dynamics and statistical information theory. Recently, the analytical framework of complex networks has led to a significant reappraisal of commonalities and differences between complex systems found in different scientific domains (Amaral and Ottino, 2004). A key insight is that network topology, the graph structure of the interactions, places important constraints on the system's dynamics, by directing information flow, creating patterns of coherence between components, and by shaping the emergence of macroscopic system states. Complexity is highly sensitive to changes in network topology (Sporns et al., 2000). Changes in connection patterns or strengths may thus serve as modulators of complexity. The link between network structure and dynamics represents one of the most promising areas of complexity research in the near future.

为什么是复杂性？

Why does complexity exist in the first place, especially among biological systems? A definitive answer to this question remains elusive. One perspective is based on the evolutionary demands biological systems face. The evolutionary success of biological structures and organisms depends on their ability to capture information about the environment, be it molecular or ecological. Biological complexity may then emerge as a result of evolutionary pressure on the effective encoding of structured relationships which support differential survival.

Another clue may be found in the emerging link between complexity and network structure. Complexity appears very prominently in systems that combine segregated and heterogeneous components with large-scale integration. Such systems become more complex as they more efficiently integrate more information, that is, as they become more capable to accommodate both the existence of specialized components that generate information and the existence of structured interactions that bind these components into a coherent whole. Thus reconciling parts and wholes, complexity may be a necessary manifestation of a fundamental dialectic in nature.

引用

  • Adami, C. (2002) What is complexity? BioEssays 24, 1085-1094.
  • Adami, C., Cerf, N.J. (2000) Physical complexity of symbolic sequences. Physica D 137, 62-69.
  • Amaral, L.A.N., Ottino, J.M. (2004) Complex networks. Eur. Phys. J. B 38, 147-162.
  • Bennett, C.H. (1988) Logical depth and physical complexity. In: R. Herken (ed.): The Universal Turing Machine. A Half-Century Survey. Pp. 227-257, Oxford: Oxford University Press.
  • Bialek, W., Nemenman, I., Tishby, N. (2001) Predictability, complexity, and learning. Neural Computation 13, 2409-2463.
  • Carothers, J.M., Oestreich, S.C., Davis, J.H., and Szostak, J.W. (2004) Informational complexity and functional activity of RNA structures. J. Am. Chem. Soc. 126, 5130–5137.
  • Chaitin, G.J. (1977) Algorithmic information theory. IBM Journal of Research and Development 21, 350-359. [1]
  • Crutchfield, J.P., Young, K. (1989) Inferring statistical complexity. Phys. Rev. Lett. 63, 105-109.
  • Crutchfield, J.P., Shalizi, C.R. (1999) Thermodynamic depth of causal states: Objective complexity via minimal representations. Phys. Rev. E 59, 275-283.
  • Gell-Mann, M. (1995) What is complexity? Complexity 1, 16-19.
  • Grassberger, P. (1986) Toward a quantitative theory of self-generated complexity. Int. J. Theor. Phys. 25, 907-928.
  • Huberman, B.A., Hogg, T. (1986) Complexity and adaptation. Physica D 22, 376-384.
  • Kolmogorov, A. N. (1965) Three approaches to the quantitative definition of information. Problems of Information Transmission 1, 1-17.
  • Lloyd, S., Pagels, H. (1988) Complexity as thermodynamic depth. Annals of Physics 188, 186-213.
  • McShea, D.W. (1995) Metazoan complexity and evolution: Is there a trend? Evolution 50, 477-492.
  • Simon, H.A. (1981) The Sciences of the Artificial. MIT Press: Cambridge.
  • Sporns, O., Tononi, G., Edelman, G.M. (2000) Theoretical neuroanatomy: Relating anatomical and functional connectivity in graphs and cortical connection matrices. Cereb. Cortex 10, 127-141.
  • Tononi, G., Sporns, O., Edelman, G.M. (1994) A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. U.S.A. 91, 5033-5037.


Scholarpedia内部引用

  • Marcus Hutter (2007) Algorithmic information theory. Scholarpedia, 2(3):2519.
  • Valentino Braitenberg (2007) Brain. Scholarpedia, 2(11):2918.
  • Gregoire Nicolis and Catherine Rouvas-Nicolis (2007) Complex systems. Scholarpedia, 2(11):1473.
  • James Meiss (2007) Dynamical systems. Scholarpedia, 2(2):1629.
  • Tomasz Downarowicz (2007) Entropy. Scholarpedia, 2(11):3901.
  • Arkady Pikovsky and Michael Rosenblum (2007) Synchronization. Scholarpedia, 2(12):1459.

外部链接

取自“https://wiki.swarma.org/index.php?title=复杂性&oldid=25571”