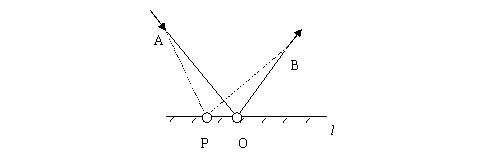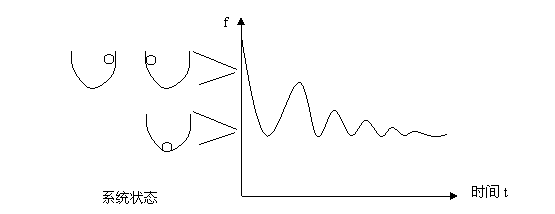生命之流(3)——过去与未来在现在相遇
- 作者:jake
- 时间:2008-04
过去与未来在现在相遇
为什么一定要起这样一个很“拽”的标题?原因是,要理解生命自主运动就必须对时间这个概念进行深入思考,而这一点恰恰是目前的主流复杂性科学所严重忽略的一个问题。尽管有很多复杂系统模型都是动态的,但是要理解时间模拟是远远不够的。所以,我们必须重新发现蕴藏在系统之中的时间属性。
让我们再次从那个最一开始的问题:自主运动的小虫出发。当我们看到一只小虫按照它“自己的”意愿去觅食的时候,这意味着什么?把这个问题分解开来,应该是:
1、小虫在它自己的内部产生了一个目的或者叫意图:觅食;
2、在这个目的或者意图的驱使下,小虫觅到了食物把它吃掉,实现了这个目的。
对,就是这个“目的”使得我们可以区分出小虫和石子。正是因为小虫的运动是有目的的,所以它的运动才是一种按照它自己的目的进行的自主行为。反过来,石子的运动则完全是无目的的,所以它的行为就是被动的、非生命的。
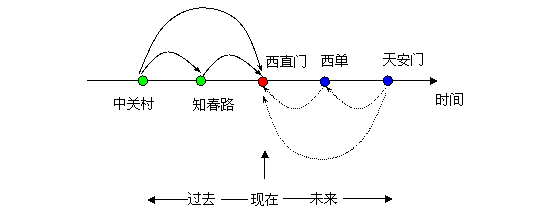
然而,究竟什么是目的呢?我们不妨从最简单的例子开始。假如你住在北京的中关村,想到天安门广场去玩。于是你会把天安门作为你的目的地,选择一条从中关村到天安门的乘车路线。显然,由于当时路面的情况,你会动态调整不同的路径,但是,无论选择何种路径,你的最终目的地不会改变。因此,在行进的过程中,你始终会用最终目的地作为对自己的指导选择路径。一个重要的事实是,天安门这个目的始终是你没有达到的,也就是说,你的目的存在于你想象中的未来世界,但同时这个未来的事物却影响了现在的你对路径的选择,也就是说你对未来的预期“影响了”你的现在。为了更加清楚起见,我们可以用一个时间轴图进行粗略表述:
以文中的实例出发,你从中关村乘车到天安门。假设现在你已经到了西直门(途经知春路),你的最终目的地是天安门,要实现这个目的,你需要先实现到西单这个子目标。图中的实箭头表示过去影响现在的因果关系(显然,你能到达西直门是受到过去的动作,从中关村到知春路的影响)。图中红点右侧部分属于未发生的未来世界,他们都是你头脑中假想出来的。虚箭头则表示一种目的(发生在未来的事件)对现在的隐含影响(因为目的是存在于未来并未发生的事件,而且是非主体的外在观察者看不到的事件,所以因果关系是隐含的)
非常抱歉,为了解释清楚生命的目的性,我不得不搬出诸如因果、时间等等这些形而上的哲学概念。如图3.1所示,我们看到从因果关系上看,过去和想象的未来对于现在的影响是对称的。一方面,过去的事情可以影响现在,离我们越远的事情对现在的影响越小越模糊。另一方面,未来的事情体现为行动主体的目的也会对现在造成影响,因为你要实现你的目的,你还会根据总目的规划出一些子目的来(如图3.1中的西单节点)。而且越远的事件(越大的目的)对现在的影响也越小。
然而,这种对目的和因果的解释一定不会被物理学家所接受,原因是物理学家永远都是一个冷酷无情的纯客观的观察者,他看到了你从中关村走到了西直门,并承认这样一种过去对现在的因果关系,但是他们决不会承认未来对现在的因果关系,原因很简单,他们不是你自己,所以他们并不知道你的目的所在。
为了解释目的,我们却遇到了一个更棘手的问题,即当我们从一个纯客观的角度来观察事物,例如活细胞的时候,我们如何知道它是有目的的呢?物理学家轻易不会承认未来决定现在这样的玄乎的因果关系,所以似乎我们的这种解释简直就是一派胡言。
慢着,也许我们低估了物理学家们进行哲学思考的能力了!从牛顿到爱因斯坦,真正的物理学大师一般都是精通哲学的大师!事实上,对于这种正向因果、反向因果、目的的讨论早已经成为一些物理大师们玩儿剩下的东西了,只不过我们的教科书从来没有这样表述而已。下面,且允许我用换个角度把我们熟知的一些东西重新表达一下。
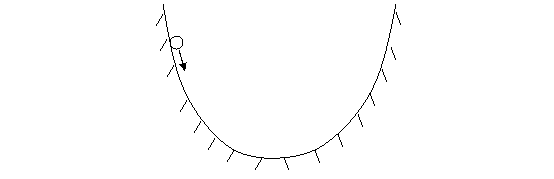
让我们先来看一个最简单的例子,如下图:
假设在一个粗糙的U形轨道上,有一个小球从侧壁滚下来。可以预料到,小球三晃两晃将会停在U字形的谷底。对这个物理现象最标准的解释应该是运用牛顿力学计算出小球每一时刻的受力,并根据上一时刻的位置和速度计算出下一时刻的位置和速度。如果从时间轴的角度看,这个过程显然遵循时间正向的因果关系。但是,这个计算过程太复杂了,物理学家发明了另一种更简单的方法。由于整个轨道位于一个重力场中,决定小球运动的也主要是重力,所以我们可以画出一条条等势线来,于是谷底也就对应了势能最小点。根本不用费力计算小球在每时刻的受力,物理学家就可以轻松地告诉你,小球一定停在最低点。这是因为,小球的运动将会使得势能最小化。当然这种表述是很客观、物理化的,我们稍微拟人、生动一点,可以把这个陈述表述为:小球运动的目的就是要最小化势能。
在物理中,用牛顿力学计算小球的运动轨迹和用最小势能来预测小球最终的位置都是同样正确的。然而这两种方法刚好用到了两种完全不同的因果律,前者是严格的正向因果,后者则是目的化的反向因果。因此,针对小球这个例子,我们可以完全对应到之前的中关村到天安门的例子上。只不过我们的教科书从来没有从目的论的角度来传授物理。
在物理中,虽然正向因果律和反向因果律是完全等价的,但是在很多场合下,用反向因果律(把物体的运动看作是有目的的)反而更加简洁、清晰。一个最好的例子就是费马的光行最速原理。
如图3.3,光线从A点投射到一个平面镜l上,反射到B点,问光线在哪一个点反射?这个问题很简单,按照反射定律,入射角等于反射角,我们很容易找到反射点O。然而,费马对于光的这条反射路径有一套完全不同的看法。他说,光之所以会走这样一条路径,是因为光要最小化它走过的路程。我们可以连接A点和平面镜l上的任意一点P,再连接PB,则这两条线段的总长度AP+PB当P到达位置O的时候刚好最小。而恰恰这条最短的路线就是光实际走的路线(我们不妨用初等几何验证一下)。事实上,在很多实际的复杂问题中(例如包括多个平面镜的反射,还有不同介质的折射情况),费马原理会比反射定律更容易求解。
停留在谷底的小球,走最短路径的光线,都向我们展示了没有生命的物体是如何寻求它们自己目的的。在日常生活中,我们还会遇到很多实际的优化问题,例如公司寻求利润最大化、个人寻求努力最小化等等,这些都是智慧生物的一种合目的行为。实际上,在数学家看来,追求目的和最优化某个数学函数问题完全就是一回事儿。原因就在于很多时候,那些能够描述清楚的目的总能够通过数学变化转换成一种优化函数。例如前面讲的从中关村到天安门的寻径问题,如果我们把地图上的任意点到天安门的距离看作目标函数的话,那么按照目的地寻找路径的问题就变成了对这个目标函数的优化问题了。
而我们更感兴趣的是针对一个客观系统的描述,客观系统会在时间之中演化。我们如何判断这个系统是否有目的呢?按照前面所说的优化问题和目的之间的关系,我们可以把目的转变成一个目标函数,于是如果说系统的演化是有目的的,那也就意味着目标函数存在着一个最小值或者最大值,系统演化的过程也就是使得目标函数值趋于最小或者最大的过程。因此,判断系统是否有目的的问题就可以转化为找到一个随时间而趋向最大或者最小值的函数的问题,并且该函数可以描述系统的状态。
如图3.5,用U型轨道中下落的小球为例,我们可以用小球所处位置的高度(或等价的势能)作为要找的描述系统状态的函数f,这样,小球的滚动过程被简化为f对t的曲线,而该曲线经过短时间内的震荡之后趋向于最小值了,此时小球停留在最低点。因此我们说小球的目的是要朝向这个最低点,它与最小化函数f是一样的。然而,光行最速原理的例子与这里的叙述略有不同,原因是光线经过APB的路径长度并不是系统状态和时间的函数,它是路径的函数。而且,在这里我们也看不到光线路径随时间的演化过程。对于这类有关运动路径的问题,我们将在后面进一步详细论述,这里不展开了。
总结来说,本章想要传达的主要信息是:目的、函数优化问题其实都是一回事儿,它们都反映了时间轴上未来事件对当前事件的影响。因此,在这个层面上,我们看到了系统演化、最优化等问题中的时间问题。