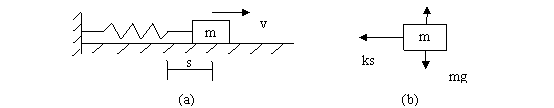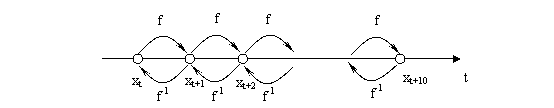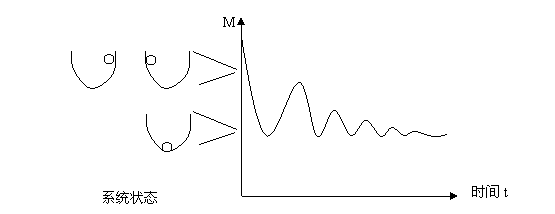生命之流(3)——牛顿力学2.0
- 作者:jake
- 时间:2008-05
牛顿力学2.0
虽然Autopoiesis理论从自我生产的角度给出了“生命软件”的一种广义描述,但是它却没有关注流动、能量、目的等生命系统中有关时间的概念。为了更透彻地理解它们,我们有必要走进物理的世界,看看物理学家们这几百年来是如何认识这些概念的。
让我们把记忆的时钟拨回到高中时代,在那时我们学到了牛顿力学。受力分析、运动分析、牛顿第二定律、问题求解几乎可以构成高中物理解题的几个标准步骤。如果我们把整个分析流程编制成计算机程序,那么只要输入初始位置、速度和边界条件等基本信息,该软件就会输出一个轨迹方程,它描述了任意时刻,系统所处的位置、速度等全部信息。时间t作为一个自变量就出现在系统输出的轨迹方程之中。这个方程就好比是一盒录像带,上面记录了系统未来的全部图景。你想获知100年之后系统的情况吗?没问题,只要你把录像带“倒到”100年那里就能看到全部你想要的图景了(相当于把[math]\displaystyle{ t=100 }[/math]年代如到了轨迹方程中)。为了使表达更加清晰,同时避免浪费过多的篇幅在细节上,我们将在框中给出一个具体的实例,读者可以有选择地跳过。
例1:
为了领略经典物理,让我们从一个非常简单的实例开始。
如图(a),一个物块(为简单,质量[math]\displaystyle{ m=1 }[/math]绑在一根弹簧上,在一个光滑水平面上往复运动,初始时刻物块位于位移[math]\displaystyle{ s=0 }[/math]的点,且初速度为[math]\displaystyle{ v_0 }[/math]。(b)为物块[math]\displaystyle{ m }[/math]的受力分析图,竖直方向重力和地面的支持力平衡,水平方向仅仅受一个向回拉的弹簧拉力,它的大小是[math]\displaystyle{ ks }[/math],其中[math]\displaystyle{ s }[/math]为弹簧伸长长度也就是物体的位移(将坐标原点取到弹簧的自然伸长处),[math]\displaystyle{ k }[/math]是一个常数,为了简单,设[math]\displaystyle{ k=1 }[/math]。
根据物块[math]\displaystyle{ m }[/math]的受力分析(图3.1(b)),我们可以写出制约[math]\displaystyle{ m }[/math]的牛顿第二定律方程:
其中[math]\displaystyle{ -s }[/math]就是物体所受到的合外力[math]\displaystyle{ F }[/math],[math]\displaystyle{ \frac{d^2s}{dt^2} }[/math]是物体的加速度[math]\displaystyle{ a }[/math],所以上式就是牛顿第二定律[math]\displaystyle{ F=ma }[/math]。这是一个关于位置[math]\displaystyle{ s(t) }[/math]的微分方程,代入初始条件[math]\displaystyle{ s(t)=0 }[/math],[math]\displaystyle{ s(t)'=v_0 }[/math],求解该方程,可得:
求一阶导数可得物块任意时刻速度:
这样,物块的全部信息(包括历史和未来)就都包含在这两个式子里面了。我们只要把[math]\displaystyle{ t=100 }[/math]代入(2)和(3)就能立即得知100秒后物块的位置和速度了。
然而,这种高中求解输出录像带的方法并不总能奏效。因为在有些时候,牛顿第二定律给出的微分方程可能非常复杂,以至于不能求解(并不是所有的微分方程都能给出显式解)。因此,我们有必要介绍第二种方法。早在19世纪,大数学家彭加莱(Poincare)为了证明有多个天体构成的太阳系系统是稳定的,专门发展了一套数学方法叫做动力系统。该方法既来源于早期的牛顿力学,同时又大大扩展了牛顿力学的应用范围,下面我们将主要探讨这种方法。
如果我们把之前讲的高中物理求解软件叫做牛顿力学1.0,那么动力系统方法就相当于是它的升级版本,所以称之为牛顿力学2.0。同样,你把系统的初始位置、速度等信息输入给它,它将给你输出结果。但是,与牛顿力学1.0最大的不同在于,2.0并不输出一盘记录系统全部未来信息的录像带,而是一个好玩的计算机模拟游戏。你想知道系统100年之后的样子吗?“可以,不过,对不起,您必须等到我一秒一秒地算到100年之后再说”,牛顿力学2.0回答道。
我们可以把牛顿力学2.0看作由两部分构成[math]\displaystyle{ \lt X,f\gt }[/math],其中[math]\displaystyle{ X }[/math]叫做系统的状态空间,[math]\displaystyle{ f }[/math]叫做演化规律。设在[math]\displaystyle{ t }[/math]时刻,系统的状态为[math]\displaystyle{ x_t\in X }[/math],那么在下一时刻系统的状态[math]\displaystyle{ x_t+1\in X }[/math]就将由下面的方程决定:
这样,只要我们给出系统在[math]\displaystyle{ t=1 }[/math]时刻的状态即[math]\displaystyle{ x_1 }[/math],我们就能通过(4)算出,[math]\displaystyle{ x_2=f(x_1) }[/math],[math]\displaystyle{ x_3=f(x_2)=f(f(x_1)) }[/math]……,等等全部信息。
对于一个物体来说,我们可以把它的位置[math]\displaystyle{ x }[/math]和速度[math]\displaystyle{ v }[/math]都看作是物体的状态。这样,该物体所处的状态空间就是[math]\displaystyle{ \{(x,v)\mid x\in R,v\in R\} }[/math]。演化方程(4)可以具体地从牛顿第二定律导出,请看下面的例子。
例1':
针对例1的情况,我们可以用牛顿2.0的方法再对它进行讨论。首先,如果设速度,那么可以把(1)式重新写为:
这样,原来的一个包含二阶导数的微分方程变成了两个一阶的微分方程。第一个方程实际上就是牛顿第二定律即加速度乘以质量等于合外力,第二个方程是速度的定义,即位置对时间的一阶导数。方程的右边可以看作两个变量:位置和速度的函数。这种左边是一阶导数,右边是函数的方程或者方程组就叫做微分动力系统(此处不展开讨论)。为了得到牛顿力学2.0的形式,我们把(5)离散化,即把该问题变为一个迭代程序。不妨设时间间隔[math]\displaystyle{ dt=0.0001 }[/math],这样(5)就变为:
这个方程就变成了一个离散动力系统的递推方程,它可以给出和方程(2)、(3)相近的答案(如果dt取得越小,则答案越接近)。
该系统的状态空间是(s,v)两个变量的所有可能组合,演化规律f是:
我们把初始速度和位置代入方程(即令[math]\displaystyle{ s_0=0 }[/math],[math]\displaystyle{ v_0=v_0 }[/math]),它就能算出新的[math]\displaystyle{ v }[/math]和[math]\displaystyle{ s }[/math]:[math]\displaystyle{ v_1=v_0 }[/math],[math]\displaystyle{ s_1=0.0001v_0 }[/math],再把这对新的值代入,得到:[math]\displaystyle{ v_2=v_0 }[/math],[math]\displaystyle{ s_2=0.0002v_0 }[/math],……。这样,虽然我们没有求解微分方程,但是仍可以用计算机一步一步地算出物块的位置和速度。在一般情况下,无论(5)能不能求解出来,我们都可以用计算机来求解(6),因此它具有更普遍的意义。
牛顿力学2.0也能够描述多个体的系统,只要我们适当扩大系统的状态空间就可以了。例如,我们考虑台球桌上的[math]\displaystyle{ n }[/math]个小球互相撞的系统,每个小球都可以用4个变量来表示[math]\displaystyle{ (x,y,v_x,v_y) }[/math],其中[math]\displaystyle{ x }[/math],[math]\displaystyle{ y }[/math]表示小球的坐标,[math]\displaystyle{ v_x }[/math],[math]\displaystyle{ v_y }[/math]表示小球沿水平方向和竖直方向的速度。那么[math]\displaystyle{ n }[/math]个小球就可以用[math]\displaystyle{ 4n }[/math]个变量来表示。所以系统的一个状态就是这[math]\displaystyle{ 4n }[/math]个变量的一种可能取值的组合,如[math]\displaystyle{ (1,3,0.2,0.3,2,1,0.1,0.2...) }[/math]就表示第一个小球的位置是[math]\displaystyle{ (1,3) }[/math],速度是[math]\displaystyle{ (0.2,0.3) }[/math],第二个小球位置是[math]\displaystyle{ (2,1) }[/math],速度是[math]\displaystyle{ (0.1,0.2) }[/math]……。这样状态空间[math]\displaystyle{ X }[/math]就被扩大成[math]\displaystyle{ 4n }[/math]维的空间了。系统的演化[math]\displaystyle{ f }[/math]也可以相应地写出来,但是这种情况下,给出类似(7)的数学表达式还不如直接写成计算机程序。
从计算机模拟的角度来看,系统的状态就相当于是存储于计算机内存中的数据,而系统的一步演化就相当于是计算机CPU的一次计算。这样,系统下一时刻的状态就可以用规律f作用到上一时刻的系统状态(数据)而得到。所以这样看来,很多计算机模拟程序,如细胞自动机、多Agent模拟系统都可以看作是牛顿力学2.0的特例。
因为计算机模拟程序并没有限制[math]\displaystyle{ X }[/math]和[math]\displaystyle{ f }[/math]是具体什么样的数据和程序,所以我们就可以进行大胆的抽象,设计出各种奇形怪状的模拟宇宙。我们完全可以让[math]\displaystyle{ X }[/math]中的元素变成桌子、烂袜子或者抽水马桶,[math]\displaystyle{ f }[/math]也并不一定非得是牛顿定律、量子力学,而可能是“魔兽世界”或者“第二人生”。数学对物理的抽象能够让我们再造出完全不同的“虚拟物理”!
牛顿力学2.0也能够描述多个体的系统,只要我们适当扩大系统的状态空间就可以了。例如,我们考虑台球桌上的n个小球互相撞的系统,每个小球都可以用4个变量来表示[math]\displaystyle{ (x,y,v_x,v_y) }[/math],其中[math]\displaystyle{ x }[/math],[math]\displaystyle{ y }[/math]表示小球的坐标,[math]\displaystyle{ v_x }[/math],[math]\displaystyle{ v_y }[/math]表示小球沿水平方向和竖直方向的速度。那么[math]\displaystyle{ n }[/math]个小球就可以用[math]\displaystyle{ 4n }[/math]个变量来表示。所以系统的一个状态就是这[math]\displaystyle{ 4n }[/math]个变量的一种可能取值的组合,如[math]\displaystyle{ (1,3,0.2,0.3,2,1,0.1,0.2...) }[/math]就表示第一个小球的位置是[math]\displaystyle{ (1,3) }[/math],速度是[math]\displaystyle{ (0.2,0.3) }[/math],第二个小球位置是[math]\displaystyle{ (2,1) }[/math],速度是[math]\displaystyle{ (0.1,0.2)...... }[/math]。这样状态空间[math]\displaystyle{ X }[/math]就被扩大成[math]\displaystyle{ 4n }[/math]维的空间了。系统的演化[math]\displaystyle{ f }[/math]也可以相应地写出来,但是这种情况下,给出类似(7)的数学表达式还不如直接写成计算机程序。
从计算机模拟的角度来看,系统的状态就相当于是存储于计算机内存中的数据,而系统的一步演化就相当于是计算机CPU的一次计算。这样,系统下一时刻的状态就可以用规律[math]\displaystyle{ f }[/math]作用到上一时刻的系统状态(数据)而得到。所以这样看来,很多计算机模拟程序,如细胞自动机、多Agent模拟系统都可以看作是牛顿力学2.0的特例。
因为计算机模拟程序并没有限制X和f是具体什么样的数据和程序,所以我们就可以进行大胆的抽象,设计出各种奇形怪状的模拟宇宙。我们完全可以让[math]\displaystyle{ X }[/math]中的元素变成桌子、烂袜子或者抽水马桶,[math]\displaystyle{ f }[/math]也并不一定非得是牛顿定律、量子力学,而可能是“魔兽世界”或者“第二人生”。数学对物理的抽象能够让我们再造出完全不同的“虚拟物理”!
虽然数学的确具有一定的“超越物理的数学实在性”,但是不可否认,具体的[math]\displaystyle{ X }[/math]和[math]\displaystyle{ f }[/math]会有不同的性质。那么这些不同性质的[math]\displaystyle{ f }[/math]和[math]\displaystyle{ X }[/math]究竟能够创造出什么样的物理呢?这是一个更加深刻的问题。
例如,如果[math]\displaystyle{ f }[/math]是个一一映射函数,那么该动力系统就是可逆的。当你看到一堆玻璃碴子自动从地面弹起聚集形成一个完整的花瓶,你一定知道这是电影在倒放!原因是,这个过程是不可逆的,即你能够很清楚地分辨出电影是正着放还是倒着放。然而,当你看到一个单摆上的小球不停晃动,就分辨不出来你所看到的是电影正放还是电影倒放。因为无论小球从左往右摆还是从右往左摆都是同等正确的(即符合我们观察到的常识)!那么这样的过程就是可逆的。(这两个例子是错误的,这里的可逆是计算的可逆性,与力学中的可逆性有很大的不同,为了后面讨论方便,可逆性都是指这里定义的计算的可逆性。多谢machine的指正!详见:http://www.swarma.org/swarma/detail.php?id=8158 )
[math]\displaystyle{ f }[/math]是一一映射意味着给定一个[math]\displaystyle{ x }[/math]数值,有一个唯一的数值[math]\displaystyle{ f(x) }[/math]与之对应。反之,给定一个数值[math]\displaystyle{ y }[/math],我们总能找到一个对应的[math]\displaystyle{ x }[/math],使得[math]\displaystyle{ f(x)=y }[/math]。这样,函数[math]\displaystyle{ f(x)=x^3 }[/math]就是一对一映射,而[math]\displaystyle{ f(x)=x^2 }[/math]就不是(因为给定[math]\displaystyle{ y=4 }[/math],我们既可以找到[math]\displaystyle{ f(-2)=4 }[/math],也可以找到[math]\displaystyle{ f(2)=4 }[/math])。如果[math]\displaystyle{ f }[/math]是一一映射函数,那么它的逆函数[math]\displaystyle{ f^{-1} }[/math]就必然存在。假设系统在10个时间步内的演化可以看作是从[math]\displaystyle{ x_t }[/math]经过[math]\displaystyle{ f }[/math]得到[math]\displaystyle{ x_{t+1} }[/math],再得到[math]\displaystyle{ x_{t+2},...x_{t+10} }[/math]的过程。那么反过来,从[math]\displaystyle{ x_{t+10} }[/math]开始,通过[math]\displaystyle{ f^{-1} }[/math]我们能够得到[math]\displaystyle{ x_{t+9},x_{t+8},...... }[/math]最后应用10次就可以得到[math]\displaystyle{ x_t }[/math],如图3.2。所以这个新的动力系统[math]\displaystyle{ (X,f^{-1}) }[/math]就是原系统[math]\displaystyle{ (X,f) }[/math]的逆系统,它所得到的过程[math]\displaystyle{ (x_{t+10},x_{t+9},...,x_t) }[/math]就是对过程[math]\displaystyle{ (x_t,x_{t+1},x_{t+2},...,x_{t+10}) }[/math]的回放。所以,我们说动力系统[math]\displaystyle{ (X,f) }[/math]是可逆的。
经典物理已经证明,从牛顿第二定律[math]\displaystyle{ F=ma }[/math]得到的动力系统都是可逆的。
在例1中,由于(7)式是个一一映射函数,因此它是可逆的,逆函数是:
这一点我们也可以从直观上看出来,实际上,物块朝右运动和朝左运动情况是完全一样的。
可逆动力系统没有我们常说的时间之箭,因为系统朝前演化和朝后演化是等价的,只要按照逆映射,我们可以从t+10时刻的状态完全恢复t时刻的状态。如果系统是不可逆的,那么系统就只能朝向时间的一个方向演化,因此,时间之箭的问题在动力系统中就明显突现出来了。
一般的[math]\displaystyle{ X }[/math]具有非常多的维度。例如,[math]\displaystyle{ n }[/math]个小球构成的台球系统的状态空间就有[math]\displaystyle{ 4n }[/math]维。考虑这么一个大维度的空间是很麻烦的,所以人们常常会将状态空间[math]\displaystyle{ X }[/math]进行压缩,即找到一个描述系统状态的函数[math]\displaystyle{ M(x) }[/math],让它在实数范围内取值(简称状态函数)来判明[math]\displaystyle{ X }[/math]以及动力系统的性质。因为系统的状态会在[math]\displaystyle{ f }[/math]的作用下不断发生变化,所以我们就能画出[math]\displaystyle{ M(x(t)) }[/math]随着时间的函数曲线。最常见的有几种情况:
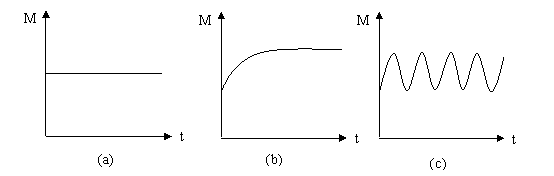
图3.3(a)表示状态函数随时间没有任何变化。例如,我们可以计算经典物理系统中的总机械能来作为函数[math]\displaystyle{ M }[/math],如果系统是忽略摩擦的,那么机械能就不随时间而变化,所以,我们也说能量是一个守恒量。
对于我们那个物块的例子来说,系统的机械能(势能+动能)是:
这是一个状态[math]\displaystyle{ x=(s,v) }[/math]的函数。因为状态在[math]\displaystyle{ f }[/math]的作用下会随着时间[math]\displaystyle{ t }[/math]不停地变化,所以有可能[math]\displaystyle{ E }[/math]也会随着时间变化。在这个例子中,我们能够求解(1)式得到[math]\displaystyle{ s(t)=v_0sin(t) }[/math]和[math]\displaystyle{ v(t)=v_0cos(t) }[/math],代入(4)式就得到[math]\displaystyle{ E(s,v)=\frac{1}{2}v_0^2(cos^2(t)+sin^2(t))=\frac{v_0^2}{2} }[/math]。我们看到总机械能是一个不包含时间的常数[math]\displaystyle{ \frac{v_0^2}{2} }[/math],这也就意味着能量是一个守恒量。
更一般的,只要我们能够找到一个从系统的状态空间[math]\displaystyle{ X }[/math]到1维实数空间[math]\displaystyle{ R }[/math]的映射[math]\displaystyle{ M:X \rightarrow {R } }[/math],使得[math]\displaystyle{ M }[/math]在[math]\displaystyle{ f }[/math]的作用下保持不变,即[math]\displaystyle{ M(x)=M(f(x)) }[/math],那么我们就找到了一个相应的该系统的守恒量。符合图3.3(a)的函数[math]\displaystyle{ M }[/math]都可以看作是系统的守恒量,例如在一些经典物理系统中,总动量或者总角动量就都满足这个性质。
图3.3(b)表示状态函数随时间不断增长并趋向一个固定值的情况。这说明系统的演化将趋向一类特殊的状态,这些特殊状态就好比是系统演化的“目的”或者“趋向性”。我们来看一个简单的例子(例2),如下图:
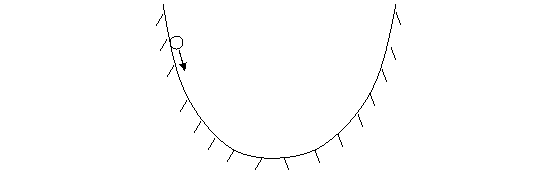
假设在一个粗糙的U形轨道上,一个小球从侧壁滚下来。可以预料到,小球三晃两晃将会停在U字形的谷底。对这个物理现象的解释当然可以用牛顿力学2.0求解,对式(4)那样的方程进行反复跌代必然会得到小球将停在谷底的结果。但是,这个计算过程太复杂了,我们还可以用一种不一样的方法求解出小球最后的平衡状态。由于整个轨道位于一个重力场中,决定小球运动的也主要是重力,所以我们可以计算小球的势能,于是谷底也就对应了势能的最小点。根本不用费力计算小球在每时刻的受力,物理学家就可以轻松地告诉你,最后小球一定停在最低点。这是因为,小球的运动将会使得势能最小化。进一步我们可以把小球具有的势能看作映射[math]\displaystyle{ M }[/math],那么我们不难画出[math]\displaystyle{ M }[/math]随时间变化的曲线,如下图:
虽然与图3.4(b)中的曲线略有不同,但是图3.5的曲线也将趋向于一个固定的数值,这一数值刚好对应小球所处的谷底状态。其实通过简单的数学变换,我们可以把趋向一个最小值的情况转变为趋向最大值的情况,如可以计算[math]\displaystyle{ -M }[/math]的曲线,这样就能得到与图3.4(b)相同的结果。图3.4(b)所表示的就是一个具有“目的性”的物理系统,因为我们可以拟人地说小球的目的就是为了让势能最小化。恰恰是可以利用系统的目的性,我们才可以直接计算出系统的平衡状态结果,而不需要更复杂的迭代计算。
假如这个例子中的小球在一个光滑的曲面上滚动,那么如果再次画出小球势能同时间的关系就能得到类似图3.4(c)中的结果。这种结果在很多具有周期行为的系统中都很常见。图3.4(a)和(c)这两种情况都显示出系统的行为对时间的某种对称性。(a)情况为一个与时间无关的状态函数,在时间轴上就相当于是处处对称的。(c)则是关于时间平移对称的,只要我们在时间轴上平移固定的周期长度,那么我们将不能分辨时间点。而只有在(b)这种情况下时间才是系统的一个本质属性。因为随着时间的流逝,系统会趋向一个比较明显的“目的”。这样根据趋向该目的的程度不同,我们就能分辨出系统处于不同的时间点上。而且,时间的方向性也可以在这种情况下被分辨出来。假如时间反演,我们会看到系统的状态函数M将从一个数值开始发散出来,它的行为和正向演化是非常不同的。
总结来看,利用牛顿力学2.0的方式描述系统的演化具有更加抽象的数学形式。我们可以讨论具有不同数学性质的动力系统而得到不同的虚拟宇宙。虚拟宇宙中有关时间的属性就全部体现在X和f的数学性质之中了。玩过游戏的人都知道,一般的游戏世界跟我们的现实世界一样是时间不可逆的,死掉的超级马莉不可能再从坑里跳出来去采蘑菇。但是我们可以通过保留虚拟世界每一时刻的状态(相当于把状态空间[math]\displaystyle{ X }[/math]扩充以便系统可以存盘),让动力系统的[math]\displaystyle{ f }[/math]变成一个一一映射函数(即在游戏的演进过程中并不丢失任何信息),这样就能让系统变成可逆的。
给虚拟宇宙添加守恒的物理量可以让它的演化体现出一种时间上的平衡性,如在游戏世界中添加总守恒的财富就可能让系统变得更加平衡,因为它在时间上是对称的。而如果我们能够找到一个如图3.3(b)所示的状态函数,就能够预测出动力系统演化的平衡属性,因为系统将自发趋向于那个状态。所有这些讨论都不仅可以帮助我们更加深刻地认识我们所处的现实宇宙,而且还可以帮助我们设计不一样的虚拟世界,更重要的是它帮助我们从一种更加抽象的角度来认识时间。