计算力学

计算力学（Computational Mechanics）是一套数学框架，试图从历史序列的形态（Morph）系综中寻找、总结规律，并预测未来。“寻找、总结规律、预测未来”属于“智能活动”的一种，在许许多多的“智能活动”背后又有着潜在的更一般的规律。潜在的一般的规律，往往来源于对微观态进行粗粒化形成宏观态的因果涌现。计算力学从信息论出发，采用计算的视角，定义出模式，因果态，各态之间的转换等重要概念，并最终将“智能”抽象为支持通用计算的ϵ-机器。ϵ-机器被有关学者从理论上证明，有着宏观态上的信息封闭性和计算封闭性，可以展现出极大的预测能力和极小的复杂性。ϵ-机器有序对的因果态对所有长度未来[math]\displaystyle{ \overset{\to}{S} }[/math]而言还有着强同质性（Strict Homogeneity of Causal States）。

问题背景

自然和社会现象

复杂系统的涌现问题由来已久。最吸引人的和使人迷惑的自然模式是那些在高度结构化的联合行为随着时间涌现于简单子系统的交互。鸟群以步调一致地形式飞行，鱼儿在没有领头带领以连贯的序列群组流转并突然共同转向的方式游动。蚊群形成复杂的社会，生存继承自特异化的社会分工，不是由中心领导所带领。几个世纪前，木星大气中五彩斑斓的混沌运动形成了被称之为“大红斑”的巨大漩涡，至少已存在二百到三百五十年，期间还在不断地改变颜色和形状。出现在经济系统中商品价格优化从主体服从本地商业规则中浮现。甚至在明显复杂系统处理玩家关键角色涌现全局信息。比如说，人类对场景中一小块颜色的感知，会依赖于整个场景的颜色成份，不仅仅在于对空间局部视网膜检测器对频谱的反应。类似地，外形的感知可以由全局拓扑属性被增强，比如曲线是开放还是封闭。

全局坐标如何在这些过程中涌现？普通的机制能引导多样现象的涌现吗？同时代的科学和数学能提供什么语言去精确地描绘这些系统中涌现的不同组织？

涌现通常被理解为一个引导结构出现的过程，该过程不能直接由定义约束和控制系统的即刻作用力所描述。随着时间的推移“一些新东西”在某尺度出现，且不能由运动的等式所说明。一个涌现的属性也不能明确由初始和边界条件所表征。简而言之，当下层系统释放一些效应到它的创建中则一个属性涌现。

这些观察构成直观的涌现定义。为了让它更可用，无论如何，得有人说明“那些东西”是什么，并且它“新”在哪里。否则，表述就很少，甚至没内容，因为几乎所有时间相关系统将展现涌现属性。

现象的计算视角

人们在生产生活中所用的计量方法及科学家们的计算机理论模型和实际计算设备。由于理论上已经证明图灵机、通用图灵机、元胞自动机、神经网络是计算等价的，所以计算力学词条选择一个等价关系来展开讲。这些计算包括算术方法和数理逻辑。

使用适当的假设和划分方法，在科学领域也称为映射，在复杂科学里则称为粗粒化，能够获取一定程度上计算的下列特性：

• 封闭（完备）性。
• 一致性。

我们取智能体对环境的适应度为指标，可将绝大多数项目整理出层次性，数据和逻辑，从而纳入计算力学数学框架，进而使其和环境共同演化。

计算复杂度理论

问题有以下特征引发了计算复杂度理论

• 非常长的输入和输出，但仍然有限；
• 理论上有无限长的历史和未来；
• 确定性系统也会引发混沌；
• 系统存在可遍历和不可遍历的区分；
• 无限长序列也存在数量上的大小关系；
• 拯救2050奇点临近。

由于这些计算问题带有较高的复杂性，因此引入复杂系统和复杂网络高阶网络超图流网络网络渗流等基本术语，及所解决问题的一些分类。

在牛顿力学提出以后，掀起了一轮科技工业革命，人们逐渐走向科学时代，对自然现象有了全新的理解。一些现象可以解释为物体间力的相互作用，且物理学家们对作用力的大小和物体状态的改变建立联系，使用方程的形式来表达。自此人们对自然的认识空间的进步，遇到很多现象也不再迷茫，能够更多地把握事物的运动规律。这种力的相互作用，表现形式十分多样，物理学家们做了一些基本的分类。这些分类一般基于相应的科研成果，再归类到原子层面的效应原理。科学家们基于这些成果，做了大量的观测和研究，不断发现力的大小随距离远近发生变化，变化的趋势和范围都跟元素周期和同位素有关。

然而这只是元素级别的力学现象，这些现象出现在元素级别，并不能完全反映到另外的级别，比如我们在不借助电子显微镜，只借助人眼的条件下进行观测，很多现象不能简单地归结为元素间的相互作用，或者说很难用元素间的相互作用，来直接表现宏观层面的相关模式。比如在水里组团游动的鱼群，他们的游动方向很难用各自的距离保持这个因素来表示。再比如生物圈，从山水林田湖草沙，到羊牛蚊蝇兔狗猪，都很难从单个物种来做一些属性判别。这时往往需要借助新的科技手段，来对这些模式进行深入研究，发现其潜在的原理和规律。

一般对涌现现象定义为不能简单归结为元素间的相互作用力，而需要从对应层面来描述的现象，认为是涌现。如果建立了促成这种涌现现象发生的机理的算法模型，则细化为因果涌现，是随附了宏观动力学的一类涌现。这种涌现往往比微观层面更强，在Erik Hoel的理论框架中，用有效信息EI来度量因果涌现效应的强弱。在计算力学框架中，则在某些层面将“新颖”就归结为“涌现”，而这些新颖的东西就是需要在旧有的理论框架上做补充，或者要么建立新的框架。新颖的东西能在因果涌现框架上不断地出现，最终能被宏观动力学方程[math]\displaystyle{ \Phi(x) }[/math]和计算力学原理所捕捉。

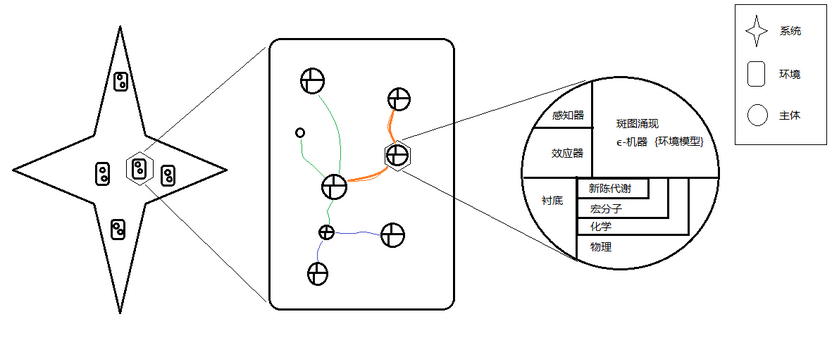
自然界中（Nature）或宇宙（Prototype Universe）中总是处在不断变化之中，这也是相对的。在这种相对变化的环境中，可能出现确定性或稳定性，导致观测者可以被存在。这时观测者和特定的稳定环境出现相互依赖，观测者对特定环境之外投入的关注视情况而定。观测者对该稳定环境中出现的微扰会加以关心，直到微扰变得可测量且足够充分，超过某一阈值，使得群落对该现象都表达过关心。达到相变程度后，涌现现象即产生，但群落中的观测者对相变后的环境仍会继续观测，改变内生涌现斑图，或启动单个或群落的效应器，使得环境的多个指标重新落入某个范围。这种差额机制(co-relation)即可用于对比，也可用于对齐。

自然存在是一个世界，主体（观察者）是世界的子集的同时，主体也会在内部构建一个世界的映象。这个过程本身从定性上来讲，也是一种涌现现象。计算力学选择建立从自然到主体，再从主体到涌现（头脑风暴），最后主体增加适应性的角度来阐述关系。

在计算力学理论框架中，有关的文献将极大的环境称为宇宙，其下是环境和智能体。本篇文章中，将原始文献的三级模型压缩为二级，将宇宙和环境整合成新的环境，以方便使用二分法。经过这种整合后，自然世界被划分成环境和智能体，分别嵌入确定性动力系统和随机动力系统。智能体（Agent）是一类观测者（Observer），能从自然界涌现出的斑图解析出来，从而得到智慧，进而改善智能体内部对环境的模拟，从而不断提高适应性。如果智能体对环境斑图的解析是正确的，则这种解析计算能力可能会被加强，使对环境的适应性呈现增强的状态。

上述对涌现和观测者的描述会遇到一定的困难，或者说削弱了斑图涌现的含义。如果我们认为斑图被观测者A识别，然后当成涌现，固有的内在涌现就难以定义了。为了解决这个困难，我们使用一些形式化方法，将环境中斑图的涌现当成“The emergence of pattern”，而将智能体A识别的涌现当成“The emergence of pattern”的相，即“The emergence of pattern in Agent A”。这个“The emergence of pattern in Agent A”将会塑造“Agent A”，也可能会成为“Agent A”的序参数，使得“Agent A”内部不断强化这个相。当将视角转向世界模型中的其他观测者（也可能是智能体），比如智能体B，它除了能捕捉环境中的“The emergence of pattern”外，还会发现被“The emergence of pattern in Agent A”塑造过的“Agent A”，而被塑造过的“Agent A”因为有了序参数，而本身又成为一种涌现的斑图，存在于智能体B的环境中。

所以在计算力学中，涌现的关系形式化为：涌现的斑图EP，被观测者A，即智能体A，捕捉成[math]\displaystyle{ Image_{an} = Agent_a(EP) }[/math]，从而塑造[math]\displaystyle{ Agent_a }[/math]为[math]\displaystyle{ Agent_a(Image_{an} = Agent_a(EP)) }[/math]。同时涌现的斑图EP，也会被智能体B，捕捉成[math]\displaystyle{ Image_{bn} = Agent_b(EP) }[/math]，而智能体A的固有涌现[math]\displaystyle{ Agent_a(Image_{an} = Agent_a(EP)) }[/math]也被智能体B识别成[math]\displaystyle{ Image_{ba} = capture(Agent_a(Image_{an} = Agent_a(EP))) }[/math]，使得智能体B成为[math]\displaystyle{ Agent_b(Image_{bn} = Agent_b(EP), Image_{ba})) }[/math]。这种形式化仅考虑了映射的输入和输出，具体的智能体的随机动力学会在相应部分展开。

在这里，我们可以有下列术语：

• Nature，缩写为n，即环境。
• Agent，智能体，可以有多个，其序号用下标表示。
• Capture，智能体对斑图涌现的进行识别。
• Image，智能体对斑图涌现的识别出的相，可以认为是智能体知识体系中的一条规则。下标为哪个智能体捕捉谁的斑图。

一个环境和多个智能体形成的复杂网络，涌现的斑图有些无法从两两关系中得出。

自然环境中各元素涌现出的斑图，经物理极微观态通信信道被智能体识别，智能体启动内因检查，增强或削弱内生斑图，然后完成理想目标的模拟，满足群落计算的完备性（Closure），形成计算和信息的流网络，促进智能体的完整适应，可作为计算力学形式化的优化目标之一。计算力学的结构来源于统计，产生于二分计算，自然环境为持，真空环境为拓。有了对比就有了“新颖”和“不适”，智能体初始只能选自然环境。在检测到位于边缘时，启动警示和调节机制，将自己拉回到自然环境。当群落形成时，计算中可舍弃部分微观态的历史，使得稳定发展成为主流，从而时刻准备着完成更高阶的完备性。

第0阶的完整性可以说是维持自己存在于自然环境，这种完整性信息输入和能量消耗极小，这几点可以形成计算的结构和导致斑图的涌现。

由于扰动的存在，形式语言的字符串很少单独出现在环境中，所以除了智能体的识别涌现斑图外，还有将其他智能体拉回微扰的智能体和机制，使得能在混沌动力学中找出周期的存在，智能体各方面保持相对稳定性。

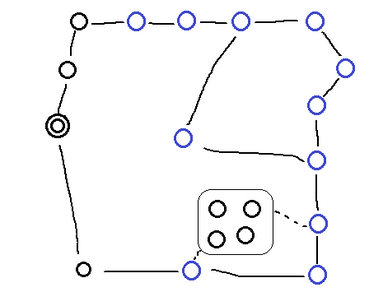
如上图所示，为某种有源没有汇的能量流网络，微观上起始点为双环处，能量在实线处流动。当宏观上的条件满足时，矩形框处的功能将随宏观上的需求情况进行变化，造成某些层次的斑图涌现。涌现出的斑图在很多层次都不可预测。在计算资源有限的条件下，4个子节点的功能，以开关形式表达，可以形成2⁴=16种不同的数字形式。我们可以对矩形框处的功能做以下假设：

• 形成汇节点
• 用于对相关节点逻辑进行粗粒化
• 存储循环节的长度

计算的封闭性也可以看作是斑图，是一种涌现现象，这种机制和形式化在集智俱乐部公众号文章《从生命到星系，新数学揭示大尺度秩序如何涌现》做了更详细的阐述。在上图中理解上需要做的突破或证明的是，在微观层面上，能量也从实线处流过，也可以从虚线处流过，但在经过粗粒化后，宏观态的功能可以维持不变。计算力学提供了判断哪些具有层级结构的标准，并且可以在多个实例模型上进行测试。牛顿力学起初可以解决2个刚体之间的问题，因果关系也变得非常明确，这种计算的封闭性和对称性展现了科学之美。到了液体和气体，我们使用体积和压强来表示，这时的“因果关系”我们更愿意称其为“理想状态下”的宏观性质。很多学者在深入了解液体和气体的机制时，发现了布朗运动，最终通过该渠道引发了“原子”这个概念的涌现。于是科学家们在“原子”层面实现计算的封闭性，愿意称其为“粒子”，维持着科学的基本地位。这些“粒子”层次的运动仍遵循相应的力学属性，简单使用牛顿力学会使得计算量非常庞大。计算力学的算法努力尝试找到因果态层次的封闭性，使得复杂度极小且预测性极佳。

综上所述，新东西即能在现有流网络上产生，也能在微观态上兴趣点的平坦或极值处产生。计算力学尝试同时解决平庸和复杂的问题，在智集百科里，我们主要集中于复杂问题的描述的解决，并由此突出统计复杂度的重要性。

计算复杂度

二值计算

01 二分法 简易 困难 平凡（平庸）灵活

二项式分布 正态分布 泊松分布

共轭根式

二元一次方程 [math]\displaystyle{ ax^2+bx+c=0 }[/math]的根式解为：

[math]\displaystyle{ x_1 = \frac{-b+\sqrt{b^2-4ac}}{2a}, \ x_2= \frac{-b-\sqrt{b^2-4ac}}{2a} }[/math]

根的判别式为[math]\displaystyle{ \Delta = b^2-4ac }[/math]

仔细研究求根公式，可知二元一次方程通常有2个根式解，

• 在根的判别式Δ>0时，二次一次方程[math]\displaystyle{ ax^2+bx+c=0 }[/math]有两个不相等的实数根
• 在根的判别式为Δ=0时，两解相等，
• 在根的判别式Δ<0时，没有初等解。

再仔细分析Δ>0的情况，二次一次方程[math]\displaystyle{ ax^2+bx+c=0 }[/math]的两个根中，表达式可以写成分式，可知这两个根为有理数。分母均为2a，分子前面部分均为-b，中间差一个正负号，为共轭根式的一个实例。分式借助集智百科平台，显示成二维屏幕上的像素点，其实内部存储的源代码，是一维字符串，两个根只差一个符号。由于两根都是解，任取一根都可使二元一次方程成立。在我们的转移示例中，可使[math]\displaystyle{ 符号'0'=x_1,符号'1'=x_2 }[/math]，这样的“01”字符串便可使某表达式成立，也可以在两端进行延伸。

柯式复杂度

柯式复杂度是大家公认的复杂度度量方法，在Jean-Paul Delahaye和Hector Zenil对复杂系统量化方法研究的工作中，认为最天然的计算设备的模型需要有一定的表达能力，并定义是一个字符串s对于通用图灵机U的柯尔莫哥洛夫-蔡汀(Kolmogorov-Chaitin)复杂度[math]\displaystyle{ K_{u}(s) }[/math]为输出该字符串s的最短程序p的二进制长度。

[math]\displaystyle{ K_{u}(s) = min\{\lvert p \rvert, U(p) = s \} }[/math]

下标u是对应图灵机的代号。

柯式复杂度的主要缺点是因为停机问题而导致的不可计算性，针对K式复杂度的主要评论是它高度依赖编程语言的选择。

为提高通用性，忽略各图灵机之间的差异，将柯氏复杂度定义进一步定义为：

[math]\displaystyle{ K(s) := C_U(x) = min\{ \lvert \lang M,w \rang \rvert: 图灵机M在输入w时停机并输出x \} }[/math]

按照前式标准化为：

[math]\displaystyle{ K(s) := C_U(x) = min\{ \lvert \lang M,w \rang \rvert: M(w) = x \} }[/math]

这里的w等于前式的p，即输出x的程序源代码字符串。

在文献中确定柯式复杂度的定义时，使用了两种不同的计算模型：

• 确定性图灵机（deterministic Turing machines (TM)）
• 一维元胞自动机（CA）

做了计算性能的比较，实验结果显示两者有着很强的相互关联，而且两者均依靠输出字符串反转和计算对称性来进行分组。

统计复杂度

定义及符号[math]\displaystyle{ C_{μ} }[/math]

μ依赖于测度和分布

统计复杂度可用于线性系统的复杂性量化，也可用于非线性动态系统中复杂系统因果涌现复杂性的量化。香农熵基于概率分布，但对于确定性混沌却有些不足，统计复杂度则能量化宏观态上出现的确定性混沌。

统计复杂度（statistical complexity）是复杂系统深度的量化方式之一，用[math]\displaystyle{ C_{\mu} }[/math]符号来表示。其中μ依赖于测度和分布。跟统计力学中的量化理论有关，基于测度系统的定义。在部分混沌物理学的文献中，也被记作α。

在1989年《Inferring Statistical Complexity》这篇文献里，复杂度的阶次符号为α，在2001年《Computational Mechanics: Pattern and Prediction, Structure and Simplicity》中的符号为μ，这里我们统一使用μ。

μ-阶图复杂度

μ-阶图复杂度即为μ-阶图的概率算术复杂度，[math]\displaystyle{ C_{μ=0}=\log \lvert \mathbf{V} \rvert }[/math]。其中[math]\displaystyle{ \mathbf{V} }[/math]为μ-阶图的顶点集合。

在集智俱乐部的《因果涌现读书会》因果几何上，会对连续系统的因果涌现做更详细的介绍，有兴趣的可以参考下。

0-阶图复杂度([math]\displaystyle{ C_{μ=0} }[/math])和蔡汀-柯尔莫哥洛夫复杂度不同，0-阶图复杂度带有概率分布且依赖带有随机整数寄存器的图灵机。

μ-阶图复杂度（[math]\displaystyle{ C_{μ} }[/math]）是区别于信息论的量化复杂度的方法，后者基于维度[math]\displaystyle{ d_μ }[/math]和熵[math]\displaystyle{ h_μ }[/math]。

拓扑复杂度

当μ-阶图复杂度的μ为零时，μ-阶图复杂度也称为拓扑复杂度。由ϵ-机器的物征值给出。

统计复杂度

μ-阶图复杂度的μ = 1时，复杂度的量化方式为统计复杂度，带有热力学的“高温限制”。这里的统计复杂度也是1-阶图复杂度，即为香农熵。由ϵ-机器的物征向量给出。 统计复杂度（statistical complexity）是复杂系统深度的量化方式之一，用[math]\displaystyle{ C_{\mu} }[/math]符号来表示。这里的对应于因果涌现量化（有效信息EI），统计复杂度[math]\displaystyle{ C_{\mu} }[/math]越小，有效信息EI越大。

统计复杂度的下界，从周期行为和频段耦合中得出，是带二阶项的相位转换。

复杂度优化

经过演化，因果链能形成形式上的闭环，这里闭环在后文的因果态里，是指因果态在所有有效态中，统计复杂度最小等特征和属性。在管理学中，类似于使用组织行为学的知识，构建特定的反应链，从而完成特定目标。

因果态

因果态的定义

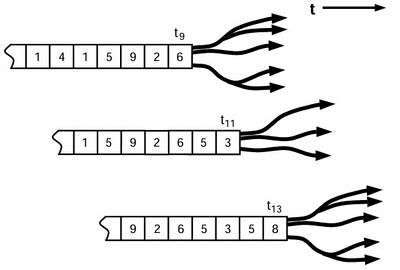
因为智能体的测量装置精度都是有限的，在读取外部环境的测量结果时一般为时间序列上的离散值。测量结果中的某个测量值可能对应某个“隐藏”状态（“隐藏”状态是智能体存储于其内部环境中的已知状态）。若在离散时间序列上不同的测量值对未来的预测有相同的模式，都对应一个相同的 “隐藏”状态，那么，将这个“隐藏”状态称作这些不同测量值的因果态（casual state）。

如上图所示，在[math]\displaystyle{ t_9 }[/math]和[math]\displaystyle{ t_{13} }[/math]时刻分别对应一个状态，这两个状态处于相同的因果态，因为对未来的预测具有相同的分布；在[math]\displaystyle{ t_{11} }[/math]时刻的状态，则与[math]\displaystyle{ t_9 }[/math]和[math]\displaystyle{ t_{13} }[/math]时刻处于不同的因果态。

因果态的形式化定义可以按照如下方式描述：

将测量的数据流[math]\displaystyle{ s=⋯s_{-2} s_{-1} s_0 s_1 s_2… }[/math]分为两个部分，按照时间[math]\displaystyle{ t }[/math]分为前向序列[math]\displaystyle{ s_t^→=s_t s_{t+1} s_{t+2} s_{t+3}… }[/math]和后向序列[math]\displaystyle{ s_t^←=⋯s_{t-3} s_{t-2} s_{t-1} s_t }[/math]，可以得到一个单侧前向序列和一个单侧后向序列，它们分别表示[math]\displaystyle{ s_t }[/math]关于未来和过去的信息。

属于相同因果态的两个状态[math]\displaystyle{ t }[/math] 和[math]\displaystyle{ t^{'} }[/math]，他们之间的关系可以表示为：[math]\displaystyle{ t∼t^{'} }[/math]，“[math]\displaystyle{ ∼ }[/math] ” 表示由等效未来形态所引起的等价关系。那么，就会有如下关系：

   [math]\displaystyle{ t∼t^{'} }[/math]定义为[math]\displaystyle{ Pr(s^→ |s_t^← )=Pr(s^→ |s_{t^{'}}^← ) }[/math]

[math]\displaystyle{ Pr(s^→ |s_t^← ) }[/math]和[math]\displaystyle{ Pr(s^→ |s_{t^{'}}^← ) }[/math]为[math]\displaystyle{ s^→ }[/math]的条件概率分布，式中序列[math]\displaystyle{ t }[/math]和[math]\displaystyle{ t^{'} }[/math]通常是不同的，如果生成数据流[math]\displaystyle{ s }[/math]的过程是遍历的，上式可以理解为，如果[math]\displaystyle{ t∼t^{'} }[/math]，就算在不同时刻测量到了不同状态，智能体对未来状态的预测结果也会是相同的。

因果态的主要性质

将所有历史序列的集合记作[math]\displaystyle{ \overset{\leftarrow}{S} }[/math]，将[math]\displaystyle{ \overset{\leftarrow}{S} }[/math]按照某种函数映射方法划分为若干个互斥且全面的子集，那么每个子集就是一个有效态（effective state），这些有效态的集合记作[math]\displaystyle{ \mathcal{R} }[/math]，进一步理解其实有效态就是将[math]\displaystyle{ \overset{\leftarrow}{S} }[/math]中的某段序列粗粒化后得到的宏观态。按照最优的划分方法得到的有效态就是因果态，这些因果态的集合记作[math]\displaystyle{ \mathcal{S} }[/math]，[math]\displaystyle{ \mathcal{S} }[/math]是[math]\displaystyle{ \mathcal{R} }[/math]的一种最优形式，那么为什么[math]\displaystyle{ \mathcal{S} }[/math]是[math]\displaystyle{ \mathcal{R} }[/math]的最优形式呢，因为[math]\displaystyle{ \mathcal{S} }[/math]的如下性质。

（1）在相同统计复杂度的前提下，因果态集合[math]\displaystyle{ \mathcal{S} }[/math]在有效态集合[math]\displaystyle{ \mathcal{R} }[/math]的所有类型中，它的预测能力最强，用公式表示为[math]\displaystyle{ H[\stackrel{\rightarrow}{S}^L|\mathcal{R}]\geq H[\stackrel{\rightarrow}{S}^L|\mathcal{S}] }[/math]，[math]\displaystyle{ \stackrel{\rightarrow}{S}^L }[/math]为[math]\displaystyle{ L }[/math]个长度的未来序列集合，[math]\displaystyle{ H[\stackrel{\rightarrow}{S}^L|\mathcal{R}] }[/math]和[math]\displaystyle{ H[\stackrel{\rightarrow}{S}^L|\mathcal{S}] }[/math]是[math]\displaystyle{ \stackrel{\rightarrow}{S}^L }[/math]的条件熵。

（2）在相同预测能力的前提下，因果态集合[math]\displaystyle{ \mathcal{S} }[/math]在有效态集合[math]\displaystyle{ \mathcal{R} }[/math]的所有类型中，它的统计复杂度最小，用公式表示为[math]\displaystyle{ C_\mu(\hat{\mathcal{R}})\geq C_\mu(\mathcal{S}) }[/math]，[math]\displaystyle{ \hat{\mathcal{R}} }[/math]与[math]\displaystyle{ \mathcal{S} }[/math]有同等的预测能力，满足[math]\displaystyle{ H[\stackrel{\rightarrow}{S}^{L}|\hat{\mathcal{R}}]=H[\stackrel{\rightarrow}{S}^{L}|\mathcal{S}] }[/math]。

上文中已经介绍了柯式复杂度和统计复杂度的基本概念，如果[math]\displaystyle{ s^L }[/math]表示对过程的测量结果的前[math]\displaystyle{ L }[/math]个序列，那么它们之间的关系可以近似的表示为：

[math]\displaystyle{ K(s^L )≈C_μ (s^L )+h_μ L }[/math]

如果在已确定描述语言（程序）的情况下，柯式复杂度[math]\displaystyle{ K(s^L ) }[/math]可以理解为描述[math]\displaystyle{ s^L }[/math]所用的总信息量。

[math]\displaystyle{ h_μ }[/math]为香农熵率，是信息不确定性程度的归一化指标，信息的不确定性越高，香农熵率越大。[math]\displaystyle{ h_μ }[/math]在这里可以理解为误差率， 则[math]\displaystyle{ h_μ L }[/math]为允许损失的随机信息量。

统计复杂度[math]\displaystyle{ C_μ (s^L ) }[/math]可以理解为允许存在误差率[math]\displaystyle{ h_μ }[/math]的情况下，描述[math]\displaystyle{ s^L }[/math]所用的最少信息量。

结合本条性质，求[math]\displaystyle{ C_μ (s^L ) }[/math]就是求[math]\displaystyle{ s^L }[/math]对应的因果态的统计复杂度，也就是说想要计算[math]\displaystyle{ C_μ (s^L ) }[/math]需要先找到[math]\displaystyle{ s^L }[/math]对应的因果态。

那么公式可以解释为：序列[math]\displaystyle{ s^L }[/math]的总信息量≈被归纳的因果态信息量+放弃归纳的随机信息量

（3）在相同预测能力的前提下，因果态集合[math]\displaystyle{ \mathcal{S} }[/math]在有效态集合[math]\displaystyle{ \mathcal{R} }[/math]的所有类型中，它的随机性最小，用公式表示为[math]\displaystyle{ H[\hat{\mathcal{R}}^{\prime}|\hat{\mathcal{R}}]\geq H[\mathcal{S}^{\prime}|\mathcal{S}] }[/math]，[math]\displaystyle{ \hat{\mathcal{R}} }[/math]满足[math]\displaystyle{ H[\stackrel{\rightarrow}{S}^{L}|\hat{\mathcal{R}}]=H[\stackrel{\rightarrow}{S}^{L}|\mathcal{S}] }[/math]，其中[math]\displaystyle{ \hat{\mathcal{R}}^{\prime} }[/math]和[math]\displaystyle{ \mathcal{S}^{\prime} }[/math]分别是该过程的下一时刻有效态和下一时刻因果态。

用互信息的角度去理解的话，上式等价于[math]\displaystyle{ I(S^{\prime};S)\geq I(\widehat{R}^{\prime};\widehat{R}) }[/math]，可以理解为任意有效态对它自己下一时刻的互信息中，其中因果态的互信息最大，若不考虑Do干预，因果态和因果涌现理论中最大化有效信息所得到的宏观态意义相同。

若想更深入的理解因果态的性质可以阅读James Crutchfield的两篇论文，里面有因果态更多的性质和对应的形式化证明过程。

厄普西隆机器

厄普西隆机器（ϵ-machine） 此机器可以有效捕获模式，形式为有序对[math]\displaystyle{ \left \{ \epsilon, \mathbf{T} \right \} }[/math]。可以是信息源的生成机器，也可以是信息目的地重构出的机器。

ϵ-机器和图灵机不同，简单的图灵机是一种完全抽象的计算模型，它被实例化为冯·诺依曼架构，是现代计算机的理论模型。ϵ-机器可以通过和环境的互动，不断理解环境，更新自己的内秉属性，引入固定和随机变量而重构出来。

无限判定厄普西隆机器（ϵ-machine）可以表征为有限版本，并通过后续章节的重构算法形成字符生成器。

层次机器

多尺度

层次机器由多层ϵ-机器构成，其中单层ϵ-机器停留在水平因果态。层次机器从特定视角来看，是ϵ-机器的一个变体，是垂直方向的因果态。

层次机器具有多尺度自动建模的能力。

重构算法

1. 在最低水平上，设定0级模型为描述数据本身，即M₀=s₁s₂s₃...；

2. 从更低模型重构模型M_l=M_l-1/~，其中~表示l级上的因果等价类；操作的含义是，在l-1级上被区别对待的状态在l级上可以被视为同一个因果态。此时S和T都更新了；

3. 收集更多的数据，增大序列长度L，得到更加精确的一系列模型M_l；

4. 如果随着L增大，模型的复杂度发散，即[math]\displaystyle{ \lVert M_l \rVert \to \infty }[/math]，那么回到第二步，得到更高级模型M_l+1；

5. 如果模型复杂度收敛，意味着重建好了一个合适的ϵ-机器，程序退出。

实例

逻辑斯谛映射

逻辑斯谛（Logistic）映射求取迭代函数的极值，此极值可能呈现单周期、倍周期等现象。

元胞自动机

元胞自动机的复杂度的量化可使用0-阶图复杂度，即算术复杂度。

编者推荐

计算力学和因果涌现关系密切，计算力学借鉴了因果涌现大量的概念、算法以及模型，并提出了因果态和统计复杂度概念和涌现的量化方法。下面是一些链接能够帮助读者更好的了解因果涌现的相关信息：

因果涌现读书会

• 因果涌现读书会简介

读书会通过阅读前沿文献，加深我们对因果、涌现等概念的理解；聚焦于寻找因果与涌现、多尺度等概念相结合的研究方向；并探索复杂系统多尺度自动建模的研究方向。并探索复杂系统多尺度自动建模的研究方向。分享近期发展起来的一些理论与工具，包括因果涌现理论、机器学习驱动的重整化技术，以及自指动力学正在发展一套跨尺度的分析框架等。

• 因果涌现读书会第二季

涌现与因果的结合创造了因果涌现的概念。这是一套利用因果性来定量刻画涌现的理论体系，本季读书会通过阅读前沿文献，加深我们对因果、涌现等概念的理解；聚焦于寻找因果与涌现、多尺度等概念相结合的研究方向；并探索复杂系统多尺度自动建模的研究方向。第二季读书会更加集中在探讨因果科学与因果涌现之间的关系，以及对涌现进行定量刻画，聚焦于寻找因果与涌现、多尺度等概念相结合的研究方向；并探索复杂系统多尺度自动建模的研究方向。

• 因果涌现读书会第三季

因果涌现第三季的读书会中，将进一步围绕因果涌现的核心研究问题『因果涌现的定义』以及『因果涌现的辨识』来进行深入的学习和讨论，对 Erik Hoel 提出的 Causal Emergence，Causal Geometry 等因果涌现的核心理论进行深入的探讨和剖析，并且详细梳理其中涉及到的方法论，包括从动力学约简、隐空间动力学学习等其他研究领域中学习和借鉴相关的研究思路，最后探讨因果涌现的应用，包括基于生物网络、脑网络或者涌现探测等问题展开扩展，发掘更多的实际应用场景。

路径推荐

• 因果涌现第二季：13.计算力学：模式、预测、结构与简洁性
• 因果涌现第三季：5.计算力学：量化涌现的另一条路径