“计算力学”的版本间的差异
| 第94行: | 第94行: | ||
性质2(因果态具有最小统计复杂度):设<math>\hat{\mathcal{R}} </math>为满足性质1中不等式等号成立的有效态,则对于所有的<math>\hat{\mathcal{R}} </math>,都有<math>C_\mu(\hat{\mathcal{R}})\geq C_\mu(\mathcal{S}) </math>。可以理解为在相同预测能力的前提下,因果态集合<math>\mathcal{S} </math>在有效态集合<math>\mathcal{R} </math>的所有类型中,它的统计复杂度最小,证明过程如下: | 性质2(因果态具有最小统计复杂度):设<math>\hat{\mathcal{R}} </math>为满足性质1中不等式等号成立的有效态,则对于所有的<math>\hat{\mathcal{R}} </math>,都有<math>C_\mu(\hat{\mathcal{R}})\geq C_\mu(\mathcal{S}) </math>。可以理解为在相同预测能力的前提下,因果态集合<math>\mathcal{S} </math>在有效态集合<math>\mathcal{R} </math>的所有类型中,它的统计复杂度最小,证明过程如下: | ||
| − | + | 若<math>H[\stackrel{\rightarrow}{S}^L|\mathcal{R}]= H[\stackrel{\rightarrow}{S}^L|\mathcal{S}] </math>,则存在函数<math>g </math>使得<math>\mathcal{S}=g(\hat{\mathcal{R}}) </math>总是成立。 | |
| − | + | 根据<math>\mathcal{R} </math>的定义可知,<math>H[\vec{S}^L|\mathcal{R}]<LH[S] </math>,则<math>H[f(X)]\leqslant H[X] </math>。 | |
| + | |||
| + | 所以<math>H[S]=H[g(\hat{\mathcal{R}})]\leqslant H[\hat{\mathcal{R}}] </math> | ||
| + | |||
| + | 根据统计复杂度的定义可知,<math>C_\mu(\mathcal{R})\equiv H[\mathcal{R}] </math>,则<math>C_\mu(\hat{\mathcal{R}})=H[\hat{\mathcal{R}}] </math>。 | ||
| + | |||
| + | 所以<math>C_\mu(\hat{\mathcal{R}})\geq C_\mu(\mathcal{S}) </math> | ||
结合本条性质,公式<math>K(s^L )≈C_μ (s^L )+h_μ L </math>中求<math>C_μ (s^L ) </math>就是求<math>s^L </math>对应的因果态的统计复杂度,也就是说想要计算<math>C_μ (s^L ) </math>需要先找到<math>s^L </math>对应的因果态。上式也可以理解为:序列<math>s^L </math>的总信息量≈被归纳的因果态信息量+放弃归纳的随机信息量 | 结合本条性质,公式<math>K(s^L )≈C_μ (s^L )+h_μ L </math>中求<math>C_μ (s^L ) </math>就是求<math>s^L </math>对应的因果态的统计复杂度,也就是说想要计算<math>C_μ (s^L ) </math>需要先找到<math>s^L </math>对应的因果态。上式也可以理解为:序列<math>s^L </math>的总信息量≈被归纳的因果态信息量+放弃归纳的随机信息量 | ||
2024年9月20日 (五) 10:31的版本
计算力学(Computational Mechanics)是一套用于量化涌现的框架。它以一种计算的视角,研究观察者识别涌现时,模型发生的变化。计算力学以信息论和生物进化的思想为基础,是目前最早的对涌现的定量化研究。在应用当中,该理论提出了对复杂性度量的新指标,并有一套实现涌现识别的机器重构算法。
问题背景
自然和社会现象
复杂系统的涌现问题由来已久[1][2][3][4]。鸟群以步调一致地形式飞行。蚁群形成复杂的社会,产生特异化的社会分工。几个世纪前,木星大气中五彩斑斓的混沌运动形成了被称之为“大红斑”的巨大漩涡,至少已存在二百到三百五十年,期间还在不断地改变颜色和形状。
我们直觉中对这样的涌现现象的描述是有新东西冒出来了,比如社会、红斑等等。但是我们没能说明“新东西”是什么,以及它“新”在哪里。所以我们还需要更精确的语言对涌现现象进行识别和描述。
不同层次的涌现
对于一个由很多智能体构成的复杂系统,我们从直觉出发,从模糊到精确,可以划分出对不同层次涌现的定义:
- 对涌现的直觉定义:系统中出现任何可以被称为新颖的特征,即系统有宏观的特征;
- 斑图涌现(Pattern Formation):某一个外在的观察者,用某种编码方式在系统中发现斑图。
- 内在涌现(Intrinsic Emergence):系统本身(构成系统的智能体)捕捉并利用它自身出现的斑图。
下面我们用一些例子来说明对涌现不同层次的描述。
涌现通常被理解为一个过程,该过程导致出现的结构并未直接由控制系统的定义约束和瞬时力描述。随着时间的推移,“新特征”出现在运动方程直接指定的尺度之外。比如一堆随机运动的粒子,虽然瞬时力可以用运动方程描述,但是从宏观尺度上会表现出压强、体积以及温度等新特征。我们需要明确特征是什么以及它新在哪里。否则这一概念几乎没有内容,因为几乎任何时间依赖的系统都会表现出涌现特征。
举两个例子来说明斑图涌现的特征,一个例子是确定性混沌,确定性运动方程随着时间的推移导致了看似不可预测的行为。系统从初始条件映射到后来的状态,变得极为复杂,以至于观察者既无法足够准确地测量系统,也无法以有限的计算资源预测未来的行为。这种混沌的涌现既是非线性动力学系统复杂行为的产物,也是观测者能力的限制。另一个例子是二维的自避免随机游走,粒子的逐步行为由随机方程直接规定:每次移动时,它朝随机方向移动,除非是刚刚离开的方向。经过一段时间,结果是路径描绘出一个自相似的分形结构。在这种情况下,分形结构从大部分随机的逐步运动中涌现出来。
第一个例子的新增特征是不可预测性;第二个例子则是自相似性。在这两种情况下的新颖性都因其涌现特征与系统的定义特征直接对立而加剧:完全的确定性在混沌下隐藏,而几乎完全的随机性下则显现出自相似的有序性。但这些涌现特征对谁而言是“新”的呢?混沌动力学系统的状态在应用确定性函数时总是移动到唯一的下一个状态。显然,系统状态并不知道它的行为是不可预测的。对于随机游走,“分形特征”不在执行局部步骤的粒子“眼中”,这本身就是定义上的,两种情况下的新颖性都在于系统外的观察者眼中。
实际上,检测到的斑图通常是通过观察者选择的统计数据来隐含假定的,可能某些斑图的功能表现与现象的数学模型一致,但这些模型本身依赖于一系列理论假设。简而言之,在斑图形成领域,斑图通常是被猜测出来的,观察者通过固定的规律库预期这些结构,然后再进行验证。类似于通信频道的类比,观察者就像是一个已经手握密码本的接收者。任何未能通过密码本解码的信号本质上都是噪声,即观察者未能识别的斑图。
在系统内部的协调行为中,有一种斑图涌现变得重要,即这些模式在系统的其他结构中显现其“新颖性”。由于没有外部的参照来定义新颖性或斑图,我们可以将这个过程称为内在涌现。在高效资本市场中,竞争性主体根据从集体行为中涌现出的最优定价控制其个人生产-投资和股票所有权策略。对于主体的资源配置决策而言,通过市场的集体行为涌现出的价格是准确的信号,完全反映了所有可用信息,这一点至关重要。内在涌现的独特之处在于形成的斑图赋予了系统额外的功能性,支持全局信息处理,如设定最优价格。这种方法可以直接嵌入系统非线性计算过程之中。更具体地说,假设在内在涌现过程中,内在计算能力的增加可以被利用,从而可以赋予系统额外的功能性。
进化的系统模型
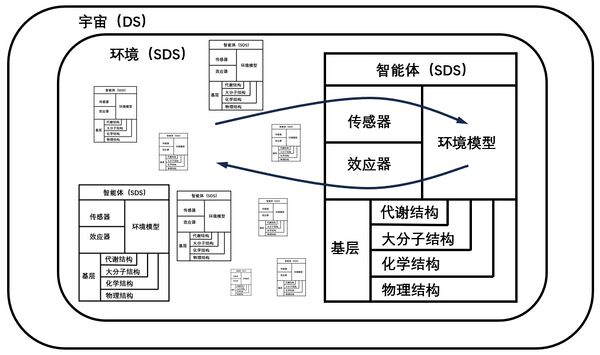
我们可以用生物进化的思想来阐述内在涌现的问题,解释一个高度有序系统是怎么从混沌中涌现的,但是它在解释生命形式的多样性方面预测能力有限。因此要将系统限制在一个结构和生物特征明确的原型宇宙,并把它简化为包括一个环境和一组适应性的观察者或“智能体”。这样才能清晰地定义智能体的性质。智能体(Agent)试图构建和维持一个对其环境具有最大预测能力的内部模型。每个智能体的环境是其他智能体的集合,可以视为一个随机动力系统(Stochastic Dynamical Systems,简称SDS)。在任何给定的时刻,智能体感知到的是当前环境状态的投影。也就是说,环境状态被智能体的感官装置(传感器)所隐藏。随着时间的推移,感官装置产生一系列测量,这些测量引导智能体利用其可用资源(下图的基层)来构建内部环境模型。基于环境模型捕捉到的规律,智能体通过效应器采取行动,最终改变环境状态。如果智能体可以将测量结果尽可能划分随机和确定的部分,然后尽可能捕捉确定的规律,智能体就能利用环境中的更多规律,这种优势会提高智能体的生存能力。
上图为以智能体为中心的环境视图:宇宙可以被视为一个确定性动力系统(Deterministic Dynamical Systems,简称DS),即使规则和初始条件是确定的,随着规模的增长,系统也会变得极为复杂。每个智能体所看到的环境是一个由所有其他智能体组成的随机动力系统(SDS)。其随机性源于其内在的随机性和有限的计算资源。每个智能体本身也是一个随机动力系统,因为它可能会从其基层和环境刺激中采样或受到无法控制的随机性困扰。基层代表支持和限制信息处理、模型构建和决策的可用资源。箭头表示信息流入和流出智能体的方向。
智能体面临的基本问题是基于对隐藏环境状态的建模和对未来环境的预测。这需要一个量化的理论来描述智能体如何处理信息和构建模型。
模型的量化指标
香农熵率
柯式复杂度[math]\displaystyle{ K(x) }[/math]是指在通用确定性图灵机(UTM)上运行时输出的最小程序所需的比特数。不同的程序语言描述同一程序的[math]\displaystyle{ K(x) }[/math]是可以比较的,但也无法确定哪种程序语言有最小的[math]\displaystyle{ K(x) }[/math],同一种程序语言在描述不同程序时[math]\displaystyle{ K(x) }[/math]也并不相同,所以柯式复杂度通常是不可计算的。如果待测对象是由信息源(例如马尔可夫链)生成的离散符号序列[math]\displaystyle{ s^L }[/math] ,[math]\displaystyle{ L }[/math]为序列的长度,其柯式复杂度的香农熵率[math]\displaystyle{ h_μ }[/math]为:
[math]\displaystyle{ \frac{K\left(s^{L}\right)}{L}\underset{L\to\infty}{\operatorname*{\operatorname*{\operatorname*{\rightarrow}}}}h_{\mu} }[/math],转化为公式形式为:[math]\displaystyle{ h_\mu=\lim_{L\to\infty}\frac{H(\Pr(s^L))}L }[/math]
其中[math]\displaystyle{ \Pr(s^L) }[/math]是[math]\displaystyle{ s^L }[/math]的边际分布,[math]\displaystyle{ H }[/math]是自信息的平均值,在建模框架中,[math]\displaystyle{ h_μ }[/math]是信息不确定性程度的归一化指标,信息的不确定性越高,香农熵率越大,在这里可以解释为智能体在预测序列[math]\displaystyle{ s^L }[/math]的后续符号时的误差率。
统计复杂度
粗略地说,柯式复杂度[math]\displaystyle{ K(x) }[/math]需要考虑对象中的所有比特,包括随机比特。其主要后果是[math]\displaystyle{ K(x) }[/math]中数值[math]\displaystyle{ x }[/math]被随机性的生成所主导,因此掩盖了对象以及其生成过程中的重要结构。相比之下,统计复杂度[math]\displaystyle{ C_μ(x) }[/math]剔除了通用图灵机在模拟中随机比特时所花费的计算努力。统计复杂度的一个定义性特征是,对于完全随机对象[math]\displaystyle{ C_μ(x)=0 }[/math],如抛硬币产生的序列,同时对于简单的周期性过程,如[math]\displaystyle{ x=00000000…0 }[/math]时,也有[math]\displaystyle{ C_μ(x)=0 }[/math]。因此,统计复杂度的值对于(简单的)周期性过程和理想随机过程都很小。如果[math]\displaystyle{ s^L }[/math]表示[math]\displaystyle{ x }[/math]的前[math]\displaystyle{ L }[/math]个符号,那么复杂性之间的关系简单地为:
[math]\displaystyle{ K(s^L )≈C_μ (s^L )+h_μ L }[/math]
如果在已确定描述语言(程序)的情况下,柯式复杂度[math]\displaystyle{ K(s^L ) }[/math]可以理解为描述[math]\displaystyle{ s^L }[/math]所用的总信息量。[math]\displaystyle{ h_μ L }[/math]为允许损失的随机信息量。统计复杂度[math]\displaystyle{ C_μ (s^L ) }[/math]可以理解为允许存在误差率[math]\displaystyle{ h_μ }[/math]的情况下,描述[math]\displaystyle{ s^L }[/math]所用的最少信息量。
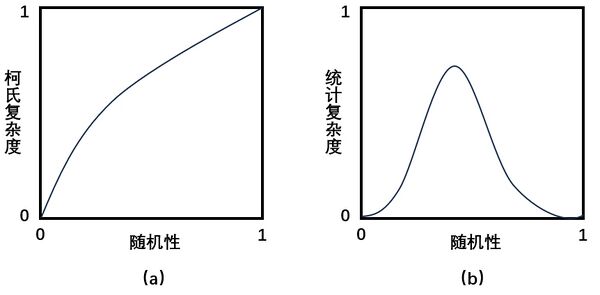
在下图中,展示了柯式复杂度和统计复杂度在从简单周期性到理想随机的过程中的差异。如图(a)所示,确定性复杂性是过程中的理想随机度的单调递增函数,它由过程的香农熵率决定。相反,统计复杂度在两个极端点上均为零,并在中间达到最大值(见图(b))。在中等随机度的“复杂”过程是有序和随机计算元素的组合。组成过程的不可简约组件越多,过程就越“复杂”。
图(a)为柯式复杂度,是对信息源不可预测程度的度量。它表示可以通过香农熵率来衡量的随机性程度。图 (b) 统计复杂统计基于这样的观点:随机性在统计上是简单的:一个理想的随机过程具有零统计复杂度。在另一端,简单的周期性过程具有较低的统计复杂度。复杂过程在这些极端之间产生,并且是可预测机制和随机机制的混合。
因果态
因果态的定义
智能体对环境的测量精度一般都是有限的,测量结果只能描述环境的“隐藏状态”,智能体需要对测量结果粗粒化后才能识别“隐藏状态”中的斑图。若将测量对象过去未来的所有信息视为限制在离散值、离散时间上的稳定随机过程,用双无限序列可数集合[math]\displaystyle{ \overleftrightarrow{S}=⋯s_{-2} s_{-1} s_0 s_1 s_2… }[/math]表示,则测量结果为[math]\displaystyle{ \overleftrightarrow{S} }[/math]中任意随机变量的序列。基于时间[math]\displaystyle{ t }[/math]可以将[math]\displaystyle{ \overleftrightarrow{S} }[/math]分为单侧前向序列[math]\displaystyle{ s_t^→=s_t s_{t+1} s_{t+2} s_{t+3}… }[/math]和单侧后向序列[math]\displaystyle{ s_t^←=⋯s_{t-3} s_{t-2} s_{t-1} }[/math]两个部分,所有可能的未来序列[math]\displaystyle{ s_t^→ }[/math]形成的集合记作[math]\displaystyle{ \overrightarrow{S} }[/math],所有可能的历史序列[math]\displaystyle{ \overleftarrow{s_t} }[/math]形成的集合记作[math]\displaystyle{ \overleftarrow{S} }[/math]。
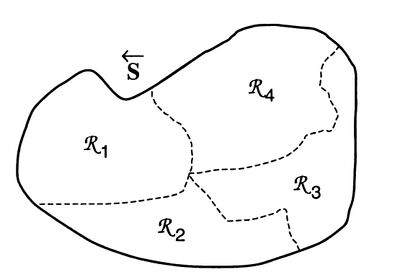
按照一定的划分方法( partition)将[math]\displaystyle{ \overset{\leftarrow}{S} }[/math]划分为若干个互斥且全面的子集,那么每个子集就是一个有效态(effective state),这些有效态的集合记作[math]\displaystyle{ \mathcal{R} }[/math],划分方法可以是任意函数映射[math]\displaystyle{ η }[/math],用公式表示为[math]\displaystyle{ \eta{:}\overleftarrow{S}\mapsto\mathcal{R} }[/math],也可以将有效态理解为将[math]\displaystyle{ \overset{\leftarrow}{S} }[/math]中的某段序列粗粒化后得到的宏观态。
上图为某种划分方法的示意图,将集合[math]\displaystyle{ \overset{\leftarrow}{S} }[/math]划分为某类有效态[math]\displaystyle{ \mathcal{R}=\{\mathcal{R}_i:i=1,2,3,4\} }[/math],值得注意的是,[math]\displaystyle{ \mathcal{R}_i }[/math]不必形成紧致集,也可以是康托集或其他更特殊的结构,上图为了示意清楚才这样画的。
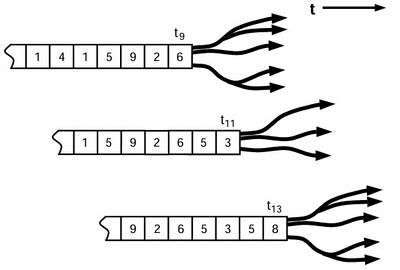
用来划分集合[math]\displaystyle{ \overset{\leftarrow}{S} }[/math]的映射可以有很多种,若某一种划分方法能够在预测能力最强的同时消耗的计算资源最少,那么它肯定是最优的划分。为了找到这种最优的划分,需要定义因果态的概念,因果态就是智能体对测量结果进行处理后,根据其内部模型(尤其是状态结构)识别出的斑图,并且这种斑图不随时间发生变化。形式化定义为:对于任意的时间点[math]\displaystyle{ t }[/math] 和[math]\displaystyle{ t^{'} }[/math],给定过去状态[math]\displaystyle{ s_t^← }[/math]的条件下,未来状态[math]\displaystyle{ s^→ }[/math]的分布与给定过去状态[math]\displaystyle{ s_{t^{'}}^← }[/math]的条件下,未来状态[math]\displaystyle{ s^→ }[/math]的分布相同。那么[math]\displaystyle{ t }[/math] 和[math]\displaystyle{ t^{'} }[/math]的关系就记作[math]\displaystyle{ t∼t^{'} }[/math],“[math]\displaystyle{ ∼ }[/math] ” 表示由等效未来状态所引起的等价关系,可以用公式表示为:[math]\displaystyle{ t∼t^{'} \triangleq Pr(s^→ |s_t^← )=Pr(s^→ |s_{t^{'}}^← ) }[/math],若[math]\displaystyle{ t }[/math] 和[math]\displaystyle{ t^{'} }[/math]对未来状态预测的分布相同,则定义他们具有相同的因果态(casual state)。
如上图所示,在[math]\displaystyle{ t_9 }[/math]和[math]\displaystyle{ t_{13} }[/math]时刻分别对应一个状态,这两个状态处于相同的因果态,因为对未来的预测具有相同的分布;在[math]\displaystyle{ t_{11} }[/math]时刻的状态,则与[math]\displaystyle{ t_9 }[/math]和[math]\displaystyle{ t_{13} }[/math]时刻处于不同的因果态。
因果态的主要性质
因果态是一种特殊的划分方法,它的划分函数记作[math]\displaystyle{ \epsilon }[/math],公式为[math]\displaystyle{ \epsilon{:}\overleftarrow{S}\mapsto2^{\overset{\leftarrow}{S}} }[/math],其中[math]\displaystyle{ 2^{\overset{\leftarrow}{S}} }[/math]是[math]\displaystyle{ \overleftarrow{S} }[/math]的幂集。根据因果态的定义,则存在如下关系:[math]\displaystyle{ \epsilon(\stackrel{\leftarrow}{s})\equiv\{\stackrel{\leftarrow}{s}^{\prime}|\mathrm{P}(\stackrel{\rightarrow}{S}=\stackrel{\rightarrow}{s}\mid\stackrel{\leftarrow}{S}=\stackrel{\leftarrow}{s})=\mathrm{P}(\stackrel{\rightarrow}{S}=\stackrel{\rightarrow}{s}\mid\stackrel{\leftarrow}{S}=\stackrel{\leftarrow}{s}^{\prime}),\mathrm{for~all~}\overrightarrow{s}\in\overrightarrow{S},\stackrel{\leftarrow}{s}^{\prime}\in\stackrel{\leftarrow}{S}\} }[/math],其中[math]\displaystyle{ \mathcal{S} }[/math]为因果态的集合,[math]\displaystyle{ \stackrel{\leftarrow}{s} }[/math]为历史序列的随机变量,[math]\displaystyle{ \mathcal{S} }[/math]是[math]\displaystyle{ \mathcal{R} }[/math]的一种最优形式,因为[math]\displaystyle{ \mathcal{S} }[/math]的如下性质。
性质1(因果态具有最大预测性):对于所有有效态[math]\displaystyle{ \mathcal{R} }[/math]和正整数[math]\displaystyle{ L }[/math],都有[math]\displaystyle{ H[\stackrel{\rightarrow}{S}^L|\mathcal{R}]\geq H[\stackrel{\rightarrow}{S}^L|\mathcal{S}] }[/math],[math]\displaystyle{ \stackrel{\rightarrow}{S}^L }[/math]为[math]\displaystyle{ L }[/math]个长度的未来序列集合,[math]\displaystyle{ H[\stackrel{\rightarrow}{S}^L|\mathcal{R}] }[/math]和[math]\displaystyle{ H[\stackrel{\rightarrow}{S}^L|\mathcal{S}] }[/math]是[math]\displaystyle{ \stackrel{\rightarrow}{S}^L }[/math]的条件熵。可以理解为因果态集合[math]\displaystyle{ \mathcal{S} }[/math]在有效态集合[math]\displaystyle{ \mathcal{R} }[/math]的所有类型中,它的预测能力最强,证明过程如下:
[math]\displaystyle{ \epsilon(\stackrel{\leftarrow}{s})\equiv\{\stackrel{\leftarrow}{s}^{\prime}|\mathrm{P}(\stackrel{\rightarrow}{S}=\stackrel{\rightarrow}{s}\mid\stackrel{\leftarrow}{S}=\stackrel{\leftarrow}{s})=\mathrm{P}(\stackrel{\rightarrow}{S}=\stackrel{\rightarrow}{s}\mid\stackrel{\leftarrow}{S}=\stackrel{\leftarrow}{s}^{\prime}) }[/math]
[math]\displaystyle{ \mathrm{P}(\stackrel{\rightarrow}{S}=\stackrel{\rightarrow}{s} |\mathcal{S}=\epsilon(\stackrel{\leftarrow}{s}))=\mathrm{P}(\stackrel{\rightarrow}{S}=\stackrel{\rightarrow}{s}\mid\stackrel{\leftarrow}{S}=\stackrel{\leftarrow}{s}) }[/math]
[math]\displaystyle{ H[\stackrel{\rightarrow}{S}^L|\mathcal{S}]~=~H[\stackrel{\rightarrow}{S}^L|~\stackrel{\leftarrow}{S}] }[/math]
[math]\displaystyle{ H[\stackrel{\to}{S}^L|\mathcal{R}] \geq H[\stackrel{\to}{S}^L|\stackrel{\leftarrow}{S}] }[/math]
[math]\displaystyle{ H[\stackrel{\rightarrow}{S}^L|\mathcal{R}]\geq H[\stackrel{\rightarrow}{S}^L|\mathcal{S}] }[/math]
性质2(因果态具有最小统计复杂度):设[math]\displaystyle{ \hat{\mathcal{R}} }[/math]为满足性质1中不等式等号成立的有效态,则对于所有的[math]\displaystyle{ \hat{\mathcal{R}} }[/math],都有[math]\displaystyle{ C_\mu(\hat{\mathcal{R}})\geq C_\mu(\mathcal{S}) }[/math]。可以理解为在相同预测能力的前提下,因果态集合[math]\displaystyle{ \mathcal{S} }[/math]在有效态集合[math]\displaystyle{ \mathcal{R} }[/math]的所有类型中,它的统计复杂度最小,证明过程如下:
若[math]\displaystyle{ H[\stackrel{\rightarrow}{S}^L|\mathcal{R}]= H[\stackrel{\rightarrow}{S}^L|\mathcal{S}] }[/math],则存在函数[math]\displaystyle{ g }[/math]使得[math]\displaystyle{ \mathcal{S}=g(\hat{\mathcal{R}}) }[/math]总是成立。
根据[math]\displaystyle{ \mathcal{R} }[/math]的定义可知,[math]\displaystyle{ H[\vec{S}^L|\mathcal{R}]\lt LH[S] }[/math],则[math]\displaystyle{ H[f(X)]\leqslant H[X] }[/math]。
所以[math]\displaystyle{ H[S]=H[g(\hat{\mathcal{R}})]\leqslant H[\hat{\mathcal{R}}] }[/math]
根据统计复杂度的定义可知,[math]\displaystyle{ C_\mu(\mathcal{R})\equiv H[\mathcal{R}] }[/math],则[math]\displaystyle{ C_\mu(\hat{\mathcal{R}})=H[\hat{\mathcal{R}}] }[/math]。
所以[math]\displaystyle{ C_\mu(\hat{\mathcal{R}})\geq C_\mu(\mathcal{S}) }[/math]
结合本条性质,公式[math]\displaystyle{ K(s^L )≈C_μ (s^L )+h_μ L }[/math]中求[math]\displaystyle{ C_μ (s^L ) }[/math]就是求[math]\displaystyle{ s^L }[/math]对应的因果态的统计复杂度,也就是说想要计算[math]\displaystyle{ C_μ (s^L ) }[/math]需要先找到[math]\displaystyle{ s^L }[/math]对应的因果态。上式也可以理解为:序列[math]\displaystyle{ s^L }[/math]的总信息量≈被归纳的因果态信息量+放弃归纳的随机信息量
性质3(因果态具有最小随机性):设[math]\displaystyle{ \hat{\mathcal{R}} }[/math]和[math]\displaystyle{ \hat{\mathcal{R}}^{\prime} }[/math]为满足性质1中不等式等号成立的有效态,则对于所有的[math]\displaystyle{ \hat{\mathcal{R}} }[/math]和[math]\displaystyle{ \hat{\mathcal{R}}^{\prime} }[/math],都有[math]\displaystyle{ H[\hat{\mathcal{R}}^{\prime}|\hat{\mathcal{R}}]\geq H[\mathcal{S}^{\prime}|\mathcal{S}] }[/math],其中[math]\displaystyle{ \hat{\mathcal{R}}^{\prime} }[/math]和[math]\displaystyle{ \mathcal{S}^{\prime} }[/math]分别是该过程的下一时刻有效态和下一时刻因果态。可以理解为在相同预测能力的前提下,因果态集合[math]\displaystyle{ \mathcal{S} }[/math]在有效态集合[math]\displaystyle{ \mathcal{R} }[/math]的所有类型中,它的随机性最小。
用互信息的角度去理解的话,上式等价于[math]\displaystyle{ I(\mathcal{S}^{\prime};\mathcal{S})\geq I(\hat{\mathcal{R}}^{\prime};\hat{\mathcal{R}}) }[/math],可以理解为任意有效态对它自己下一时刻的互信息中,其中因果态的互信息最大,若不考虑Do干预,因果态和因果涌现理论中最大化有效信息所得到的宏观态意义相同。
若想更深入的理解因果态的性质可以阅读James Crutchfield的两篇论文[1][5],里面有因果态更多的性质和对应的形式化证明过程。
斑图重构机器
智能体如何处理测量结果才能识别其中因果态呢?为了解决这个问题,计算力学建立了名为斑图重构机器(ϵ-machine)的模型,它可以重构测量结果中的序列,去除随机噪音后识别其中的因果态。斑图重构机器的大小可以用统计复杂度衡量,它的形式化定义可以用公式表示为[math]\displaystyle{ M=(\mathcal{S},T) }[/math],其中[math]\displaystyle{ T }[/math]为状态到状态映射的集合,满足[math]\displaystyle{ S_{t+1}=TS_t }[/math],[math]\displaystyle{ S }[/math]为集合[math]\displaystyle{ \mathcal{S} }[/math]中的任意一个因果态,它类似于一个粗粒化后的宏观动力学。[math]\displaystyle{ T_{ij}^{\left ( s \right )} }[/math]为两个因果态[math]\displaystyle{ S_i }[/math]和[math]\displaystyle{ S_j }[/math]之间的因果态转移概率映射,[math]\displaystyle{ T_{ij}^{(s)}\equiv\mathrm{P}(\mathcal{S}'=\mathcal{S}_j,\stackrel{\to}{S}^1=s|\mathcal{S}=\mathcal{S}_i) }[/math]。每个[math]\displaystyle{ \mathcal{S} }[/math]都有[math]\displaystyle{ \epsilon }[/math]函数和[math]\displaystyle{ T }[/math]函数,这两个函数可以组成一个有序对[math]\displaystyle{ \left \{ \epsilon,T \right \} }[/math],通过学习[math]\displaystyle{ \epsilon }[/math]和[math]\displaystyle{ T }[/math]函数可以提高机器识别因果态的准确度。
如果将模型构建视为一个动态过程,那么在模型构建和完善过程中,它的两个量化指标香农熵率[math]\displaystyle{ h_μ }[/math]和统计复杂度[math]\displaystyle{ C_μ }[/math]可以分别用来监测智能体模型的预测能力和模型大小。由于外部环境实际熵率与智能体内部模型的熵率之间的绝对差异决定了智能体的预测误差率,因此模型的熵率越接近外部环境的熵率,智能体的生存机会就越高。但这种生存能力是有代价的,这个代价由智能体在进行预测时必须投入的计算资源决定的,这种代价的量度就是模型的统计复杂度。
模型的创新与重构
模型创新
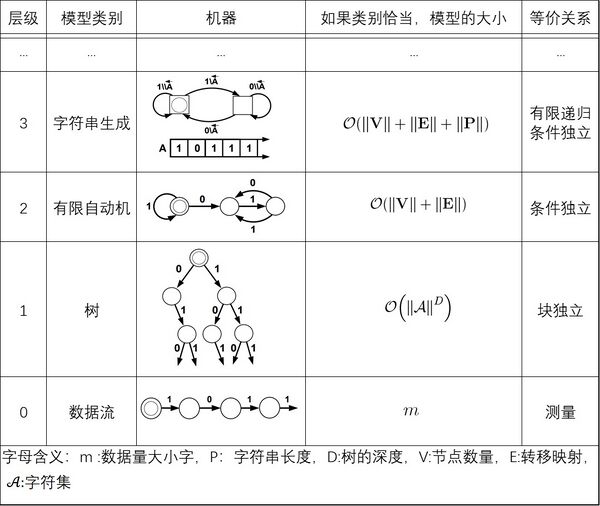
由于智能体的计算资源有限,若测量结果中的数据量超过模型的处理极限时,就需要对原有模型进行创新以保障在计算资源不变的情况下智能体对外界的有效预测,创新方法主要是通过寻找原有模型状态组之间的相似性,在原有模型识别到的因果态中抽象出更高层级的因果态组。下表中列举了一种模型创新的途径:
上表为因果时间序列建模层级,展示了可能的前四个层级,但这个过程是开放式的,可以不止四个层级,每个层级根据其模型类别定义。模型本身由状态(圆圈或方块)和转移(标记箭头)组成,每个模型都有一个独特的起始状态,由一个内嵌的圆圈表示。数据流本身是最低层级,通过将序列测量分组为重复子序列,从数据流中构建出深度为的树。下一个层级的模型,即具有状态和转移的有限自动机(FA),通过将树节点分组从树中重构。所示的最后一个层级,字符串生成机器(PM),通过将FA状态分组并推断出操控寄存器A中字符串的生成规则来构建。
考虑一个由[math]\displaystyle{ m }[/math]个测量结果构成的数据流[math]\displaystyle{ s }[/math],如果它是周期性的,那么第0级(Level 0),即测量结果本身,它的表示方法依赖于[math]\displaystyle{ m }[/math]。在极限[math]\displaystyle{ m\to\infty }[/math]情况下,第0级会产生一个无穷大的表示。当然,第0级是最准确的数据模型,尽管它几乎没有任何帮助,几乎不值得被称为“模型”。相比之下,一个深度为[math]\displaystyle{ D }[/math]的树将给出一个有限表示,即使数据流的长度是无限的,只要数据流具有周期小于等于[math]\displaystyle{ D }[/math]。这个树有长度为[math]\displaystyle{ D }[/math]的路径,由数据流的周期给出。这些路径中的每一个都对应于[math]\displaystyle{ s }[/math]中重复模式的一个不同阶段。如果[math]\displaystyle{ s }[/math]是非周期性的,那么树模型类将不再是有限的,并且与[math]\displaystyle{ m }[/math]无关。 事实上,如果数据流具有正熵([math]\displaystyle{ h_μ>0 }[/math]),那么树的大小将呈指数增长,[math]\displaystyle{ \approx\left\|\mathcal{A}\right\|^{Dh_{\mu}} }[/math] ,因为[math]\displaystyle{ D }[/math]的增加解释了[math]\displaystyle{ s }[/math] 中长度[math]\displaystyle{ D }[/math]不断增加的子序列。粗略地说,如果数据流具有随时间衰减得足够快的相关性,则下一级(随机)有限自动机将给出有限表示。状态数[math]\displaystyle{ \left\|\mathrm{V}\right\| }[/math]表示数据流中的内存量,因此表示[math]\displaystyle{ s }[/math]中测量值之间存在相关性的典型时间。但也有可能第 2 级不提供有限表示。那么就需要另一个级别(第 3 级)。
模型重构算法
上面介绍了斑图重构机器,是智能体识别因果态的一种方式。若结合模型创新的概念,就可以给出斑图重构机器的完整定义:斑图重构机器(ϵ-machine)是能够用最少的计算资源对测量结果进行有限描述同时复杂度最小的模型。模型的算法步骤如下:
1. 在最低水平上,设定0级模型为描述数据本身,即[math]\displaystyle{ M_0=s }[/math],将初始层级[math]\displaystyle{ l }[/math]设置为比0级高一级,即[math]\displaystyle{ l=1 }[/math];
2. 从更低模型重构模型[math]\displaystyle{ M_l=M_{l-1}/∼ }[/math],其中[math]\displaystyle{ ∼ }[/math]表示[math]\displaystyle{ l }[/math]级上的因果等价类;操作的含义是,在[math]\displaystyle{ l-1 }[/math]级上被区别对待的状态在[math]\displaystyle{ l }[/math]级上可以被视为同一个因果态。此时[math]\displaystyle{ \mathcal{S} }[/math]和[math]\displaystyle{ T }[/math]都更新了;
3. 收集更多的数据,增大序列长度[math]\displaystyle{ L }[/math],得到更加精确的一系列模型[math]\displaystyle{ M_l }[/math];
4. 如果随着[math]\displaystyle{ L }[/math]增大,模型的复杂度发散,即[math]\displaystyle{ C_μ(M_l) = \lVert M_l \rVert \underset{ϵ \to 0}{\to} \infty }[/math],那么回到第二步,得到更高级模型[math]\displaystyle{ M_{l+1} }[/math];
5. 如果模型复杂度收敛,意味着重建好了一个合适的模式重构机器,程序退出。
混沌动力学实例
逻辑斯谛映射
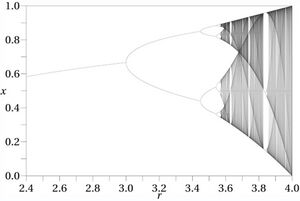
接下来将采用具体的方法来演示如何将计算力学的理论应用于实际案例[2],要演示的是混沌动力学中的逻辑斯谛映射(logistic map),特别是其周期倍增的混沌路径。用于重建模型的数据流来自逻辑斯谛映射的轨迹,轨迹是通过迭代映射[math]\displaystyle{ x_{n+1}=f(x_n) }[/math]生成的,迭代函数为[math]\displaystyle{ f(x) = rx(1-x) }[/math],其中非线性参数[math]\displaystyle{ \begin{matrix}r&\in&[0,4]\end{matrix} }[/math],初始条件[math]\displaystyle{ x_0\in[0,1] }[/math],迭代函数的最大值出现在[math]\displaystyle{ x_c = \frac12 }[/math]。
上图为迭代函数[math]\displaystyle{ f(x) = rx(1-x) }[/math]中[math]\displaystyle{ r }[/math]与[math]\displaystyle{ x }[/math]的关系图,当[math]\displaystyle{ r<3.5699... }[/math]时函数存在倍周期现象,当[math]\displaystyle{ r>3.5699... }[/math]时会出现混沌现象。若要识别混沌中的有序结构,就需要对[math]\displaystyle{ x }[/math]进行粗粒化操作,方法是通过二元分割观察轨迹[math]\displaystyle{ \mathbf{x}=x_0x_1x_2x_3\ldots }[/math] ,将其转换为离散序列[math]\displaystyle{ \mathcal{P}=\{x_n\in[0,x_c)\Rightarrow s=0,x_n\in[x_c,1]\Rightarrow s=1\} }[/math],这种划分是“生成”的,这意味着足够长的二进制序列来自任意小的初始条件间隔。因此,可以使用粗粒化的观测[math]\displaystyle{ \mathcal{P} }[/math]来研究逻辑斯谛映射中的信息处理。
统计复杂度-熵率图
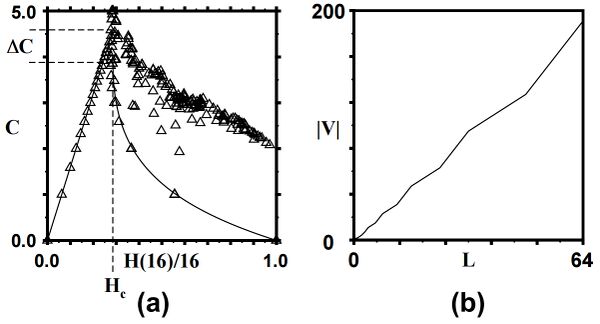
上图(a)为逻辑斯谛映射中统计复杂度[math]\displaystyle{ C_μ }[/math]与香农熵率[math]\displaystyle{ H(L)/L }[/math]的关系,三角形表示[math]\displaystyle{ (C_μ ,H(L)/L) }[/math]的大概位置,对应非线性参数[math]\displaystyle{ r }[/math]的 193 个取值,其中子序列长度[math]\displaystyle{ L=16 }[/math],覆盖部分实验数据的粗实线是[math]\displaystyle{ C_μ =0 }[/math]时对[math]\displaystyle{ H(L)/L }[/math]得出的分析曲线。本图表现两个重要特征。第一个特征是熵的极值导致零复杂度,也就是说在[math]\displaystyle{ H(L)/L=0 }[/math]处最简单的周期过程和在[math]\displaystyle{ H(L)/L=1 }[/math]处最随机的过程在统计上都是简单的,它们都具有零复杂度,因为它们是由具有单一状态的斑图重构机器描述的。第二个特征是在两个极端情况之间,过程明显更为复杂,在临界熵值[math]\displaystyle{ H_c }[/math]附近出现明显峰值(此处[math]\displaystyle{ r=3.5699... }[/math]),[math]\displaystyle{ H(L)/L }[/math]小于[math]\displaystyle{ H_c }[/math]时数据集在呈周期性(包括在混沌区域也呈周期性的参数)的参数下产生,大于[math]\displaystyle{ H_c }[/math]时数据集在混沌的参数下产生。本图可以对照统计复杂度小节中的图(b)理解。
上图(b)为逻辑斯谛映射中在[math]\displaystyle{ r=3.5699... }[/math]处,[math]\displaystyle{ L }[/math]与隐状态数量[math]\displaystyle{ \left|\mathbf{V}\right| }[/math]的关系,序列的长度[math]\displaystyle{ L=64 }[/math]时,[math]\displaystyle{ \left|\mathbf{V}\right|=196 }[/math],从图中可以看出,随着[math]\displaystyle{ L }[/math]的增长,[math]\displaystyle{ \left|\mathbf{V}\right| }[/math]的值是发散的,若要用有限的[math]\displaystyle{ L }[/math]来描述[math]\displaystyle{ \left|\mathbf{V}\right| }[/math],就需要将模型进行创新升级为描述能力更强的模型。
模型升级
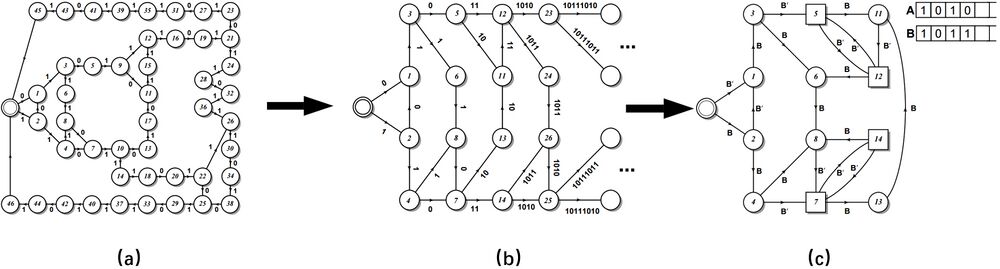
上图(a)为逻辑斯谛映射在[math]\displaystyle{ r=3.5699... }[/math]处混沌首次出现的倍周期轨迹的近似值,且序列长度[math]\displaystyle{ L=16 }[/math]时用斑图重构机器重构后的47个状态路径图。它捕捉到的规律并不明显,我们将它进行一个简单的转换,用相应的序列替换机器中未分支的路径后就是图(b),图(b)中的分支状态相当有规律,更进一步将图(b)升级为用字符生成器来描述机器增长的规律性,如图(c)所示,有限自动机有两种状态(原有类型用圆圈表示,新类型用方块表示)和两个寄存器 A 和 B,A 和 B用于保存二进制字符串,初始状态 A 中保存的是0,B中保存的是1,B'表示对保存在B中的字符串的最后一位取反。观察一下图(b)就会发现字符串操作可以通过将 A 的内容副本附加到 B 上,并用 B 的内容的两个副本替换 A 的内容来描述。这些字符串在方块处迭代,迭代式表示为 A→BB 和 B→BA。显然(c)的方式比(a)的方式更加节省计算资源,它的描述能力也更强。
参考文献
- ↑ 1.0 1.1 James P. Crutchfield, Karl Young. Inferring Statistical Complexity. PHYSICAL REVIEW LETTERS, VOLUME 63, NUMBER 2. 10 JULY 1989
- ↑ 2.0 2.1 James P. Crutchfield. The Calculi of Emergence: Computation, Dynamics, and Induction. SFI 94-03-016. 1994
- ↑ James E. Hanson, James P. Crutchfield. Computational Mechanics of Cellular Automata: An Example. SFI WORKING PAPER: 1995-10-095
- ↑ Cosma Rohilla Shalizi, James P. Crutchfield. Computational Mechanics: Pattern and Prediction, Structure and Simplicity. February 1, 2008
- ↑ Shalizi, C. R.. & Crutchfield, J. P. (2001). Computational Mechanics: Pattern and Prediction, Structure and Simplicity,Journal of Statistical Physics,104(3/4).817-879.
编者推荐
计算力学和因果涌现关系密切,计算力学的很多概念与因果涌现相似,只是描述方式不同。下面是一些链接能够帮助读者更好的了解因果涌现的相关信息:
因果涌现读书会
读书会通过阅读前沿文献,加深我们对因果、涌现等概念的理解;聚焦于寻找因果与涌现、多尺度等概念相结合的研究方向;并探索复杂系统多尺度自动建模的研究方向。并探索复杂系统多尺度自动建模的研究方向。分享近期发展起来的一些理论与工具,包括因果涌现理论、机器学习驱动的重整化技术,以及自指动力学正在发展一套跨尺度的分析框架等。
涌现与因果的结合创造了因果涌现的概念。这是一套利用因果性来定量刻画涌现的理论体系,本季读书会通过阅读前沿文献,加深我们对因果、涌现等概念的理解;聚焦于寻找因果与涌现、多尺度等概念相结合的研究方向;并探索复杂系统多尺度自动建模的研究方向。第二季读书会更加集中在探讨因果科学与因果涌现之间的关系,以及对涌现进行定量刻画,聚焦于寻找因果与涌现、多尺度等概念相结合的研究方向;并探索复杂系统多尺度自动建模的研究方向。
因果涌现第三季的读书会中,将进一步围绕因果涌现的核心研究问题『因果涌现的定义』以及『因果涌现的辨识』来进行深入的学习和讨论,对 Erik Hoel 提出的 Causal Emergence,Causal Geometry 等因果涌现的核心理论进行深入的探讨和剖析,并且详细梳理其中涉及到的方法论,包括从动力学约简、隐空间动力学学习等其他研究领域中学习和借鉴相关的研究思路,最后探讨因果涌现的应用,包括基于生物网络、脑网络或者涌现探测等问题展开扩展,发掘更多的实际应用场景。