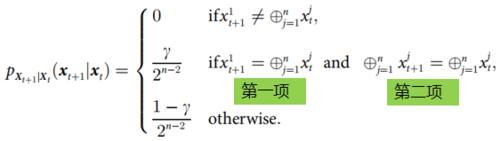因果涌现
因果涌现(causal emergence)是指动力系统中的一类特殊的涌现现象,即系统在宏观尺度会展现出更强的因果特性。特别的,对于一类马尔科夫动力系统来说,在对其状态空间进行适当的粗粒化以后,所形成的宏观动力学会展现出比微观更强的因果特性,那么称该系统发生了因果涌现[1][2]。
历史
相关概念的发展
因果涌现理论是一种试图用基于因果的定量研究方法回答什么是涌现这一重要问题的,因此因果涌现的发展与人们对涌现和因果等概念的认识和发展密切相关。
涌现
涌现一直是复杂系统中的一个重要特性和研究对象,是许多关于复杂性本质以及宏微观组织之间关系讨论的核心概念[3][4]。涌现可以简单理解为整体大于部分之和,即整体上展现出构成它的个体所不具备的新特性[5]。尽管学者们在各个领域都指出存在涌现的现象[4][6],如鸟类的群体行为[7],大脑中的意识形成,以及大语言模型的涌现能力[8],但目前还没有对这一现象的被普遍认可的统一理解。以往对涌现有很多定性的研究,如 Bedau et al[9][10]对涌现进行了分类,可以将涌现分为名义涌现[11][12]、弱涌现[9][13]与强涌现[14][15]。名义涌现可以理解为能被宏观层级的模式或过程所拥有,但不能被其微观层级的组件所拥有的属性[11][12]。弱涌现是指宏观层面的属性或过程是通过单个组件之间以复杂的方式相互作用产生的,由于计算不可约性的原理,它们不能轻易地简化为微观层面的属性。对于弱涌现来说,其模式产生的原因可能来自微观和宏观两个层面[14][15]。因此,涌现的因果关系可能与微观因果关系并存。而对于强涌现来说存在很多的争论,它指的是宏观层面的属性,原则上不能简化为微观层面的属性,包括个体之间的相互作用。此外,Jochen Fromm进一步将强涌现解释为向下因果的因果效应[16]。考虑一个包含三个不同尺度的系统:微观、介观和宏观。向下因果关系是指从宏观层面向介观层面或从介观层面向微观层面的因果力。然而,关于向下因果关系本身的概念存在许多争议[17][18]。
由这些早期研究可以看出,涌现与因果有着天然的深刻联系。
因果及其度量
所谓的因果就是指事件彼此之间的相互影响。因果不等于相关,这体现为,不仅当A发生时B会发生,而且如果A不发生,则B必然不发生。人们只有通过干预事件A,从而考察B的结果,才能探测A与B是否存在着因果关系。
随着近年来因果科学得到了进一步的发展,使得人们可以用数学框架来量化因果,因果描述的是一个动力学过程的因果效应[19][20][21]。Judea Pearl[21]利用概率图模型来描述因果相互作用。Pearl用不同的模型来区分并量化了三个层次的因果关系,这里我们比较关注因果阶梯中的第二层:对输入分布做干预。此外,由于发现的因果关系背后的不确定性和模糊性,测量两个变量之间的因果效应程度是另一个重要问题。许多独立的历史研究已经解决了因果关系测量的问题。这些测量方法包括休谟的恒定连接概念[22]和基于值函数的方法[23],Eells和Suppes将概率的提高作为因果关系的度量[24][25],以及Judea Pearl的因果度量等[19]。
因果涌现
涌现和因果也是相互联系的:一方面,涌现是复杂系统中各组成部分之间复杂的非线性相互作用的因果效应;另一方面,涌现特性也会对复杂系统中的个体产生因果关系。此外,以往会把很多东西归结为一些微观因素,但是宏观涌现出来的模式,往往无法归因到微观层面并进行解释,所以也就无法找到对应的原因。同时虽然有了涌现的定性分类,然而却无法定量的刻画涌现的发生。因此,可以借助因果来定量刻画涌现的发生。2013美国理论神经生物学家Erik Hoel尝试将因果引入涌现的衡量,提出了因果涌现这一概念,并且使用有效信息(Effective Information,简称EI)来量化系统动力学的因果性强弱[1][2]。因果涌现可以描述为:当一个系统在宏观尺度相较其在微观尺度上具有更强的因果效应,此即产生了因果涌现。因果涌现很好的刻画了系统宏观和微观状态之间的区别与联系,同时把人工智能中的因果和复杂系统中的涌现这两个核心概念结合起来,因果涌现也为学者回答一系列的哲学问题提供了一个定量化的视角。比如,可以借助因果涌现框架讨论生命系统或者社会系统中的自上而下的因果等特性。这里的自上而下因果指的是向下因果[26],表示存在宏观到微观的因果效应。例如,壁虎断尾现象,当遇到危险时壁虎不征求尾巴的建议直接将自己的尾巴断掉,这里整体是因,尾巴是果,那么就存在一个整体指向部分的因果力。
早期相关工作
早期已经有一些相关的工作尝试对涌现进行定量的分析。Crutchfield等[27]提出的计算力学理论考虑了因果态,该方法是在状态空间划分的基础上展开相关概念的讨论的,与Erik Hoel的因果涌现理论存在着很大的相似性。而Seth等人则提出了G-emergence理论[28]利用格兰杰因果关系来量化涌现。
计算力学
计算力学理论试图用定量的框架来表述涌现的因果关系,从一个随机过程的观察中构造一个最小的因果模型,这个模型可以产生观察到的时间序列[27]。其中随机过程可以用[math]\displaystyle{ \overleftrightarrow{s} }[/math]表示,基于时间[math]\displaystyle{ t }[/math]可以将随机过程分为两个部分,时间t前和时间t后的过程,[math]\displaystyle{ \overleftarrow{s_t} }[/math]和[math]\displaystyle{ \overrightarrow{s_t} }[/math],当这个过程是平稳过程时,可以去掉时间。因此,可以将所有可能的历史过程[math]\displaystyle{ \overleftarrow{s_t} }[/math]形成的集合记作[math]\displaystyle{ \overleftarrow{S} }[/math],所有未来的过程形成的集合记作[math]\displaystyle{ \overrightarrow{S} }[/math]。定义一个划分函数[math]\displaystyle{ \eta: \overleftarrow{S}→\mathcal{R} }[/math],可以将[math]\displaystyle{ \overleftarrow{S} }[/math]划分为相互排斥的子集(所有的互斥子集形成全集),形成的集合记为[math]\displaystyle{ \mathcal{R} }[/math],[math]\displaystyle{ R \in \mathcal{R} }[/math]中的任意子集可以看作是一个状态。对于一组状态集合[math]\displaystyle{ \mathcal{R} }[/math],我们使用香农熵定义其统计复杂性指标[math]\displaystyle{ C_\mu }[/math]来衡量其简单性,其中[math]\displaystyle{ C_\mu(\mathcal{R})\triangleq -\sum_{\rho\in \mathcal{R}} P(\mathcal{R}=\rho)\log_2 P(\mathcal{R}=\rho) }[/math],当使用一组状态构建预测模型时,统计复杂性指的是模型的大小。此外,为了使状态集在预见性和简约性之间取得最佳平衡,我们定义了因果等价的概念,如果[math]\displaystyle{ P\left ( \overrightarrow{s}|\overleftarrow{s}\right )=P\left ( \overrightarrow{s}|{\overleftarrow{s}}'\right ) }[/math],则[math]\displaystyle{ \overleftarrow{s} }[/math]和[math]\displaystyle{ {\overleftarrow{s}}' }[/math]是因果等价的,这种等价关系可以将所有的历史过程划分为等价的类,并将它们定义为因果态。将历史过程[math]\displaystyle{ \overleftarrow{s} }[/math]的所有因果态定义为[math]\displaystyle{ \epsilon \left ( \overleftarrow{s} \right ) }[/math],[math]\displaystyle{ \epsilon: \overleftarrow{\mathcal{S}}\rightarrow 2^{\overleftarrow{\mathcal{S}}} }[/math]是一个函数,将历史过程[math]\displaystyle{ \overleftarrow{s} }[/math]映射成因果态[math]\displaystyle{ \epsilon(\overleftarrow{s})\in 2^{\overleftarrow{\mathcal{S}}} }[/math]。将两个因果态[math]\displaystyle{ S_i }[/math]和[math]\displaystyle{ S_j }[/math]之间的因果转移概率记为[math]\displaystyle{ T_{ij}^{\left ( s \right )} }[/math],一个随机过程的[math]\displaystyle{ \epsilon-machine }[/math]被定义为有序对[math]\displaystyle{ \left \{ \epsilon,T \right \} }[/math],是一种模式发现机器,其中[math]\displaystyle{ \epsilon }[/math]是因果态函数,可以将状态[math]\displaystyle{ s }[/math]映射到[math]\displaystyle{ \epsilon(s) }[/math], [math]\displaystyle{ T }[/math]是通过[math]\displaystyle{ \epsilon }[/math]定义的状态转移矩阵的集合。通过证明[math]\displaystyle{ \epsilon-machine }[/math]具有最大可预测性、最小统计复杂度以及最小随机性这三个重要特性验证了其在某种意义上是最优的。此外,作者引入了一种分层机器重构算法可以从观测数据中计算因果态和[math]\displaystyle{ \epsilon-machine }[/math]。尽管该算法可能并不适用于所有场景,但作者以混沌动力学、隐马尔可夫模型和元胞自动机为例,给出了数值计算结果和相应的机器重构路径。虽然该方法没有给出涌现的明确定义和定量理论,但是随后一些研究人员进一步推进了计算力学的发展,Shalizi等[29]在自己的工作中讨论计算力学与涌现的关系,同时作者解释说,涌现可以被理解为一个动力学过程,在这个过程中,一个模式获得了能适应不同环境的能力。
因果涌现框架与计算力学存在很多相似之处,所有历史过程[math]\displaystyle{ \overleftarrow{s} }[/math]可以看作是微观状态,所有[math]\displaystyle{ R \in \mathcal{R} }[/math]表示宏观状态,函数[math]\displaystyle{ \eta }[/math]可以理解为一种粗粒化函数,因果态[math]\displaystyle{ \epsilon \left ( \overleftarrow{s} \right ) }[/math]是一种特殊状态,它至少可以与微观状态[math]\displaystyle{ \overleftarrow{s} }[/math]具有相同的预测能力,因此,[math]\displaystyle{ \epsilon }[/math]可以理解为一种有效的粗粒化策略,因果转移[math]\displaystyle{ T }[/math] 对应于有效的宏观动力学。最小随机性特征表征了宏观动力学的确定性,在因果涌现中可以用有效信息衡量。
G-emergence
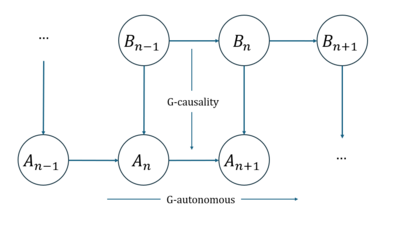
G-emergence理论是Seth于2008年提出的,最早从因果的角度对涌现进行定量量化的研究之一[28],基本思想是用非线性格兰杰因果来量化复杂系统中的弱涌现。具体来说,如果我们使用二元自回归模型进行预测,当只存在两个变量A和B时,自回归模型存在两个等式,每个等式对应其中一个变量每个时刻的值,每个变量的当前时刻值都是由自身变量和另外一个变量在滞后时间范围内的数值以及残差项构成,残差可以理解为预测误差,残差可以用来衡量格兰杰因果(G-causality)的因果效应程度。B作为A的格兰杰因(G-cause)的程度通过两个残差方差之比的对数来计算,其中一个是在省略B时A的自回归模型的残差,另一个是全预测模型(包含了A和B)的残差。此外,作者还定义了G-autonomous,表示一个时间序列的过去值可以帮助预测自身的未来值的程度度量,可以用类似量化格兰杰因果的方法来刻画。
基于上述G-causality中的两个基本概念,可以来判断涌现的发生(这里是基于格兰杰因果的涌现的衡量,记作G-emergence)。如果把A理解为宏观变量,B理解为微观变量。发生涌现的条件包含两个:1)A是关于B的G-autonomous;2)B是A的G-cause。其中G-emergence的程度是通过A的G-autonomous的程度与B的平均G-cause的程度的乘积来计算。Seth提出的G-emergence理论首次尝试使用因果关系来量化涌现现象,然而,作者使用的因果关系是格兰杰因果,这不是一个严格的因果关系,同时结果也取决于所使用的回归方法。此外,方法的度量指标是根据变量而不是动力学定义的,这意味着结果会依赖于变量的选择。这些都构成了G-emergence理论的弊端。
因果涌现框架与前面提到的G-emergence也有相似之处,两个方法的宏观状态都需要人工选择。此外,需要注意的是,上述的一些定量量化涌现的方法往往没有考虑因果关系,最接近的也只是使用格兰杰因果不是真正的因果。
其他定量刻画涌现的理论
此外,也存在一些其他的涌现定量理论,主要有两种方法被广泛讨论。一种是从无序到有序的过程来理解涌现,Moez Mnif和Christian Müller-Schloer[30]使用香农熵来度量有序和无序。在自组织过程中,当秩序增加时就会出现涌现,通过测量初始状态和最终状态之间的香农熵的差异来计算秩序的增加,然而该方法存在一些缺陷:依赖于抽象的观察水平以及系统初始条件的选择,为了克服这两种困难,作者提出了一种与最大熵分布相比的度量香农熵的相对水平的方法。受Moez mif和Christian Müller-Schloer工作的启发,参考文献[31]建议使用两个概率分布之间的散度能更好地量化涌现。他们将涌现理解为在所观察到的样本基础上的一种意想不到的或不可预测的分布变化。但该方法存在计算量大、估计精度低等缺点。为了解决这些问题,文献[32]进一步提出了一种使用高斯混合模型估计密度的近似方法,并引入马氏距离来表征数据与高斯分量之间的差异,从而得到了更好的结果。此外,Holzer和de Meer[33][34]等人提出了另一种基于Shannon熵的涌现测量方法。他们认为一个复杂的系统是一个自组织的过程,在这个过程中,不同的个体通过通信相互作用。然后,我们可以根据代理之间所有通信的香农熵度量与作为单独源的每次通信的香农熵总和之间的比率来测量涌现。
另一种方法是从“整体大于部分之和”的角度来理解涌现[35][36],该方法定义来自交互规则和代理状态的涌现,而不是整个系统的总体统计度量。具体地说,这个度量由两个相互相减的项组成。第一项描述了整个系统的集体状态,而第二项代表了所有组成部分的单个状态的总和,该度量强调涌现产生于系统的相互作用和集体行为。
基于有效信息的因果涌现理论
历史上,第一个比较完整而明确的利用因果来定义涌现的定量理论当属Erik Hoel, Larissa Albantakis以及Giulio Tononi三人提出的因果涌现理论[1][2]。该理论针对马尔科夫链定义所谓的因果涌现为:粗粒化后的马尔科夫链比原始的马尔科夫链具有更大的因果效应强度的现象。这里,因果效应强度是通过有效信息来衡量的,该指标是对互信息指标的一种改造,主要差别是将t时刻的状态变量进行了do干预,干预成了均匀分布(或最大熵分布)。有效信息指标早在2003年就被Giulio Tononi在研究整合信息论的时候提出。
基于信息分解的因果涌现理论
此外,2010年,Rosas等[37]从信息理论视角出发,提出一种基于信息分解方法来定义系统中的因果涌现,基于协同信息或者冗余信息来定量的刻画涌现。所谓的信息分解是分析复杂系统中各个变量复杂相互关系的一种新方法。
近期工作
2024年,张江等人[26]基于奇异值分解,提出了一套新的因果涌现理论。该理论的核心思想是指出所谓的因果涌现其实等价于动力学可逆性的涌现。给定一个系统的马尔科夫转移矩阵,通过对它进行奇异值分解,将奇异值的[math]\displaystyle{ \alpha }[/math]次方的和定义为马尔科夫动力学的可逆性度量([math]\displaystyle{ \Gamma_{\alpha}\equiv \sum_{i=1}^N\sigma_i^{\alpha} }[/math]),该指标与有效信息具有高度的相关性,也可以用于刻画动力学的因果效应强度。根据奇异值的谱,该方法可以在不显式定义粗粒化方案的条件下,直接定义所谓清晰涌现和模糊涌现的概念。
Barnett等[38]人基于转移熵,通过判断宏观动力学与微观动力学进行解耦来判断涌现的发生,因而提出了动力学解耦的概念。
因果涌现的量化
接下来,我们重点介绍几种利用因果度量来量化涌现现象的研究。
几种因果涌现理论
对于如何定义因果涌现是一个关键问题,有几个代表性工作,分别是Hoel等[1][2]提出的基于有效信息的方法、Rosas等[37]提出的基于信息分解的方法、张江等人[26]基于奇异值分解提出了一套新的因果涌现理论以及一些其他的理论。
Erik Hoel的因果涌现理论
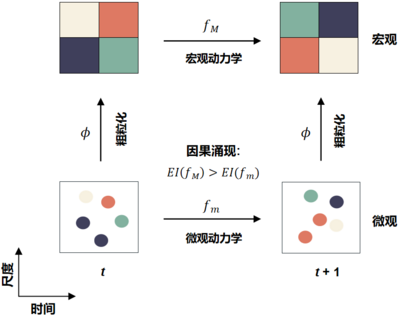
Hoel等于2013年[1][2]提出因果涌现理论,下图是对该理论的一个抽象框架,其中,横坐标表示时间,纵坐标表示尺度(Scale)。该框架可以看成是对同一个动力系统在微观和宏观两种尺度上的描述。其中,[math]f_m[/math]表示微观动力学,[math]f_M[/math]表示宏观动力学,二者通过一个粗粒化函数[math]\phi[/math]相连。在一个离散状态的马尔科夫动力系统中,[math]f_m[/math]和[math]f_M[/math]都是马尔科夫链,对[math]f_m[/math]进行马尔科夫链的粗粒化,就可以得到[math]f_M[/math]。[math]\mathcal{J}[/math]为有效信息([math]\displaystyle{ EI }[/math])的度量。由于微观态可能具有更大的随机性,这导致微观动力学的因果性比较弱,所以通过对每一个时刻的微观态进行合理的粗粒化,就有可能得到因果性更强的宏观态。所谓的因果涌现,就是指当我们对微观态进行粗粒化的时候,宏观动力学的有效信息会增加这一现象,并且宏观态与微观态的有效信息之差被定义为因果涌现的强度。
有效信息(EI)最早由Tononi等人在整合信息论的研究中提出[39]。在因果涌现研究中,Erik Hoel等人将这种因果效应度量指标用于量化一个因果机制的因果性强弱。
具体来说,EI的计算为:使用干预操作对自变量做干预,并考察在这一干预下,因和果变量之间的互信息,这种互信息就是有效信息,即因果机制的因果效应度量。
在马尔科夫链中,任意时刻的状态变量[math]X_t[/math]都可以看作是原因,而下一时刻的状态变量[math]X_{t+1}[/math]就可以看作是结果,这样马尔科夫链的状态转移矩阵就是它的因果机制。因此,针对马尔科夫链的[math]\displaystyle{ EI }[/math]的计算公式如下所示:
[math]\displaystyle{ \begin{aligned} EI(f) \equiv& I(X_t,X_{t+1}|do(X_t)\sim U(\mathcal{X}))\equiv I(\tilde{X}_t,\tilde{X}_{t+1}) \\ &= \frac{1}{N}\sum^N_{i=1}\sum^N_{j=1}p_{ij}\log\frac{N\cdot p_{ij}}{\sum_{k=1}^N p_{kj}} \end{aligned} }[/math]
其中f表示一个马尔科夫链的状态转移矩阵,[math]U(\mathcal{X})[/math]表示状态变量[math]X_t[/math]取值空间[math]\mathcal{X}[/math]上的均匀分布。[math]\displaystyle{ \tilde{X}_t,\tilde{X}_{t+1} }[/math]分别为把t时刻的[math]X_t[/math]干预为均匀分布后,前后两个时刻的状态。[math]\displaystyle{ p_{ij} }[/math]为第i个状态转移到第j个状态的转移概率。从这个式子不难看出,EI仅仅是概率转移矩阵[math]f[/math]的函数。进行干预操作是为了使得有效信息能客观衡量动力学的因果特性而不受原始输入数据的分布影响。
有效信息可以拆解为确定性和简并性两部分,还可以通过引入归一化从而消除状态空间规模大小的影响。关于有效信息的详细信息请参看词条:有效信息。
我们可以通过比较系统中宏微观动力学的有效信息大小来判断因果涌现的发生:
[math]\displaystyle{ CE=EI\left ( f_M \right )-EI\left (f_m \right ) }[/math]
其中CE为因果涌现强度。如果宏观动力学的有效信息大于微观动力学的有效信息(也就是[math]\displaystyle{ CE\gt 0 }[/math]),那么我们认为在该粗粒化基础上宏观动力学具有因果涌现特性。
在文献[1]中,Hoel给出一个含有8个状态的马尔科夫链的状态转移矩阵([math]f_m[/math]的例子,如图a所示。其中前7个状态之间等概率转移,最后一个状态是独立的,只能转变为自身的状态。
对该矩阵的粗粒化为如下操作:首先,将前7个状态归并为一个宏观状态,不妨称为A,并且将[math]f_m[/math]中前7行的前7列的概率数值加总得到A到A状态转移的概率,并对[math]f_m[/math]矩阵的其它数值保持不变。这样归并后的新的概率转移矩阵如右图所示,记为[math]f_M[/math]。这是一个确定的宏观马尔科夫转移矩阵,即系统的未来状态完全可以由当前状态决定。此时[math]\displaystyle{ EI(f_M\ )\gt EI(f_m\ ) }[/math],系统发生了因果涌现。
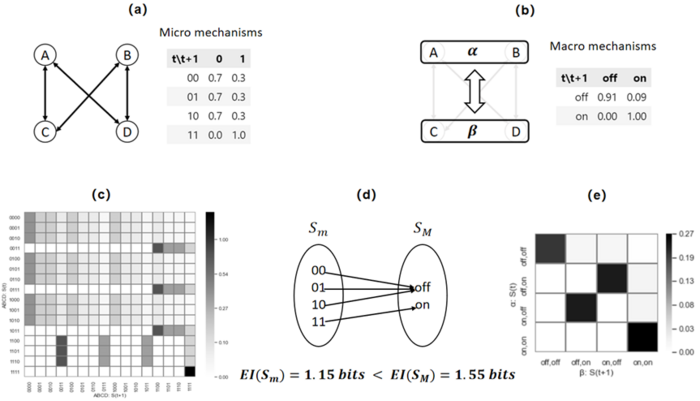
另一个文献[1]中的例子是一个布尔网络中发生因果涌现的例子。如图所示,这是一个含有4个节点的布尔网络,每个节点有0和1两种状态,每个节点与另外两个节点相连,遵循相同的微观动力学机制(a图)。因此,该系统一共含有十六个微观状态,它的动力学可以用一个[math]\displaystyle{ 16\times16 }[/math]的状态转移矩阵(c图)表示。
进一步,如果我们给定分组方式,如将A和B进行合并,C和D进行合并(如b图所示),同时给定微观状态到宏观状态的映射函数(如d图所示),就可以得到一个新的宏观的布尔网络以及它的动力学机制,根据这个机制就可以得到宏观网络的状态转移矩阵(如e图所示)。通过对比,我们发现宏观动力学的有效信息大于微观动力学的有效信息([math]\displaystyle{ EI(f_M\ )\gt EI(f_m\ ) }[/math]),该系统发生了因果涌现。
进一步,在[40]一文中,Hoel等人提出了因果几何理论框架,试图将因果涌现理论推广到具有连续状态的马尔科夫动力系统之中,该文章对随机函数映射定义了EI,同时还引入了干预噪音和因果几何的概念,并将这一概念与信息几何进行了对照和类比。刘凯威等人[41]又进一步给出了随机迭代动力系统的精确解析的因果涌现理论。
Rosas的因果涌现理论
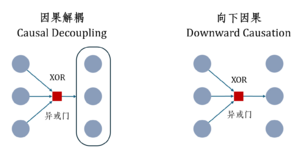
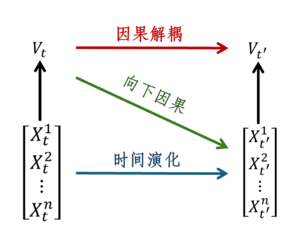
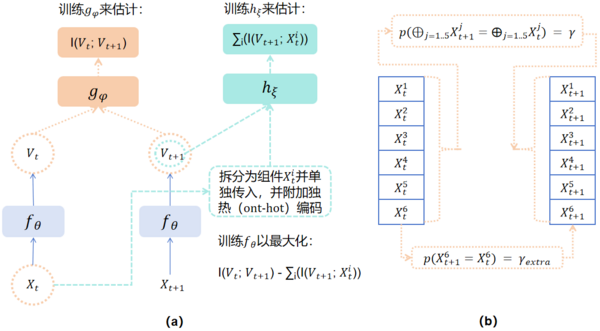
Hoel提出的基于粗粒化的方法来量化系统中的因果涌现需要预先提供系统的状态转移矩阵以及粗粒化策略,然而现实情况是,往往只能获得系统的观测数据。为了克服这两个困难,Rosas等[37]从信息论视角出发,提出一种基于信息分解方法来定义系统中的因果涌现,这里发生因果涌现有两种可能性:因果解耦(Causal Decoupling)和向下因果(Downward Causation),其中因果解耦表示宏观态对其他宏观态的因果效应,向下因果表示宏观态对于微观元素的因果效应。具体地,定义微观状态输入为[math]\displaystyle{ X_t\ (X_t^1,X_t^2,…,X_t^n ) }[/math],[math]\displaystyle{ V_t }[/math]表示宏观状态是[math]\displaystyle{ X_t }[/math]的随附特征,[math]\displaystyle{ X_{t+1} }[/math]和[math]\displaystyle{ V_{t+1} }[/math]分别表示下一时刻的微观和宏观状态。
该方法建立在Williams和Beer等[42]提出的多元信息非负分解的基础上,Beer使用偏信息分解(PID)将微观态[math]\displaystyle{ X(X^1,X^2 ) }[/math]与宏观态[math]\displaystyle{ V }[/math]之间的互信息分解为四个部分,计算公式如下所示:
[math]\displaystyle{ I(X^1,X^2;V)=Red(X^1,X^2;V)+Un(X^1;V│X^2 )+Un(X^2;V│X^1 )+Syn(X^1,X^2;V) }[/math]
其中[math]\displaystyle{ Red(X^1,X^2;V) }[/math]表示冗余信息,是指两个微观态[math]\displaystyle{ X^1 }[/math]和[math]\displaystyle{ X^2 }[/math]同时给宏观态[math]\displaystyle{ V }[/math]提供的信息;[math]\displaystyle{ Un(X^1;V│X^2 ) }[/math]和[math]\displaystyle{ Un(X^2;V│X^1 ) }[/math]表示特有信息,是指每一个微观态单独给宏观态提供的信息;[math]\displaystyle{ Syn(X^1,X^2;V) }[/math]表示协同信息,是指所有微观态[math]\displaystyle{ X }[/math]联合给宏观态[math]\displaystyle{ V }[/math]提供的超过各自给宏观态提供的信息。
然而,PID框架只能分解关于多个原变量和一个目标变量之间的互信息,Rosas扩展了该框架,提出整合信息分解方法[math]\displaystyle{ \Phi ID }[/math][43]来处理多个原变量和多个目标变量之间的互信息,可以用来分解不同时刻间的互信息,作者基于分解后的信息提出了两种因果涌现的定义方法:
1)当特有信息[math]\displaystyle{ Un(V_t;X_{t+1}| X_t^1,\ldots,X_t^n\ )\gt 0 }[/math],表示当前时刻的宏观态[math]\displaystyle{ V_t }[/math]能超过当前时刻的微观态[math]\displaystyle{ X_t }[/math]给下一时刻的整体系统[math]\displaystyle{ X_{t+1} }[/math]再多提供一些信息,存在因果涌现;
2)绕开了选择特定的宏观态[math]\displaystyle{ V_t }[/math],仅仅基于系统当前时刻的微观态[math]\displaystyle{ X_t }[/math]和下一时刻的微观态[math]\displaystyle{ X_{t+1} }[/math]之间的协同信息定义因果涌现,当协同信息[math]\displaystyle{ Syn(X_t^1,…,X_t^n;X_{t+1}^1,…,X_{t+1}^n )\gt 0 }[/math],系统发生了因果涌现。其中[math]\displaystyle{ Syn(X_t;X_{t+1}\ ) ≥ Un(V_t;X_{t+1}| X_t\ ) }[/math]衡成立。
值得注意的是,对于方法一判断因果涌现的发生需要依赖宏观态[math]\displaystyle{ V_t }[/math]的选择,其中方法一是方法二的下界,所以,如果[math]\displaystyle{ Un(V_t;X_{t+1}| X_t\ ) }[/math]大于0,则出现因果涌现,然而[math]\displaystyle{ V_t }[/math]的选择又是很困难的,因此该方法不可行。一种自然的想法就是使用第二种方法借助协同信息来判断因果涌现的发生,但是由于冗余信息存在计算的问题,而协同信息的计算又依赖冗余信息。因此,第二种方法基于协同信息的计算往往也是不可行的。总之,这两种因果涌现的定量刻画方法都存在一些缺点,因此,更加合理的量化方法有待提出。
文中作者举了一个前后两个时间序列数据的奇偶是否相同的例子来说明什么时候发生因果解耦、向下因果以及因果涌现。当第二个判断条件中只有第一项成立时是用来判断向下因果条件,只有第二项成立时是用来判断因果解耦条件,两种同时成立时用来判断因果涌现条件。这里,[math]\displaystyle{ X_t=(X_t^1,…,X_t^n )\in \left\{0,1\right\}^n }[/math],宏观态是微观输入的异或结果。
基于可逆性的因果涌现理论
张江等人[26]基于奇异值分解,提出了一套新的因果涌现理论。给定一个系统的马尔科夫转移矩阵[math]\displaystyle{ P }[/math],通过对它进行奇异值分解,得到两个正交且的归一化矩阵[math]\displaystyle{ U }[/math]和[math]\displaystyle{ V }[/math],和一个对角阵[math]\displaystyle{ \Sigma }[/math]:[math]\displaystyle{ P= U\Sigma V^T }[/math]
我们可以将奇异值的[math]\displaystyle{ \alpha }[/math]次方的和定义为马尔科夫动力学的可逆性度量,即: [math]\displaystyle{ \Gamma_{\alpha}\equiv \sum_{i=1}^N\sigma_i^{\alpha} }[/math]
这里,[math]\Gamma_{\alpha}[/math]为近似动力学可逆性指标,[math]\sigma_i[/math]为概率转移矩阵[math]\displaystyle{ P }[/math]的奇异值,并且按照从大到小的顺序排列,[math]\alpha\in(0,2)[/math]为一个指定的参数,它起到让[math]\Gamma_{\alpha}[/math]能够更多地反映确定性还是简并性这样一种权重或倾向性。通常情况下,我们取[math]\alpha=1[/math],这可以让[math]\Gamma_{\alpha}[/math]能够在确定性与简并性之间达到一种平衡。
此外,文献中作者证明了EI与动力学可逆性[math]\Gamma_{\alpha}[/math]之间存在着一种近似的关系:
[math]\displaystyle{ EI\sim \log\Gamma_{\alpha} }[/math]
如果[math]\displaystyle{ P }[/math]的秩为[math]\displaystyle{ r }[/math],即从第[math]\displaystyle{ r+1 }[/math]个奇异值开始,奇异值都为0,则我们称动力学[math]\displaystyle{ P }[/math]存在着清晰的因果涌现(Clear Causal Emergence),并且因果涌现的数值为:[math]\displaystyle{ \Delta \Gamma_{\alpha} = \Gamma_{\alpha}(1/r-1/N) }[/math]
如果矩阵[math]\displaystyle{ P }[/math]满秩,但是对于任意给定的小数[math]\displaystyle{ \epsilon }[/math],存在[math]\displaystyle{ r }[/math],使得从[math]\displaystyle{ r+1 }[/math]开始,所有的奇异值都小于[math]\displaystyle{ \epsilon }[/math],则称系统存在着程度的模糊的因果涌现(Vague Causal Emergence),且因果涌现的数值为:[math]\displaystyle{ \Delta \Gamma_{\alpha}(\epsilon) = \frac{\sum_{i=1}^{r} \sigma_{i}^{\alpha}}{r} - \frac{\sum_{i=1}^{N} \sigma_{i}^{\alpha}}{N} }[/math]
总结来看,该定量化因果涌现的方法好处在于不依赖于具体的粗粒化策略,因而可以更加客观地量化因果涌现。其缺点是不能像[math]\displaystyle{ EI }[/math]那样分解为确定度和简并度两个分量,并且该方案需要事先给定系统的动力学。
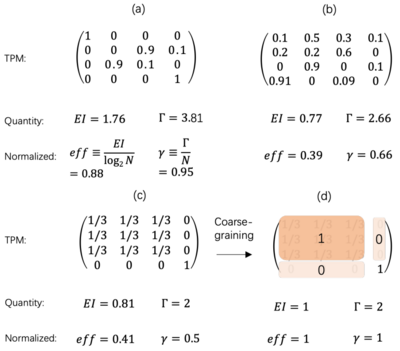
文中作者对比了状态转移矩阵的[math]\displaystyle{ EI }[/math]和[math]\displaystyle{ \Gamma }[/math],对比图a,b发现对于不同的状态转移矩阵,[math]\displaystyle{ EI }[/math]降低,[math]\displaystyle{ \Gamma }[/math]也同步降低。进一步对比粗粒化前后的效果,其中图d是对图c状态转移矩阵的粗粒化,对比归一化后的指标发现,由于粗粒化后的宏观状态转移矩阵是一个确定性系统,因此,在指标[math]\displaystyle{ eff }[/math]和[math]\displaystyle{ \gamma }[/math]都达到了最大值1。
其他(Dynamic independence等)
动力学解耦(Dynamic Independence)是一种表征粗粒化宏观变量相对于微观动力学系统的独立性的方法[38]。其核心思想是,尽管宏观变量由微观变量组成,但在预测宏观变量未来状态时,微观历史并不能提供额外的信息。动力学解耦从信息论角度形式化了这种简并性,并通过转移熵(Transfer Entropy)进行量化。
1. 基本定义
动力学解耦表明,在自身历史条件下,宏观变量 Υ 是独立于微观变量 X 的历史。用公式表示为:
[math]\displaystyle{ I(Y_t : X^-_t | Y^-_t) = 0 }[/math]
2. 转移熵表示:
当且仅当时间 t 从 X 到 Y 的传输熵 [math]\displaystyle{ T_t(X \to Y) }[/math]为零时,Y 是相对于 X 动力学解耦的:
[math]\displaystyle{ Y \text{ 在时间 } t \text{ 相对于 } X \text{ 动力学解耦} \Leftrightarrow T_t(X \to Y) = 0 }[/math]
转移熵 [math]\displaystyle{ T_t(X \to Y) }[/math]定义为:
[math]\displaystyle{ T_t(X \to Y) = H(Y_t | Y^-_t) - H(Y_t | Y^-_t, X^-_t) }[/math]
3. 带有环境的情况:
在包含环境过程 E 的情况下,定义转移熵为:
[math]\displaystyle{ T_t(X \to Y | E) = I(Y_t : X^-_t | Y^-_t, E^-_t) = H(Y_t | Y^-_t, E^-_t) - H(Y_t | X^-_t, Y^-_t, E^-_t) }[/math]
宏观变量 Y 在环境 E 的条件下相对于微观系统 X 动力学解耦,当且仅当:
[math]\displaystyle{ T_t(X \to Y | E) = 0 }[/math]
动力学解耦的性质
- 预测解释: 动力学独立性可以通过预测性来解释:给定自身历史的情况下,过程 Y 在时间 t 的不可预测性由条件熵 H(Yt∣Yt−) 量化。而动力学依赖性 Tt(X→Y) 量化了 X 对 Y 的预测超出 Y 自身预测的程度。
- 信息论条件: 动力学独立性与香农条件互信息直接相关,通过互信息可以衡量系统中变量之间的信息传递。
- 推广: 动力学独立性可以推广到包含第三个条件变量的情况,通过条件转移熵来衡量。对于确定性系统,需要采用不同的方法进行框架化。
动力学独立的概念广泛适用于多种复杂动态系统,包括神经系统、经济过程和进化过程。通过粗粒化方法,可以将高维微观系统简化为低维宏观系统,从而揭示出复杂系统中的突现结构。
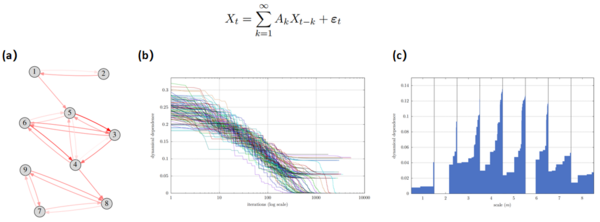
文中,作者在线性系统中进行了实验验证,实验流程是:1)使用线性系统生成参数与规律;2)设定粗粒化函数;3)得到转移熵的表达式;4)优化求解最大脱耦合率的粗粒化方法(对应最小转移熵)。这里的优化算法可以使用转移熵作为优化目标,然后使用梯度下降算法来求解符合的粗粒化函数,也可以使用遗传算法来优化。上图展示了一个线性系统的例子,动力学是一个向量自回归的模型,图a是一个格兰杰因果网络,图b是使用遗传算法不同的初始化迭代的结果,纵轴表示动力学解耦的程度,图c表示不同的粗粒化尺度会影响能否优化到动力学解耦的程度,结果发现只有scale=2和6时可能达到动力学解耦,因此尺度的选择也很重要。
几种因果涌现理论比较
| 方法 | 是否考虑因果 | 是否涉及粗粒化 | 适用的动力学系统 | 度量指标 |
|---|---|---|---|---|
| Hoel的因果涌现理论 | 考虑了,引入do干预 | 考虑了粗粒化,但是需要人为选择 | 离散马尔科夫动力学 | 有效信息 |
| Rosas的因果涌现理论 | 未考虑,只是互信息的组合 | 基于协同信息判断时不涉及粗粒化,基于冗余信息计算也涉及宏观态的选择 | 任意动力学 | 协同信息与冗余信息 |
| 基于可逆性的因果涌现理论 | 未考虑 | 不依赖于具体的粗粒化策略 | 离散马尔科夫动力学 | [math]\displaystyle{ \Gamma }[/math] |
| Dynamic independence | 只是格兰杰因果,不知真正的因果 | 涉及,基于梯度下降求解线性变换(粗粒化函数) | 任意动力学 | 转移熵 |
因果涌现的识别
前面已经介绍了一些通过因果关系和其他信息理论概念来量化涌现的工作。然而,在实际应用中,往往只能收集到观测数据,无法得到系统的真实动力学。因此,从可观测数据中辨别系统中因果涌现的发生是一个更为重要的问题。此外,在因果涌现的识别问题中往往希望寻找一个最优的宏观尺度,使其有效信息达到最大值,此时的系统具有最大因果力,并且能以最可靠、最有效的方式预测未来的状态。下面介绍两种因果涌现的识别方法,包括基于互信息的近似方法和神经信息压缩方法。
基于互信息的近似方法
由于基于互信息的近似方法需要依赖宏观态[math]\displaystyle{ V }[/math]的选择,因此,作者给出了两种方法,一种是给定一个宏观态[math]\displaystyle{ V }[/math]计算,另一种是基于机器学习的方法学习宏观态[math]\displaystyle{ V }[/math]以及最大化[math]\displaystyle{ \mathrm{\Psi} }[/math]。下面我们分别介绍这两种方法:
Rosas虽然给出因果涌现的严格定义,但在[math]\displaystyle{ \varphi ID }[/math]中使用的数学公式很复杂,同时计算要求很高,信息分解框架中定义的信息原子难以计算, 难以将该方法应用于实际系统。因此,Rosas等绕开特有信息和协同信息的计算[37],作者推导出只需要计算互信息的近似公式,提出一个判定因果涌现发生的充分条件,基于互信息提出三个新指标,[math]\displaystyle{ \mathrm{\Psi} }[/math] ,[math]\displaystyle{ \mathrm{\Delta} }[/math] 和[math]\displaystyle{ \mathrm{\Gamma} }[/math]用于识别系统中的因果涌现,三种指标的具体计算公式如下所示:
[math]\displaystyle{ \Psi_{t, t+1}(V):=I\left(V_t ; V_{t+1}\right)-\sum_j I\left(X_t^j ; V_{t+1}\right) }[/math]
其中[math]\displaystyle{ X_t^j }[/math]表示第 j 维t时刻的微观变量,[math]\displaystyle{ V_t ; V_{t+1} }[/math]代表两个连续时间的宏观状态变量,当[math]\displaystyle{ \mathrm{\Psi}\gt 0 }[/math]时,宏观状态会发生涌现,但是当[math]\displaystyle{ \mathrm{\Psi}\lt 0 }[/math],我们不能确定[math]\displaystyle{ V }[/math]是否发生涌现。
[math]\displaystyle{ \Delta_{t, t+1}(V):=\max _j\left(I\left(V_t ; X_{t+1}^j\right)-\sum_i I\left(X_t^i ; X_{t+1}^j\right)\right) }[/math]
当[math]\displaystyle{ \mathrm{\Delta}\gt 0 }[/math]时,宏观状态[math]\displaystyle{ V }[/math]发生向下因果。
[math]\displaystyle{ \Gamma_{t, t+1}(V):=\max _j I\left(V_t ; X_{t+1}^j\right) }[/math]
当[math]\displaystyle{ \mathrm{\Delta}\gt 0 }[/math]且[math]\displaystyle{ \mathrm{\Gamma}=0 }[/math]时,宏观状态[math]\displaystyle{ V }[/math]发生因果涌现且发生因果解耦。
使用[math]\displaystyle{ \mathrm{\Psi} }[/math]来识别因果涌现的发生是因为[math]\displaystyle{ \mathrm{\Psi} }[/math]又是特有信息的下界,有如下关系: [math]\displaystyle{ Un(V_t;X_{t+1}|X_t) ≥ I\left(V_t ; V_{t+1}\right)-\sum_j I\left(X_t^j ; V_{t+1}\right) + Red(V_t, V_{t+1};X_t) }[/math]
由于[math]\displaystyle{ Red(V_t, V_{t+1};X_t) }[/math]为非负数,所以提出一个充分非必要条件[math]\displaystyle{ \Psi_{t, t+1}(V) }[/math]。当[math]\displaystyle{ \Psi_{t, t+1}(V) \gt 0 }[/math],系统发生因果涌现。
该方法因为是基于格兰杰因果,所以计算比较方便,且对系统的动力学没有马尔科夫性的假设和要求,同时该方法避开讨论粗粒化策略。但是也存在很多缺点:1)该方法提出的三个指标 ,[math]\displaystyle{ \mathrm{\Psi} }[/math] ,[math]\displaystyle{ \mathrm{\Delta} }[/math] 和[math]\displaystyle{ \mathrm{\Gamma} }[/math]只是基于互信息计算没有考虑因果,同时该方法得到的仅仅是发生因果涌现的充分条件;2)该方法无法得到显式的宏观动力学以及粗粒化策略,然而这两项对于下游的任务往往十分重要,同时该方法需要手动给定粗粒化策略和宏观变量,而不同的选择会对结果造成显著影响;3)当系统具有大量冗余信息或具有许多变量时,该方法的计算复杂度仍然很高,由于[math]\displaystyle{ \Psi }[/math]作为近似条件,高维系统中误差非常大,很容易得到负值,从而无法判断是否有因果涌现发生。因此,该方法不是一种最优的方法,基于数据驱动的神经信息压缩方法应运而生。
为了验证猕猴运动有关的信息是其皮层活动的一个涌现特征,Rosas等做了如下实验:基于猕猴的皮质脑电图(ECoG)和动作捕捉(MoCap)数据,其中 ECoG 和 MoCap 分别由 64 个通道和 3 个通道的数据构成微观和宏观数据;由于最原始的 MoCap 数据不满足随附特征的条件独立假设,因此,他们利用偏最小二乘和支持向量机算法,推断出与预测猕猴行为有关的编码在 ECoG 信号中的那部分神经活动,并推测该信息是潜在神经活动的涌现特征;基于计算所得宏观特征与微观状态,验证了因果涌现的存在。
Kaplanis等人[26]基于机器学习的方法学习宏观态[math]\displaystyle{ V }[/math]以及最大化[math]\displaystyle{ \mathrm{\Psi} }[/math]:使用[math]\displaystyle{ f_{\theta} }[/math]神经网络来学习将微观输入[math]\displaystyle{ X_t }[/math]粗粒化成宏观输出[math]\displaystyle{ V_t }[/math],同时使用神经网络[math]\displaystyle{ g_{\phi} }[/math]和[math]\displaystyle{ h_{\xi} }[/math]来分别学习[math]\displaystyle{ I(V_t;V_{t+1}) }[/math]和[math]\displaystyle{ \sum_i(I(V_{t+1};X_{t}^i)) }[/math]两者互信息的计算,最后通过最大化两者之间的差(即[math]\displaystyle{ \mathrm{\Psi} }[/math])来优化学习。
神经信息压缩方法
近年来,新兴的人工智能技术已经攻克一系列重大难题,同时机器学习方法配备了各种精心设计的神经网络结构和自动微分技术,可以在巨大的函数空间中逼近任何函数。因此,张江等[44]尝试基于神经网络提出了一种基于数据驱动的能够从时间序列数据中识别系统中的因果涌现方法,该方法能自动提取有效的粗粒化策略和宏观动力学,克服了信息分解方法中的种种不足。
在该工作中,输入的是时间序列数据[math]\displaystyle{ (X_1,X_2,...,X_T ) }[/math],可以使用如下的微分方程表示:
[math]\displaystyle{ \frac{d X}{d t}=f(X(t), \xi) }[/math]
其中[math]\displaystyle{ \xi }[/math]表示系统中的噪音。
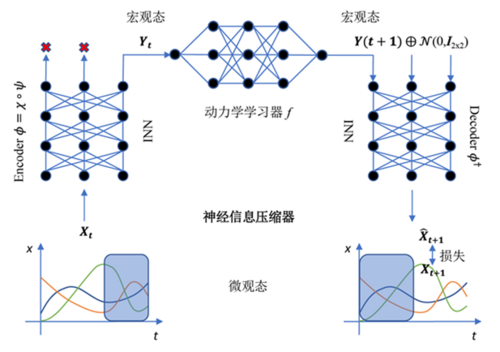
为了识别系统中的因果涌现,作者提出一种神经信息压缩器(NIS)方法,构建Encoder-Dynamic Learning-Decoder框架,该模型由编码器、动力学学习器以及解码器三个部分构成,用神经网络构建动力学学习器([math]\displaystyle{ f }[/math]),用可逆神经网络(INN)构建编码器(Encoder)和解码器(Decoder)。该模型框架可以看成是一个神经信息压缩器,将包含噪音的微观态压缩成宏观态,丢弃无用的信息,从而使得宏观动力学的因果性更强。NIS方法的模型框架如图所示。
具体来说,模型输入是微观状态[math]\displaystyle{ X_t\ (X_t^1,X_t^2,…,X_t^p ) }[/math],[math]\displaystyle{ p }[/math]表示输入数据的维数,输出预测下一个时刻的微观状态[math]\displaystyle{ \hat{X}_{t+1}\left(\hat{X}_{t+1}^1, \hat{X}_{t+1}^2, \ldots, \hat{X}_{t+1}^p\right) }[/math],该方法的目标函数是希望保证微观状态预测误差很小的条件下最大化有效信息,在保证预测误差约束足够小的情况下,NIS方法可以避免平凡解的出现。具体计算公式如下所示:
[math]\displaystyle{ \max _{\phi_q, \hat{f}_q, \phi_q^{\dagger}, q} E I\left(f_{\phi_q}\right) \quad \text{s.t.}\left\|\phi_q^{\dagger}(Y(t+1))-X_{t+1}\right\|\lt \epsilon }[/math]
最终希望得到有效的粗粒化维度[math]\displaystyle{ q }[/math]、粗粒化策略[math]\displaystyle{ \mathrm{\phi}_q }[/math]和宏观动力学[math]\displaystyle{ {\hat{f}}_{\mathrm{\phi}_q} }[/math],然而由于该目标函数是一个泛函优化问题,往往很难优化。为了解决这个问题,作者将优化过程分为两个阶段,第一个阶段表示在给定宏观尺度[math]\displaystyle{ q }[/math]的情况下[math]\displaystyle{ \min _{\phi_q, \hat{f}_q, \phi_q^{\dagger}}\left\|\phi_q^{\dagger}(Y(t+1))-X_{t+1}\right\|\lt \epsilon }[/math],第二阶段将复杂的函数优化问题转换成线性搜索不同的[math]\displaystyle{ q }[/math],使得找到有效信息最大的宏观尺度[math]\displaystyle{ \mathop{max}\limits_{q}EI(\hat{f}_{\phi_q}^\ast) }[/math] 。
除了能基于时序数据自动识别因果涌现,该框架还有很好的理论证明,其中有两个重要定理,定理一:神经信息挤压器的信息瓶颈,即对于任意的双射[math]\displaystyle{ \mathrm{\Psi}_\alpha }[/math]、投影[math]\displaystyle{ \chi_q }[/math]、宏观动力学[math]\displaystyle{ f }[/math]以及高斯噪音[math]\displaystyle{ z_{p-q}\simΝ\left (0,I_{p-q}\right ) }[/math],[math]\displaystyle{ I\left(Y_t;Y_{t+1}\right)=I\left(X_t;{\hat{X}}_{t+1}\right) }[/math]恒成立,这意味着,编码器丢弃的所有信息实际上都是与预测无关的纯粹噪声;定理二:对于一个训练好的模型,[math]\displaystyle{ I\left(X_t;{\hat{X}}_{t+1}\right)\approx I\left(X_t;X_{t+1}\right) }[/math]。因此,综合定理一和定理二,可以得到对于一个训练好的模型[math]\displaystyle{ I\left(Y_t;Y_{t+1}\right)\approx I\left(X_t;X_{t+1}\right) }[/math]。
该工作的一个重要优点就是该框架能同时处理离散和连续动力学系统,通过将神经网络看作是给定输入条件下的高斯分布[math]\displaystyle{ p\left(Y| X\right) }[/math],可以定义新的有效信息计算公式,公式如下见有效信息词条的前馈神经网络部分:
NIS框架与前面章节中提到的计算力学存在很多相似之处,NIS可以被视为一种[math]\displaystyle{ \epsilon - machine }[/math],所有历史过程构成的集合[math]\displaystyle{ \overleftarrow{S} }[/math]可以看作是微观状态,所有[math]\displaystyle{ R \in \mathcal{R} }[/math]表示宏观状态,函数[math]\displaystyle{ \eta }[/math]可以理解为一种粗粒化函数,[math]\displaystyle{ \epsilon }[/math]可以理解为一种有效的粗粒化策略,[math]\displaystyle{ T }[/math] 对应于有效的宏观动力学。最小随机性特征表征了宏观动力学的确定性,在因果涌现中可以用有效信息衡量。当整个框架训练足够充分的时候,可以精确地预测未来的微观状态时,编码的宏观状态收敛到有效状态,而有效状态可以被视为计算力学中的因果态。
同时NIS方法与前面提到的G-emergence也有相似之处,例如,NIS同样采用了格兰杰因果的思想:通过预测下一个时间步的微观状态来优化有效的宏观状态。然而,这两个框架之间有几个明显的区别:a)在G-emergence理论中,宏观状态需要人工选择,然后NIS中是通过自动优化粗粒化策略来得到宏观状态;b)NIS使用神经网络来预测未来状态,而G-emergence使用自回归技术来拟合数据。
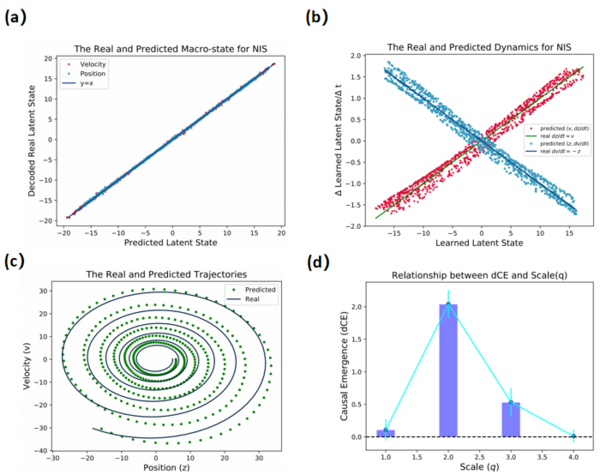
作者在弹簧振子模型中进行了实验,如下图所示,图a展示下一时刻通过编码的结果与通过宏观动力学的迭代结果线性重合验证了模型的有效性,图b展示了学习到的两个动力学和真实的动力学同样线性重合,进一步验证了模型的有效性,图c是模型多步预测的效果,预测和真实的曲线很接近,图d展示了不同尺度下的因果涌现大小,发现在尺度为2时因果涌现最显著,对应了真实的弹簧振子模型也只需要两个状态(位置和速度)就可以描述整个系统。
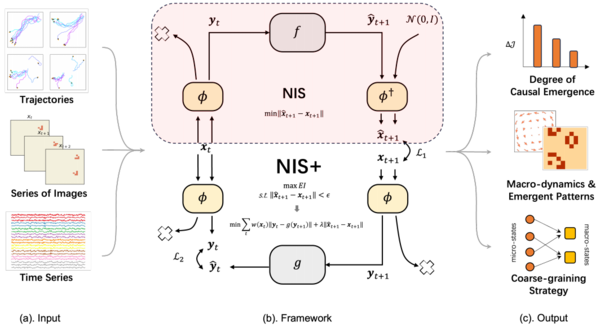
但是该方法存在一些不足,作者将优化过程分为两个阶段,但是没有真正的最大化有效信息。因此,杨等人[38]进一步改进该方法,通过引入反向动力学以及重加权技术借助变分不等式将原始的最大化有效信息转换成最大化其变分下界来直接优化目标函数。目标函数可以被定义为在给定微观预测足够小的情况下最大化宏观动力学的有效信息:
-
[math]\displaystyle{ \begin{aligned}&\max_{\phi,f_{q},\phi^{\dagger}}\mathcal{J}(f_{q}),\\&s.t.\begin{cases}\parallel\hat{x}_{t+1}-x_{t+1}\parallel\lt \epsilon,\\\hat{x}_{t+1}=\phi^{\dagger}\left(f_{q}(\phi(x_{t})\bigr)\right).\end{cases}\end{aligned} }[/math]
(1)
将最大化问题转化为带有约束的最小化问题:
[math]\displaystyle{ \min_{\omega,\theta,\theta'} \sum_{i=0}^{T-1}w(\boldsymbol{x}_t)||\boldsymbol{y}_t-g_{\theta'}(\boldsymbol{y}_{t+1})||+\lambda|| \hat{\boldsymbol{x}}_{t+1}-\boldsymbol{x}_{t+1} || }[/math]
其中[math]\displaystyle{ g }[/math]是反向动力学,[math]\displaystyle{ w(x_t) }[/math]为逆概率权值,如下所示:
[math]\displaystyle{ w(\boldsymbol{x}_t)=\frac{\tilde{p}(\boldsymbol{y}_t)}{p(\boldsymbol{y}_t)}=\frac{\tilde{p}(\phi(\boldsymbol{x}_t))}{p(\phi(\boldsymbol{x}_t))} }[/math]
文章对不同的动力学系统进行了实验,包括SIR动力学、Boids模型、生命游戏以及脑神经系统模型,这里我们选择鸟群和脑实验进行分析。
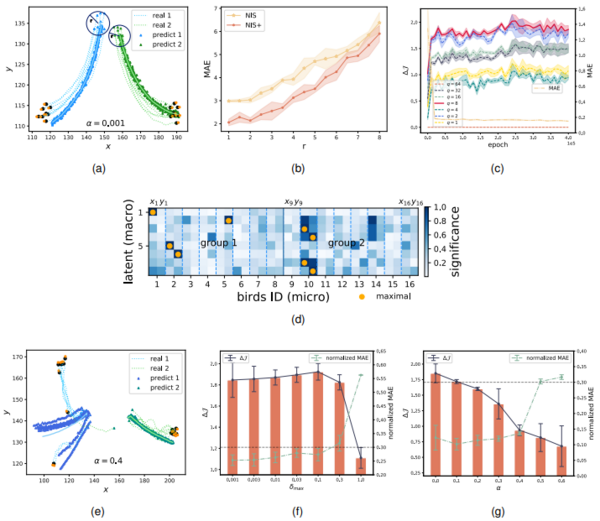
下图为NIS+学习Boids模型的群集行为的实验结果。(a)和(e)给出了不同条件下鸟群的实际和预测轨迹。具体来说,作者将鸟群分为两个组,并且比较了在不同内在噪声水平([math]\displaystyle{ \alpha }[/math]分别为0.001和0.4)下的多步预测结果,在噪音比较小时预测很好,在噪音比较大时预测曲线会发散。(b)展示了多步预测的平均绝对误差(MAE)随着半径r的增加而逐渐上升。(c)展示了不同尺度(q)下的[math]\displaystyle{ \Delta J }[/math]与预测误差(MAE)随着训练epoch的变化,发现在q=8时因果涌现最显著。(d)为归因显著性图,直观地描述了每个宏观维度与每只鸟的空间坐标之间的关联。这里用橙色点突出了每个宏观状态维度中最重要值所对应的微观状态,这些值是使用模型的积分梯度(IG)方法确定的。横轴表示16个物体在微观状态下的x和y坐标,纵轴表示8个宏观维度。淡蓝色的虚线区分了不同个体的坐标,而蓝色实线分隔了两个鸟群。(f)和(g)表示不同噪声水平下[math]\displaystyle{ \Delta J }[/math]和归一化MAE的变化,(f)表示外部噪声的变化(即观测噪音加入到微观数据), (g)表示内在噪声(用[math]\displaystyle{ \alpha }[/math]表示,通过修改Boids模型的动力学加入)。在(f)和(g)中,水平线表示违反误差约束的阈值。当归一化MAE大于阈值0.3时,违反约束,结果不可靠。
NIS+可以通过最大化EI来学习宏观状态和粗粒化策略。这种最大化增强了模型对超出训练数据范围情况的泛化能力。学习到的宏观状态有效地识别了平均群体行为,并且可以使用IG方法将其归因于个体位置。此外,CE的程度随外在噪声的增加而增加,而随内在噪声的减少而减少。这一观察结果表明,通过粗粒化可以消除外在噪声,而内在噪声则不能。
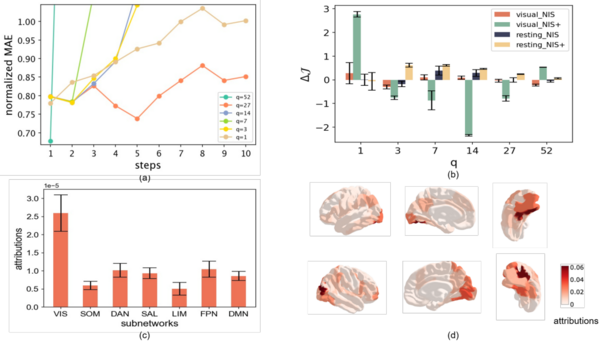
脑实验基于FMRI数据,选择人的静息态和看电影视觉任务,由于原始维度比较高,首先通过使用Schaefer atlas方法对原始的14000维数据降维到100个脑区,构建了6个尺度动力学,图a展示了不同尺度下的多步预测误差,图b展示了在静息态和看电影视觉任务中NIS与NIS+方法的对比,在视觉任务数据中发现scale=1时因果涌现最显著,通过归因分析发现视觉区发挥的作用最大(图c),与真实的场景保持一致,图d展示了脑区归因的不同视角图。
应用
主要讲解因果涌现的潜在应用, 包括: 生物系统、神经网络、脑神经系统、人工智能(因果表示学习、基于世界模型的强化学习)等。
这些定量的量化因果涌现的方法已经广泛应用到很多复杂系统中,包括具有成百上千节点的复杂网络以及神经网络,到具有明显涌现现象的生命游戏、鸟群模型、蛋白质交互、生物以及真实的大脑网络等。
复杂网络中的因果涌现
2020年,Klein和Hoel改进此前提出的基于粗粒化的方法并将其应用到复杂网络中[45],作者借助随机游走子来定义网络中的马尔科夫链,将随机游走子放在节点上等价于对节点做干预,然后基于随机游走概率定义节点的转移概率矩阵。同时作者将有效信息与网络的连通性建立联系,网络中的连通性可以通过节点的出边和入边的权重的不确定性来表征,基于此定义复杂网络中的有效信息。
在随机网络(ER)、偏好依赖网络(PA)等人工网络以及四类真实网络中进行实验比较。对于ER网络来说,有效信息的大小只依赖于连接概率[math]\displaystyle{ p }[/math],并且随着网络规模的增大会收敛到[math]\displaystyle{ -log_2p }[/math]。同时一个关键发现表明,存在一个相变点,该相变点近似在网络的平均度([math]\displaystyle{ \lt k\gt }[/math])等于[math]\displaystyle{ log_2N }[/math]的位置,同样对应于ER网络随着连接概率增加而出现巨连通集团的相变点位置,超过该相变点随机网络结构不会随着其规模的增加而包含更多的信息。对于PA网络来说,[math]\displaystyle{ \alpha\lt 1.0 }[/math]时,有效信息的大小会随着网络规模的增加而增大;[math]\displaystyle{ \alpha\gt 1.0 }[/math]时,结论相反;[math]\displaystyle{ \alpha=1.0 }[/math]对应的无标度网络则是增长的临界边界。对于真实网络,作者发现,生物网络因为具有很大的噪音,所以有效信息最低,通过有效的粗粒化能去除这些噪音,相比于其他类型网络因果涌现最显著,而技术类型网络是更稀疏、非退化的,因此,平均效率更高,节点关系也更加具体,所有有效信息也最高。
在该文章中作者使用贪婪算法来构建宏观尺度的网络,然而对于大规模网络来说,效率仍然很低。随后,Griebenow等[46]提出了一种基于谱聚类的方法来识别偏好依附网络中的因果涌现。相比贪婪算法以及梯度下降算法,谱聚类算法的计算时间最少,同时找到的宏观网络的因果涌现也更加显著。
在生物系统上的应用
生物网络中充满噪音使得很难理解其内部的运作原理,这种噪音一方面来自系统的固有噪音,另一方面是由于测量或观察引入的, Klein等[47]进一步探索了生物网络中的噪声、简并性和确定性三者之间的关系以及具体含义。例如,基因表达网络中的高度确定性关系可以理解为一个基因几乎肯定会导致另一个基因的表达。同时生物系统在进化过程中也普遍存在简并现象,这两个原因导致目前尚不清楚在何种尺度上分析生物系统才能最好地理解它们的功能。Klein等[48]分析了超过1800个物种的蛋白质相互作用网络,发现宏观尺度的网络具有更小的噪音和简并性,同时与不参与宏观尺度的节点相比,组成宏观尺度交互群中的节点更具有弹性。因此,生物网络为了适应进化的要求,需要演化成宏观尺度以提高确定性来增强网络弹性以及提高信息传输的有效性。
Hoel等[49]借助有效信息理论进一步研究生物系统中的因果涌现,作者将有效信息应用到基因调控网络中,识别最能提供信息的心脏发育模型从而控制哺乳动物的心脏发育。通过量化酿酒酵母基因网络的最大联通集团的因果涌现,揭示富有信息的宏观尺度在生物学中是普遍存在的以及生命机制本身也经常运行在宏观尺度上。该方法也为生物学家提供一个可计算的工具来识别最具有信息的宏观尺度,并且可以在此基础上建模、预测、控制和理解复杂的生物系统。
Swain等[50]探索蚁群的交互历史对任务分配和任务切换的影响,使用有效信息研究噪声信息如何在蚂蚁之间进行传播。结果发现,蚁群之间历史交互程度影响任务的分配,并且具体交互中蚂蚁群体的类型决定交互中的噪音。此外,即使当蚂蚁切换功能群时,蚁群涌现出来的凝聚力也能保证群体的稳定,同时不同功能蚁群在维持蚁群凝聚力方面也发挥着不同的作用。
在人工神经网络上的应用
在人工神经网络上的应用,Marrow等[51]尝试引入一个基于信息论的指标即有效信息来量化和跟踪训练过程中DNN因果结构的变化,其中有效信息用于评估节点和边对每层下游目标的因果的影响程度。有效信息可以分解为灵敏性和简并性,通过观察模型训练过程中有效信息,包括灵敏性和简并性的变化就可以确定模型的泛化能力,从而帮助学者更好的理解和解释DNN的工作原理。
在脑神经系统上的应用
脑神经系统是一个涌现的多尺度复杂系统,Luppi等人[52],基于整合信息分解揭示人类意识的协同工作空间,作者构建了脑认知的三层架构,包括:外部环境、具体的模块以及协同全局空间。大脑的工作原理主要包括三个阶段,第一个阶段负责将来自多个不同模块的信息收集到工作空间中,第二个阶段负责在工作空间中整合收集到的信息,第三个阶段负责将全局信息广播到大脑的其他部分。作者在三类不同静息态的FMRI数据上进行实验,包括100个正常人、15个被试者(包括麻醉前、麻醉以及恢复三种不同状态)以及22个慢性意识障碍 (DOC)的被试者,论文方法使用整合信息分解得到协同信息和冗余信息,以及使用修正后的整合信息值[math]\displaystyle{ \Phi_R }[/math],通过计算每两个脑区之间的协同和冗余值可以得到每个脑区发挥更大作用的信息,同时对比有意识人的数据,发现无意识人的整合信息发生显著降低的区域都属于协同信息发挥更大作用的脑区,同时发现整合信息显著降低的区域都属于DMN这样的功能区,从而定位到对于发生意识具有显著作用的脑区。
在人工智能系统上的应用
因果表示学习
因果表示学习是人工智能中的一个新兴领域,它试图将机器学习中的两个重要领域:表示学习和因果推断结合起来。尝试结合两个子领域的优势,自动提取数据背后的重要特征和因果关系[53]。基于粗粒化的因果涌现识别可以等价于一种因果表示学习任务。从数据中识别因果关系的涌现,等价于学习数据背后的潜在因果关系。具体来说,宏观状态可以看成因果变量,动力学学习器类比因果机制,粗粒化策略可以看作是一个从原始数据到因果表示的编码过程,有效信息可以理解为对机制的因果效应强度的衡量。由于这两者存在很多相似之处,使得两个领域的技术和概念可以相互学习。例如,因果表征学习技术可以应用于识别因果涌现,反过来,学习到的抽象因果表征可以被解释为一种宏观状态,从而增加因果表征学习的可解释性。但是两者也存在一些差异,主要包括两点:1)因果表示学习假设其背后存在一个真实的因果机制,数据是由这个因果机制产生的,然而宏观层面涌现出的状态和动力学之间可能并不存在“真正的因果关系”;2)因果涌现中的粗粒化后的宏观状态是一种低维的描述,然而因果表示学习中没有这个要求。但是,从认识论的视角看,两者并不存在差异,因为两者所做的都是从观察数据中提取有效信息,从而获得具有因果效应更强的表征。
基于世界模型的强化学习
基于世界模型的强化学习假设其内部存在一个世界模型可以模拟智能体所面对的环境的动力学[54]。世界模型的动力学可以通过智能体与环境的相互作用来学习,该动力学也可以帮助智能体对不确定的环境做出计划和决策。同时为了表示复杂的环境,世界模型一定是对环境的粗粒化描述,一个典型的世界模型架构总是包含一个编码器和一个解码器。因此,基于世界模型的强化学习与因果涌现也存在很多相似之处。世界模型也可以被视为一种宏观动力学,环境中的所有状态可以看作是宏观状态,这些可以看成是压缩后的忽略无关信息的状态,能捕捉环境中最重要的因果特征,以便智能体做出更好的决策。在计划过程中,智能体也可以使用世界模型来模拟真实世界的动力学。因此,两个领域之间的相似性和共同特征可以帮助我们将一个领域的思想和技术借鉴到另一个领域。例如,具有世界模型的智能体可以将复杂系统作为一个整体来进行相互作用,并从相互作用中获得涌现的因果规律,从而更好的帮助我们做因果涌现识别任务。反过来,最大化有效信息技术也可以用于强化学习,使世界模型具有更强的因果特性。
批判
纵观历史,关于因果关系和涌现的本体论和认识论方面一直存在长期争论。
作者在文献中强调[55],文献中的“causation”概念往往是模糊的,应区分为“cause”和“reason”,符合本体论和认识论的因果关系。“cause”指的是充分导致结果的真实原因,而“reason”则仅仅是个人对结果的解释。Reason可能没有真正的cause那么严格,但它确实提供了一定程度的可预测性。同样,关于因果涌现的本质也存在争论。因果涌现是否是一种独立于特定观察者而存在的真实现象?这里强调,对于Hoel的理论,不同的粗粒化策略可以导致不同的宏观动力学机制与不同的因果效应度量结果(EI)。本质上,不同的粗粒化策略可以被视为代表不同的观察者。Hoel的理论通过干预将涌现与因果关系联系起来,以定量的方式引入了因果涌现的概念,Hoel的理论提出了一个区分粗粒化方法的标准,即EI最大化。因此,对于给定的一组马尔科夫动力学,只有使EI最大化的粗粒化策略和相应的宏观动力学才能被认为是客观结果。然而,当存在多种最大化EI的解决方案时,就会出现挑战,引入一定程度的主观性。Dewhurst[56]对Hoel的理论进行了哲学上的澄清,认为它是认识论的,而不是形而上学的。这表明,Hoel的宏观因果关系仅仅是一种基于信息论的因果解释,而不是涉及“真正的因果”。这也引起了对均匀分布假设的关注,因为没有经验基础支持它优于其他分布。Hoel有效信息的计算依赖于两个前提:(1)系统微观动力学;(2)粗粒化方案。然而,在实践中,很少同时满足这两个条件,特别是在观察性研究中,这两个条件都是未知的。这一局限性阻碍了Hoel理论的实际适用性。
同时有人指出,Hoel的理论忽略了对粗粒化方法的约束,某些粗粒化方法可能导致歧义[57]。此外,一些对状态的粗粒化操作和对时间的粗粒化操作的组合并不表现出可交换性,例如假定[math]\displaystyle{ A_{m \times n} }[/math]是对状态进行粗粒化操作(将n个状态合并为m个状态),这里的粗粒化粗粒化策略是使得宏观状态转移矩阵有效信息最大的策略,[math]\displaystyle{ (\cdot) \times (\cdot) }[/math] 是时间粗粒化操作(将两个时间步骤合并为一个),其中等式[math]\displaystyle{ A_{m\times n}(TPM_{n \times n}) \times A_{m \times n}(TPM_{n \times n}) = A_{m \times n}(TPM_{n \times n} \times TPM_{n \times n}) }[/math]不总是成立。这表明某些粗粒化操作会导致宏观状态的演化与微观系统粗粒化状态的演化存在差异。这意味着需要对粗粒化策略进行一致的约束。下面展示一个具体例子,微观存在3个状态,会发现该马尔科夫矩阵不满足可交换性。
机器学习技术促进了因果结构和模型的学习,以及对涌现属性和因果关系的探索,但重要的是通过机器学习获得的结果是否反映了本体论的因果关系和涌现,或者它们仅仅是认识论现象?尽管机器学习的结合不能解决围绕本体论和认识论因果关系和涌现的争论,但它可以提供有助于减轻主观性的客观标准。这是因为机器学习算法努力优化目标函数。因此,机器学习代理可以被视为“客观”的观察者,对因果关系和涌现做出判断。然而,唯一解问题在这一办法中至关重要。机器学习的结果是本体论还是认识论?答案是,结果是认识论的,依赖于机器学习算法。然而,这并不意味着机器学习的所有结果都是无意义的,因为如果学习代理得到了良好的训练,并且定义的数学目标得到了有效的优化,那么结果也可以被认为是客观的和独立于算法的。结合机器学习方法可以帮助建立观察者建模的理论框架,并研究观察者与相应的被观察复杂系统之间的相互作用。
相关领域研究
存在一些相关领域研究与因果涌现理论联系比较紧密,重点介绍与因果科学、因果模型抽象、模型约简、动力学模式分解以及马尔科夫链的简化的区别和联系。
因果科学
因果涌现能够在分布外场景中增强机器学习的性能,EI中引入的do干预捕获了数据生成过程中的因果依赖性,抑制了虚假相关,从而补充了基于关联的机器学习算法,建立了EI与分布外泛化(OOD)的联系。由于EI的通用性,因果涌现可以应用于监督机器学习来评估特征空间X与目标空间Y之间的因果关系强度,从而提高了从原因(特征)到结果(目标)的预测。值得注意的是,对观测值从X到Y的直接拟合足以满足具有i.i.d.假设的常见预测任务,这意味着训练数据和测试数据是独立同分布的。然而,如果样本是从训练分布之外抽取的,就必须学习一个从训练到测试环境的泛化表示空间。由于人们普遍认为因果关系的泛化性优于统计相关性[58],因此,因果涌现理论可以作为表征空间中嵌入因果关系的标准。因果涌现的发生揭示了目标的潜在因果因素,从而产生了一个关于分布外泛化的鲁棒表示空间。因果涌现可能为基于因果理论的OOD泛化提供一个统一的表征度量。EI也可以看作是分布外泛化的基于重加权的去偏技术的一种信息论抽象。此外,我们猜想,分布外泛化可以在最大化EI的同时实现,EI可能会在原始特征抽象的中期阶段达到顶峰,这与OOD泛化的思想一致,即少即是多。理想情况下,当因果涌现发生在EI的峰值处,所有非因果特征被排除,因果特征被揭示,从而产生最具信息量的表示,同时保持分布变化不变。
因果模型抽象
在复杂系统中,由于微观状态往往存在噪音,需要将微观状态进行粗粒化得到噪音更小的宏观状态,使得宏观动力学的因果性更强。同样对于因果模型也一样,由于原始模型过于复杂,或者计算资源受限,所以往往需要得到更加抽象的因果模型,并且保证抽象的模型尽可能保持原始模型的因果机制,因果模型抽象讨论的也是因果关系与模型抽象(可以看成粗粒化过程)之间的相互作用[59]。因此,因果涌现识别与因果模型抽象有很多相似之处,可以把原始的因果机制理解为微观动力学,抽象出来的机制理解为宏观动力学。在神经信息压缩框架中(NIS),对粗粒化策略和宏观动力学进行了限制,要求宏观动力学的微观预测误差要足够小以排除平凡解。这个要求也类似于因果模型抽象中希望抽象后的因果模型与原始模型的距离要尽可能相近。但是两者也存在一些不同:1)因果涌现中是对状态或数据进行粗粒化,而因果模型抽象是对模型进行操作;2)因果模型抽象中考虑混肴因子,然而却被因果涌现的讨论忽略。
模型约简
因果涌现的一个重要的指标就是粗粒化策略的制定,而粗粒化策略在控制论中有一个非常接近的操作,就是模型约简,Antoulas就曾经写过相关的综述[60]。
模型约简,就是要将高维的复杂系统动力学模型进行化简、降维,用低维的动力学来描述动力系统的演化规律,这一过程其实就是因果涌现研究中的粗粒化过程。将对大尺度动力系统的近似方法主要有两大类,即基于奇异值分解[60][61]的近似方法和基于Krylov[60][62][63]的近似方法。前者基于奇异值分解,后者基于矩匹配。虽然前者具有许多理想的性质,包括误差界,但它不能应用于高复杂度的系统。另一方面,后者的优势在于它可以迭代实现,因此适用于高复杂度系统。将这两个族的最佳属性相结合的努力导致了第三类近似方法,称为SVD/Krylov[64][65]。两种方法都是基于粗粒化前后输出函数的误差损失函数,而目标就是寻找能使误差最小的约简参数矩阵[math]\displaystyle{ W }[/math]。
一般情况下基于模型约简前后输出函数的误差损失函数[math]\displaystyle{ ||\hat{z}-z|| }[/math]判断粗粒化参数默认了系统约简的过程会损失信息量,因此误差最小化是判断约简方法有效性的唯一方法。但是如果从因果涌现角度考虑,有效信息会因为降维而增大,这也是因果涌现研究中的粗粒化策略和控制论中的模型约简最大的不同。当动力系统是随机的时候[66],直接计算损失函数会因为随机性的存在,导致损失函数的稳定性无法保证,因而约简的有效性也会无法准确测量。而本身就是基于随机动力系统的有效信息和因果涌现指标,一定程度上可以增加评判指标的有效性,使对随机动力系统的控制研究更加严谨。
动力学模式分解
动态模态分解[67][68]模型的基本思想是直接从数据模拟得到的流场中提取流动的动态信息,根据不同频率的流场变动寻找数据映射,基于动态非线性无穷维转化成动态线性有穷维的方式,采用了Arnoldi 方法以及奇异值分解SVD降维的思想,借鉴了ARIMA、SARIMA 以及季节模型等许多时间序列的关键特征,被广泛的使用在数学、物理、金融等领域[69]。动态模式分解按照频率对系统进行排序,提取系统特征频率,从而观察不同频率的流动结构对流场的贡献,同时动态模式分解模态特征值可以进行流场预测。因为动态模态分解算法只理论的严密性、稳定性、简易性等优点,在不断被运用的同时,动态模态分解算法也在本来的基础之上不断被完善,如与SPA检验结合起来,以验证股票价格预测对比基准点的强有效性:以及通过联系动态模态分解算法和光谱研究的方式,模拟股票市场在循环经济当中的震动,均能够有效地采集分析数据,并最终得到结果。
动力学模式分解,属于利用线性变换同时对变量、动力学、观测函数进行降维[70]。而除此之外,还有另一种和因果涌现中粗粒化策略相近,但是依然基于误差最小化来进行优化的操作,就是动力学模式分解。模型约简和动力学模式分解虽然都和模型粗粒化十分接近,但是他们都没有基于有效信息的优化,本质上都是默认了一定会损失信息,而不会增强因果效应。后续的证明[71]中我们知道其实有效信息最大化的最优解集包含因果涌最大化的解集,因此如果要优化因果涌现,可以先最小化误差,在最小误差的解集中寻找最佳的粗粒化策略。
马尔科夫链的简化
除了对向量以及高维动力学的降维之外,马尔科夫链的简化也和因果涌现有着重要的联系。马尔科夫链的简化,其实就是对复杂的马尔科夫链进行分块与重整。而分块的重要依据就是马尔科夫链是否可约[72]。
可约马尔可夫链描述的系统具有特定状态,一旦我们访问了其中一种状态,就无法访问其他状态。可以用可约马尔可夫链建模的系统的一个例子是赌博游戏,一旦赌徒破产,游戏就会停止。更形象的一个例子是研究一条鱼在海洋中游动的位置。鱼可以自由地游动到任何位置,这取决于水流、食物或捕食者的存在。一旦鱼被网住,它就无法逃脱,因此它能游动的空间也是有限的。
但如果从任何状态开始,我们都能够直接、一步或间接地通过一个或多个中间状态到达图中的任何其他状态,这样的马尔可夫链就称为不可约马尔可夫链。在可以长时间运行的系统中,我们会遇到不可约马尔可夫链,例如银行营业时间内的排队状态,排队的顾客数量一直在零到最大值之间变化。或是路由器或交换机中的缓冲区占用状态。缓冲区占用根据到达的流量模式在完全空和完全满之间变化。从任何状态开始,我们都可能无法直接或间接地到达图中的其他状态。这种马尔可夫链被称为可约马尔可夫。
对马尔科夫概率转移矩阵实施粗粒化的方法,其实就利用了马尔科夫链的可约性与不可约性。关于具体的粗粒化马尔科夫链的方法,请参考马尔科夫链的粗粒化。
例如
| [math]\displaystyle{ P_m=\begin{pmatrix} &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &0 &1 &0 &1& \\ \end{pmatrix} }[/math], |
前三个状态之间可以相互转化,因此前三个节点这部分就是不可约的,而前三个节点无论如何无法进入第四个节点,反之亦然,因此整个马尔科夫链就是可约的,我们可以将前三个节点组成一个整体,生成宏观态,我们也可以把因果涌现作为指标,评判马尔科夫链的简化是否最佳。
参考文献
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Hoel E P, Albantakis L, Tononi G. Quantifying causal emergence shows that macro can beat micro[J]. Proceedings of the National Academy of Sciences, 2013, 110(49): 19790-19795.
- ↑ 2.0 2.1 2.2 2.3 2.4 Hoel E P. When the map is better than the territory[J]. Entropy, 2017, 19(5): 188.
- ↑ Meehl P E, Sellars W. The concept of emergence[J]. Minnesota studies in the philosophy of science, 1956, 1239-252.
- ↑ 4.0 4.1 Holland J H. Emergence: From chaos to order[M]. OUP Oxford, 2000.
- ↑ Anderson P W. More is different: broken symmetry and the nature of the hierarchical structure of science[J]. Science, 1972, 177(4047): 393-396.
- ↑ Holland, J.H. Hidden Order: How Adaptation Builds Complexity; Addison Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1996.
- ↑ Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 27–31 July 1987; pp. 25–34.
- ↑ Wei, J.; Tay, Y.; Bommasani, R.; Raffel, C.; Zoph, B.; Borgeaud, S.; Yogatama, D.; Bosma, M.; Zhou, D.; Metzler, D.; et al. Emergent abilities of large language models. arXiv 2022, arXiv:2206.07682.
- ↑ 9.0 9.1 Bedau, M.A. Weak emergence. Philos. Perspect. 1997, 11, 375–399. [CrossRef]
- ↑ Bedau, M. Downward causation and the autonomy of weak emergence. Principia Int. J. Epistemol. 2002, 6, 5–50.
- ↑ 11.0 11.1 Harré, R. The Philosophies of Science; Oxford University Press: New York, NY, USA , 1985.
- ↑ 12.0 12.1 Baas, N.A. Emergence, hierarchies, and hyperstructures. In Artificial Life III, SFI Studies in the Science of Complexity, XVII; Routledge: Abingdon, UK, 1994; pp. 515–537.
- ↑ Newman, D.V. Emergence and strange attractors. Philos. Sci. 1996, 63, 245–261. [CrossRef]
- ↑ 14.0 14.1 Kim, J. ‘Downward causation’ in emergentism and nonreductive physicalism. In Emergence or Reduction; Walter de Gruyter: Berlin, Germany, 1992; pp. 119–138.
- ↑ 15.0 15.1 O’Connor, T. Emergent properties. Am. Philos. Q. 1994, 31, 91–104
- ↑ Fromm, J. Types and forms of emergence. arXiv 2005, arXiv:nlin/0506028
- ↑ Bedau, M.A.; Humphreys, P. Emergence: Contemporary Readings in Philosophy and Science; MIT Press: Cambridge, MA, USA, 2008.
- ↑ Yurchenko, S.B. Can there be a synergistic core emerging in the brain hierarchy to control neural activity by downward causation? TechRxiv 2023 . [CrossRef]
- ↑ 19.0 19.1 Pearl J. Causality[M]. Cambridge university press, 2009.
- ↑ Granger C W. Investigating causal relations by econometric models and cross-spectral methods[J]. Econometrica: journal of the Econometric Society, 1969, 424-438.
- ↑ 21.0 21.1 Pearl J. Models, reasoning and inference[J]. Cambridge, UK: CambridgeUniversityPress, 2000, 19(2).
- ↑ Spirtes, P.; Glymour, C.; Scheines, R. Causation Prediction and Search, 2nd ed.; MIT Press: Cambridge, MA, USA, 2000.
- ↑ Chickering, D.M. Learning equivalence classes of Bayesian-network structures. J. Mach. Learn. Res. 2002, 2, 445–498.
- ↑ Eells, E. Probabilistic Causality; Cambridge University Press: Cambridge, UK, 1991; Volume 1
- ↑ Suppes, P. A probabilistic theory of causality. Br. J. Philos. Sci. 1973, 24, 409–410.
- ↑ 26.0 26.1 26.2 26.3 26.4 Zhang J, Tao R, Yuan B. Dynamical Reversibility and A New Theory of Causal Emergence. arXiv preprint arXiv:2402.15054. 2024 Feb 23.
- ↑ 27.0 27.1 J. P. Crutchfield, K. Young, Inferring statistical complexity, Physical review letters 63 (2) (1989) 105.
- ↑ 28.0 28.1 A. K. Seth, Measuring emergence via nonlinear granger causality., in: alife, Vol. 2008, 2008, pp. 545–552.
- ↑ C. R. Shalizi, C. Moore, What is a macrostate? subjective observations and objective dynamics, arXiv preprint cond-mat/0303625 (2003).
- ↑ Mnif, M.; Müller-Schloer, C. Quantitative emergence. In Organic Computing—A Paradigm Shift for Complex Systems; Springer: Basel, Switzerland, 2011; pp. 39–52.
- ↑ Fisch, D.; Jänicke, M.; Sick, B.; Müller-Schloer, C. Quantitative emergence–A refined approach based on divergence measures. In Proceedings of the 2010 Fourth IEEE International Conference on Self-Adaptive and Self-Organizing Systems, Budapest, Hungary, 27 September–1 October 2010; IEEE Computer Society: Washington, DC, USA, 2010; pp. 94–103.
- ↑ Fisch, D.; Fisch, D.; Jänicke, M.; Kalkowski, E.; Sick, B. Techniques for knowledge acquisition in dynamically changing environments. ACM Trans. Auton. Adapt. Syst. (TAAS) 2012, 7, 1–25. [CrossRef]
- ↑ Holzer, R.; De Meer, H.; Bettstetter, C. On autonomy and emergence in self-organizing systems. In International Workshop on Self-Organizing Systems, Proceedings of the Third International Workshop, IWSOS 2008, Vienna, Austria, 10–12 December 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 157–169.
- ↑ Holzer, R.; de Meer, H. Methods for approximations of quantitative measures in self-organizing systems. In Proceedings of the Self-Organizing Systems: 5th International Workshop, IWSOS 2011, Karlsruhe, Germany, 23–24 February 2011; Proceedings 5; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–15.
- ↑ Teo, Y.M.; Luong, B.L.; Szabo, C. Formalization of emergence in multi-agent systems. In Proceedings of the 1st ACM SIGSIM Conference on Principles of Advanced Discrete Simulation, Montreal, QC, Canada, 19–22 May 2013; pp. 231–240.
- ↑ Szabo, C.; Teo, Y.M. Formalization of weak emergence in multiagent systems. ACM Trans. Model. Comput. Simul. (TOMACS) 2015, 26, 1–25. [CrossRef]
- ↑ 37.0 37.1 37.2 37.3 Rosas F E, Mediano P A, Jensen H J, et al. Reconciling emergences: An information-theoretic approach to identify causal emergence in multivariate data[J]. PLoS computational biology, 2020, 16(12): e1008289.
- ↑ 38.0 38.1 38.2 Barnett L, Seth AK. Dynamical independence: discovering emergent macroscopic processes in complex dynamical systems. Physical Review E. 2023 Jul;108(1):014304.
- ↑ Tononi G, Sporns O. Measuring information integration[J]. BMC neuroscience, 2003, 41-20.
- ↑ Chvykov P; Hoel E. (2021). "Causal Geometry". Entropy. 23 (1): 24.
- ↑ Liu K; Yuan B; Zhang J (2024). "An Exact Theory of Causal Emergence for Linear Stochastic Iteration Systems". Entropy. 26 (8): 618.
- ↑ Williams P L, Beer R D. Nonnegative decomposition of multivariate information[J]. arXiv preprint arXiv:10042515, 2010.
- ↑ P. A. Mediano, F. Rosas, R. L. Carhart-Harris, A. K. Seth, A. B. Barrett, Beyond integrated information: A taxonomy of information dynamics phenomena, arXiv preprint arXiv:1909.02297 (2019).
- ↑ Zhang J, Liu K. Neural information squeezer for causal emergence[J]. Entropy, 2022, 25(1): 26.
- ↑ Klein B, Hoel E. The emergence of informative higher scales in complex networks[J]. Complexity, 2020, 20201-12.
- ↑ Griebenow R, Klein B, Hoel E. Finding the right scale of a network: efficient identification of causal emergence through spectral clustering[J]. arXiv preprint arXiv:190807565, 2019.
- ↑ Klein B, Swain A, Byrum T, et al. Exploring noise, degeneracy and determinism in biological networks with the einet package[J]. Methods in Ecology and Evolution, 2022, 13(4): 799-804.
- ↑ Klein B, Hoel E, Swain A, et al. Evolution and emergence: higher order information structure in protein interactomes across the tree of life[J]. Integrative Biology, 2021, 13(12): 283-294.
- ↑ Hoel E, Levin M. Emergence of informative higher scales in biological systems: a computational toolkit for optimal prediction and control[J]. Communicative & Integrative Biology, 2020, 13(1): 108-118.
- ↑ Swain A, Williams S D, Di Felice L J, et al. Interactions and information: exploring task allocation in ant colonies using network analysis[J]. Animal Behaviour, 2022, 18969-81.
- ↑ Marrow S, Michaud E J, Hoel E. Examining the Causal Structures of Deep Neural Networks Using Information Theory[J]. Entropy, 2020, 22(12): 1429.
- ↑ Luppi AI, Mediano PA, Rosas FE, Allanson J, Pickard JD, Carhart-Harris RL, Williams GB, Craig MM, Finoia P, Owen AM, Naci L. A synergistic workspace for human consciousness revealed by integrated information decomposition. BioRxiv. 2020 Nov 26:2020-11.
- ↑ B. Sch ̈olkopf, F. Locatello, S. Bauer, N. R. Ke, N. Kalchbrenner, A. Goyal, Y. Bengio, Toward causal representation learning, Proceedings of the IEEE 109 (5) (2021) 612–634.
- ↑ D. Ha, J. Schmidhuber, World models, arXiv preprint arXiv:1803.10122 (2018).
- ↑ Yurchenko, S. B. (2023). Can there be a synergistic core emerging in the brain hierarchy to control neural activity by downward causation?. Authorea Preprints.
- ↑ Dewhurst, J. (2021). Causal emergence from effective information: Neither causal nor emergent?. Thought: A Journal of Philosophy, 10(3), 158-168.
- ↑ Eberhardt, F., & Lee, L. L. (2022). Causal emergence: When distortions in a map obscure the territory. Philosophies, 7(2), 30.
- ↑ Arjovsky, M.; Bottou, L.; Gulrajani, I.; Lopez-Paz, D. Invariant risk minimization. arXiv 2019, arXiv:1907.02893.
- ↑ S. Beckers, F. Eberhardt, J. Y. Halpern, Approximate causal abstractions, in: Uncertainty in artificial intelligence, PMLR, 2020, pp. 606–615.
- ↑ 60.0 60.1 60.2 Antoulas A C. An overview of approximation methods for large-scale dynamical systems[J]. Annual reviews in Control, 2005, 29(2): 181-190.
- ↑ Gallivan K, Grimme E, Van Dooren P. Asymptotic waveform evaluation via a Lanczos method[J]. Applied Mathematics Letters, 1994, 7(5): 75-80.
- ↑ CHRISTIAN DE VILLEMAGNE & ROBERT E. SKELTON (1987) Model reductions using a projection formulation, International Journal of Control, 46:6, 2141-2169, DOI: 10.1080/00207178708934040
- ↑ Boley D L. Krylov space methods on state-space control models[J]. Circuits, Systems and Signal Processing, 1994, 13: 733-758.
- ↑ Gugercin S. An iterative SVD-Krylov based method for model reduction of large-scale dynamical systems[J]. Linear Algebra and its Applications, 2008, 428(8-9): 1964-1986.
- ↑ Khatibi M, Zargarzadeh H, Barzegaran M. Power system dynamic model reduction by means of an iterative SVD-Krylov model reduction method[C]//2016 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT). IEEE, 2016: 1-6.
- ↑ CHRISTIAN DE VILLEMAGNE & ROBERT E. SKELTON (1987) Model reductions using a projection formulation, International Journal of Control, 46:6, 2141-2169, DOI: 10.1080/00207178708934040
- ↑ Schmid P J. Dynamic mode decomposition and its variants[J]. Annual Review of Fluid Mechanics, 2022, 54(1): 225-254.
- ↑ J. Proctor, S. Brunton and J. N. Kutz, Dynamic mode decomposition with control, arXiv:1409.6358
- ↑ J. Grosek and J. N. Kutz, Dynamic mode decomposition for real-time background/foreground separation in video, arXiv:1404.7592.
- ↑ B. Brunton, L. Johnson, J. Ojemann and J. N. Kutz, Extracting spatial-temporal coherent patterns in large-scale neural recordings using dynamic mode decomposition arXiv:1409.5496
- ↑
Liu K, Yuan B, Zhang J. An Exact Theory of Causal Emergence for Linear Stochastic Iteration Systems[J]. arXiv preprint arXiv:2405.09207, 2024.
- ↑ Gebali F, Gebali F. Reducible Markov Chains[J]. Analysis of Computer Networks, 2015: 157-189.
编者推荐
下面是一些链接能够帮助读者更好的了解因果涌现的相关信息:
因果涌现读书会
分享近期发展起来的一些理论与工具,包括因果涌现理论、机器学习驱动的重整化技术,以及自指动力学正在发展一套跨尺度的分析框架等。
涌现现象无非是复杂系统中诸多现象中最神秘莫测的一个,而Erik Hoel提出的“因果涌现”理论为这种跨层次的奇妙涌现现象提供了一种新的可能解释途径。通过跨层次的粗粒化(Coarse-graining, 或称重整化Renormalization)操作,我们便可以在同一个动力学系统上在不同的尺度得到完全不同的动力学,通过本季读书会梳理,我们希望探讨这一新兴领域的前沿进展,衍生更多新的研究课题。
涌现与因果的结合创造了因果涌现的概念。这是一套利用因果性来定量刻画涌现的理论体系,本季读书会通过阅读前沿文献,加深我们对因果、涌现等概念的理解;聚焦于寻找因果与涌现、多尺度等概念相结合的研究方向;并探索复杂系统多尺度自动建模的研究方向。第二季读书会更加集中在探讨因果科学与因果涌现之间的关系,以及对涌现进行定量刻画,聚焦于寻找因果与涌现、多尺度等概念相结合的研究方向;并探索复杂系统多尺度自动建模的研究方向。
因果涌现第三季的读书会中,将进一步围绕因果涌现的核心研究问题『因果涌现的定义』以及『因果涌现的辨识』来进行深入的学习和讨论,对 Erik Hoel 提出的 Causal Emergence,Causal Geometry 等因果涌现的核心理论进行深入的探讨和剖析,并且详细梳理其中涉及到的方法论,包括从动力学约简、隐空间动力学学习等其他研究领域中学习和借鉴相关的研究思路,最后探讨因果涌现的应用,包括基于生物网络、脑网络或者涌现探测等问题展开扩展,发掘更多的实际应用场景。
文章推荐
- Zhang, J.; Liu, K. Neural Information Squeezer for Causal Emergence. Entropy 2023, 25, 26.
文章提出了一种名为 "神经信息挤压器"(Neural Information Squeezer)的通用机器学习框架,能自动提取有效的粗粒化策略和宏观动力学,并直接从时间序列数据中识别因果涌现。
路径推荐
- 张江老师根据因果涌现读书会第一季梳理的关于因果涌现的学习路径:https://pattern.swarma.org/article/153
此词条由王志鹏编写,张江、王志鹏整理和审校。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。