奇异值分解(SVD)
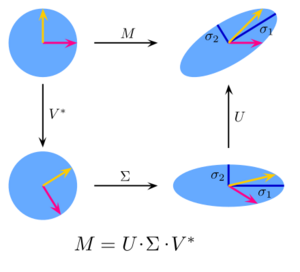
在线性代数中,奇异值分解(Singular value decomposition)是一种通过旋转、缩放和再次旋转来对实矩阵(real matrix 元素都是实数的矩阵)或复矩阵(complex matrix 元素有复数的矩阵)进行因式分解的方法,如下图。它把具有正交特征基(orthonormal eigenbasis)的方阵特征分解(eigen decomposition 矩阵分解为特征向量和特征值)推广到了任意 [math]\displaystyle{ m \times n }[/math] 矩阵,并与极分解(polar decomposition)密切相关。
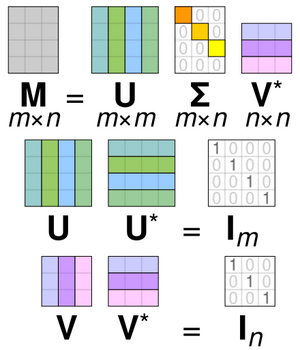
具体而言,我们可以将一个 [math]\displaystyle{ m \times n }[/math] 复矩阵 [math]\displaystyle{ \mathbf{M} }[/math] 分解为 [math]\displaystyle{ \mathbf{M} = \mathbf{U\Sigma V^*} }[/math]。在这里,[math]\displaystyle{ \mathbf{U} }[/math] 是 [math]\displaystyle{ m \times m }[/math] 复酉矩阵(complex unitary matrix 共轭转置为其逆的复数矩阵),[math]\displaystyle{ \mathbf{\Sigma} }[/math] 是 [math]\displaystyle{ m \times n }[/math] 矩形对角矩阵(rectangular diagonal matrix),其对角线元素为非负实数,[math]\displaystyle{ \mathbf{V} }[/math] 是 [math]\displaystyle{ n \times n }[/math] 复酉矩阵,而 [math]\displaystyle{ \mathbf{V}^* }[/math] 是 [math]\displaystyle{ \mathbf{V} }[/math] 的共轭转置(conjugate transpose)。这种分解适用于任何复矩阵。若 [math]\displaystyle{ \mathbf{M} }[/math] 为实矩阵,则 [math]\displaystyle{ \mathbf{U} }[/math] 和 [math]\displaystyle{ \mathbf{V} }[/math] 必为实正交矩阵(real orthogonal matrices);此时,我们通常将SVD表示为 [math]\displaystyle{ \mathbf{M} = \mathbf{U\Sigma V}^{\mathrm{T}} }[/math]。
[math]\displaystyle{ \mathbf{\Sigma} }[/math] 的对角元素 [math]\displaystyle{ \sigma_i = \Sigma_{ii} }[/math] 由 [math]\displaystyle{ \mathbf{M} }[/math] 唯一确定,称为 [math]\displaystyle{ \mathbf{M} }[/math] 的奇异值。非零奇异值的数量等于 [math]\displaystyle{ \mathbf{M} }[/math] 的秩(rank)。我们把 [math]\displaystyle{ \mathbf{U} }[/math] 的列和 [math]\displaystyle{ \mathbf{V} }[/math] 的列分别叫做 [math]\displaystyle{ \mathbf{M} }[/math] 的左奇异向量和右奇异向量。它们分别构成两组标准正交基(orthonormal bases) [math]\displaystyle{ \mathbf{u}_1, \ldots, \mathbf{u}_m }[/math] 和 [math]\displaystyle{ \mathbf{v}_1, \ldots, \mathbf{v}_n }[/math]。如果我们将值为零的奇异值 [math]\displaystyle{ \sigma_i }[/math] 排在最后,奇异值分解就可以写成:
[math]\displaystyle{ \mathbf{M} = \mathbf{U\Sigma V^*} = \sum_{i=1}^r \sigma_i \mathbf{u}_i \mathbf{v}_i^* }[/math]
这里 [math]\displaystyle{ r \leq \min\left \{ m,n \right \} }[/math] 是 [math]\displaystyle{ \mathbf{M} }[/math] 的秩。
虽然SVD不是唯一的,但我们总是可以选择让奇异值 [math]\displaystyle{ \Sigma_{ii} }[/math] 按降序排列。这样一来,[math]\displaystyle{ \mathbf{\Sigma} }[/math](而非 [math]\displaystyle{ \mathbf{U} }[/math] 和 [math]\displaystyle{ \mathbf{V} }[/math])就由 [math]\displaystyle{ \mathbf{M} }[/math] 唯一确定了。
有时,我们也把SVD称为紧凑SVD(compact SVD)。紧凑型SVD是与之类似的一个分解,形如[math]\displaystyle{ \mathbf{M} = \mathbf{U_r\Sigma_r V_r}^* }[/math],其中 [math]\displaystyle{ \mathbf{\Sigma} }[/math] 是 [math]\displaystyle{ r \times r }[/math] 的方形对角矩阵,[math]\displaystyle{ r \leq \min\left \{ m,n \right \} }[/math],[math]\displaystyle{ r }[/math]就是 [math]\displaystyle{ \mathbf{M} }[/math] 的秩,只包含非零奇异值。在这种变体中,[math]\displaystyle{ \mathbf{U} }[/math] 是 [math]\displaystyle{ m \times r }[/math] 半酉矩阵(semi-unitary matrix 非方阵的酉矩阵),[math]\displaystyle{ \mathbf{V} }[/math] 是 [math]\displaystyle{ n \times r }[/math] 半酉矩阵,满足 [math]\displaystyle{ \mathbf{U}^* \mathbf{U} = \mathbf{V}^* \mathbf{V} = \mathbf{I}_r }[/math](单位矩阵)。
SVD在数学上有多种应用,包括计算伪逆(pseudoinverse)、矩阵近似(matrix approximation)以及确定矩阵的秩(rank 线性无关向量的最大个数)、值域(range)和零空间(null space)。此外,SVD在科学、工程和统计学的各个领域都很有用,比如信号处理(signal processing)、数据最小二乘拟合(least squares fitting of data)和过程控制等。
直观解释
旋转、坐标缩放和反射
特殊情况下,当[math]\displaystyle{ \mathbf{M} }[/math]是[math]\displaystyle{ m \times m }[/math]的实方阵时,我们也可以将矩阵[math]\displaystyle{ \mathbf{U} }[/math]和[math]\displaystyle{ \mathbf{V}^* }[/math]选为实[math]\displaystyle{ m \times m }[/math]矩阵。此时,"酉矩阵"和"正交矩阵"实际上是一回事。我们可以将这两个酉矩阵和对角矩阵(这里统称为[math]\displaystyle{ \mathbf{A} }[/math])解读为空间[math]\displaystyle{ \mathbb{R}^m }[/math]的线性变换(linear transformation)[math]\displaystyle{ x \mapsto \mathbf{Ax} }[/math]。其中,矩阵[math]\displaystyle{ \mathbf{U} }[/math]和[math]\displaystyle{ \mathbf{V}^* }[/math]代表空间的旋转(rotations)或反射(reflection),而[math]\displaystyle{ \boldsymbol{\Sigma} }[/math]则表示对每个坐标[math]\displaystyle{ x_i }[/math]按因子[math]\displaystyle{ \sigma_i }[/math]进行的缩放变换(scaling)。这样,奇异值分解就把[math]\displaystyle{ \mathbb{R}^m }[/math]的任何线性变换分解成了三个几何变换的组合:先旋转或反射([math]\displaystyle{ \mathbf{V}^* }[/math]),然后逐坐标缩放([math]\displaystyle{ \boldsymbol{\Sigma} }[/math]),最后再旋转或反射([math]\displaystyle{ \mathbf{U} }[/math])。
特别地,如果[math]\displaystyle{ \mathbf{M} }[/math]的行列式为正,[math]\displaystyle{ \mathbf{U} }[/math]和[math]\displaystyle{ \mathbf{V}^* }[/math]需要同时带反射或同时都不带反射。若行列式为负,则只有一个会带反射。若行列式为零,我们可以随意选择每个矩阵的类型。
当[math]\displaystyle{ \mathbf{M} }[/math]是实矩阵但非方阵,即[math]\displaystyle{ m \times n }[/math]且[math]\displaystyle{ m \neq n }[/math]时(如下图),我们可以将其视为从[math]\displaystyle{ \mathbb{R}^n }[/math]到[math]\displaystyle{ \mathbb{R}^m }[/math]的线性变换。这时,我们可以选择[math]\displaystyle{ \mathbf{U} }[/math]和[math]\displaystyle{ \mathbf{V}^* }[/math]分别为[math]\displaystyle{ \mathbb{R}^m }[/math]和[math]\displaystyle{ \mathbb{R}^n }[/math]的旋转/反射;而[math]\displaystyle{ \boldsymbol{\Sigma} }[/math]除了缩放前[math]\displaystyle{ \min\left\{m,n\right\} }[/math]个坐标外,还会用零扩展向量或删除尾部坐标,从而将[math]\displaystyle{ \mathbb{R}^n }[/math]转换为[math]\displaystyle{ \mathbb{R}^m }[/math]。
奇异值作为椭圆或椭球体的半轴
如下图所示,我们可以将奇异值理解为二维椭圆半轴的长度。这一概念可以推广到[math]\displaystyle{ n }[/math]维欧几里得空间(Euclidean space):任何[math]\displaystyle{ n \times n }[/math]方阵的奇异值都可以看作[math]\displaystyle{ n }[/math]维椭球体半轴的长度。同理,任何[math]\displaystyle{ m \times n }[/math]矩阵的奇异值可以视为[math]\displaystyle{ m }[/math]维空间中[math]\displaystyle{ n }[/math]维椭球体半轴的长度,比如三维空间中(倾斜的)二维平面上的椭圆。奇异值编码了半轴的长度,而奇异向量则编码了方向。详见下文:
[math]\displaystyle{ \mathbf{U} }[/math]和[math]\displaystyle{ \mathbf{V} }[/math]的列构成标准正交基
由于[math]\displaystyle{ \mathbf{U} }[/math]和[math]\displaystyle{ \mathbf{V}^* }[/math]都是酉矩阵,它们的列分别形成一组标准正交向量(orthonormal vectors 模为1且彼此正交的向量),我们可以将其视为基向量(basis vectors 张成向量空间的一组线性无关向量)。矩阵[math]\displaystyle{ \mathbf{M} }[/math]把基向量[math]\displaystyle{ \mathbf{V}_i }[/math]映射到拉伸后的单位向量[math]\displaystyle{ \sigma_i\mathbf{U}_i }[/math]上。根据酉矩阵的定义,它们的共轭转置[math]\displaystyle{ \mathbf{U}^* }[/math]和[math]\displaystyle{ \mathbf{V} }[/math]也具有相同性质,只是失去了奇异值作为拉伸的几何解释。简言之,[math]\displaystyle{ \mathbf{U} }[/math]、[math]\displaystyle{ \mathbf{U}^* }[/math]、[math]\displaystyle{ \mathbf{V} }[/math]和[math]\displaystyle{ \mathbf{V}^* }[/math]的列都构成标准正交基(orthonormal bases 模为1且正交的基向量集合)。
当[math]\displaystyle{ \mathbf{M} }[/math]是半正定厄米矩阵(positive-semidefinite Hermitian matrix)时,[math]\displaystyle{ \mathbf{U} }[/math]和[math]\displaystyle{ \mathbf{V} }[/math]都等同于用于对角化[math]\displaystyle{ \mathbf{M} }[/math]的酉矩阵。然而,如果[math]\displaystyle{ \mathbf{M} }[/math]不是半正定厄米矩阵但仍可对角化的时候,那么其特征分解(矩阵分解为特征值与特征向量)和奇异值分解就会有所不同。
与四个基本子空间的关系:
- [math]\displaystyle{ \mathbf{U} }[/math]的前[math]\displaystyle{ r }[/math]列构成了[math]\displaystyle{ \mathbf{M} }[/math]的列空间(矩阵列向量张成的空间)的基。
- [math]\displaystyle{ \mathbf{U} }[/math]的后[math]\displaystyle{ m-r }[/math]列则构成[math]\displaystyle{ \mathbf{M}^* }[/math]的零空间(矩阵映射中被映射到零的所有向量集合)的基。
- [math]\displaystyle{ \mathbf{V} }[/math]的前[math]\displaystyle{ r }[/math]列构成[math]\displaystyle{ \mathbf{M}^* }[/math]列空间的基(在实数情况下即为[math]\displaystyle{ \mathbf{M} }[/math]的行空间(矩阵行向量张成的空间)的基)。
- [math]\displaystyle{ \mathbf{V} }[/math]的后[math]\displaystyle{ n-r }[/math]列构成[math]\displaystyle{ \mathbf{M} }[/math]的零空间的基。
几何意义:
由于[math]\displaystyle{ \mathbf{U} }[/math]和[math]\displaystyle{ \mathbf{V} }[/math]是酉矩阵,[math]\displaystyle{ \mathbf{U} }[/math]的列[math]\displaystyle{ \mathbf{U}_1,\ldots,\mathbf{U}_m }[/math]构成[math]\displaystyle{ K^m }[/math]的标准正交基,[math]\displaystyle{ \mathbf{V} }[/math]的列[math]\displaystyle{ \mathbf{V}_1,\ldots,\mathbf{V}_n }[/math]构成[math]\displaystyle{ K^n }[/math]的标准正交基(基于这些空间的标量积(scalar products 两个向量间的内积))。
我们可以定义一个线性变换为:
[math]\displaystyle{ T:\left\{{\begin{aligned}K^{n}&\to K^{m}\\x&\mapsto \mathbf{M} x\end{aligned}}\right. }[/math]
则该映射在这些标准正交基下有一个简洁的描述:
[math]\displaystyle{ T(\mathbf{V}_i)=\sigma_i\mathbf{U}_i, \qquad i=1,\ldots,\min(m,n), }[/math]
其中[math]\displaystyle{ \sigma_i }[/math]是[math]\displaystyle{ \mathbf{\Sigma} }[/math]的第[math]\displaystyle{ i }[/math]个对角元素,当[math]\displaystyle{ i\gt \min(m,n) }[/math]时,[math]\displaystyle{ T(\mathbf{V}_i)=0 }[/math]。
所谓的SVD定理的几何含义可以概括为:对于每个线性映射[math]\displaystyle{ T:K^n\to K^m }[/math],我们能找到[math]\displaystyle{ K^n }[/math]和[math]\displaystyle{ K^m }[/math]的标准正交基,使[math]\displaystyle{ T }[/math]将[math]\displaystyle{ K^n }[/math]的第[math]\displaystyle{ i }[/math]个基向量映射到[math]\displaystyle{ K^m }[/math]的第[math]\displaystyle{ i }[/math]个基向量的非负倍数,并将剩余基向量映射到零。在这些基下,映射[math]\displaystyle{ T }[/math]表现为一个具有非负实数对角元素的对角矩阵。
为了更直观地理解奇异值和SVD分解(至少在实向量空间中),我们可以考虑[math]\displaystyle{ \mathbf{R}^n }[/math]中半径为1的球面[math]\displaystyle{ S }[/math]。线性映射[math]\displaystyle{ T }[/math]将这个球面映射到[math]\displaystyle{ \mathbf{R}^m }[/math]中的一个椭球体。非零奇异值就是这个椭球体半轴(semi-axes)的长度。特别地,当[math]\displaystyle{ n=m }[/math]且所有奇异值都不同且非零时,线性映射[math]\displaystyle{ T }[/math]的SVD可以分解为三个连续步骤:
1. 考虑椭球体[math]\displaystyle{ T(S) }[/math]及其轴,然后找出[math]\displaystyle{ \mathbf{R}^n }[/math]中被[math]\displaystyle{ T }[/math]映射到这些轴上的方向。这些方向恰好相互正交。首先应用等距变换[math]\displaystyle{ \mathbf{V}^* }[/math],将这些方向映射到[math]\displaystyle{ \mathbf{R}^n }[/math]的坐标轴。
2. 应用沿坐标轴对角化的自同态(endomorphism 映射自身到自身的线性变换)[math]\displaystyle{ \mathbf{D} }[/math],在每个方向上进行拉伸或收缩,使用[math]\displaystyle{ T(S) }[/math]的半轴长度作为拉伸系数。组合[math]\displaystyle{ \mathbf{D} \circ \mathbf{V}^* }[/math]将单位球面映射到与[math]\displaystyle{ T(S) }[/math]等距的椭球体。
3. 最后,对这个椭球体应用等距变换[math]\displaystyle{ \mathbf{U} }[/math]以得到[math]\displaystyle{ T(S) }[/math]。
可以验证,组合[math]\displaystyle{ \mathbf{U} \circ \mathbf{D} \circ \mathbf{V}^* }[/math]与[math]\displaystyle{ T }[/math]一致。
案例
让我们来看一个[math]\displaystyle{ 4 \times 5 }[/math]矩阵的例子:
[math]\displaystyle{ \mathbf{M} = \begin{bmatrix} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{bmatrix} }[/math]
我们可以通过[math]\displaystyle{ \mathbf{U}\mathbf{\Sigma}\mathbf{V}^* }[/math]对该矩阵进行奇异值分解:
[math]\displaystyle{ \mathbf{U} = \begin{bmatrix} \color {Green}0&\color {Blue}-1&\color {Cyan}0&\color {Emerald}0 \\ \color {Green}-1&\color {Blue}0&\color {Cyan}0&\color {Emerald}0 \\ \color {Green}0&\color {Blue}0&\color {Cyan}0&\color {Emerald}-1 \\ \color {Green}0&\color {Blue}0&\color {Cyan}-1&\color {Emerald}0 \end{bmatrix} }[/math]
[math]\displaystyle{ \mathbf{\Sigma} = \begin{bmatrix} 3&0&0&0&\color {Gray}{\mathit {0}} \\ 0&{\sqrt {5}}&0&0&\color {Gray}{\mathit {0}} \\ 0&0&2&0&\color {Gray}{\mathit {0}} \\ 0&0&0&\color {Red}\mathbf {0} &\color {Gray}{\mathit {0}} \end{bmatrix} }[/math]
[math]\displaystyle{ \mathbf{V}^* = \begin{bmatrix} \color {Violet}0&\color {Violet}0&\color {Violet}-1&\color {Violet}0&\color {Violet}0 \\ \color {Plum}-{\sqrt {0.2}}&\color {Plum}0&\color {Plum}0&\color {Plum}0&\color {Plum}-{\sqrt {0.8}} \\ \color {Magenta}0&\color {Magenta}-1&\color {Magenta}0&\color {Magenta}0&\color {Magenta}0 \\ \color {Orchid}0&\color {Orchid}0&\color {Orchid}0&\color {Orchid}1&\color {Orchid}0 \\ \color {Purple}-{\sqrt {0.8}}&\color {Purple}0&\color {Purple}0&\color {Purple}0&\color {Purple}{\sqrt {0.2}} \end{bmatrix} }[/math]
注意,缩放矩阵[math]\displaystyle{ \mathbf{\Sigma} }[/math]在对角线以外的元素都为零(用灰色斜体表示),且有一个对角线元素为零(用红色粗体表示)。由于[math]\displaystyle{ \mathbf{U} }[/math]和[math]\displaystyle{ \mathbf{V}^* }[/math]都是酉矩阵,将它们分别与其共轭转置相乘会得到单位矩阵(identity matrices 对角线为1,其余为0的矩阵)。在这个例子中,[math]\displaystyle{ \mathbf{U} }[/math]和[math]\displaystyle{ \mathbf{V}^* }[/math]都是实值矩阵,因此它们都是正交矩阵(列向量互相正交且单位长度)。我们可以验证:
[math]\displaystyle{ \mathbf{U}\mathbf{U}^* = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} = \mathbf{I}_4 }[/math]
[math]\displaystyle{ \mathbf{V}\mathbf{V}^* = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix} = \mathbf{I}_5 }[/math]
值得注意的是,这个奇异值分解并非唯一。我们还可以选择另一个[math]\displaystyle{ \mathbf{V} }[/math],使得:
[math]\displaystyle{ \mathbf{V}^* = \begin{bmatrix} \color {Violet}0&\color {Violet}1&\color {Violet}0&\color {Violet}0&\color {Violet}0\\\color {Plum}0&\color {Plum}0&\color {Plum}1&\color {Plum}0&\color {Plum}0\\\color {Magenta}{\sqrt {0.2}}&\color {Magenta}0&\color {Magenta}0&\color {Magenta}0&\color {Magenta}{\sqrt {0.8}}\\\color {Orchid}{\sqrt {0.4}}&\color {Orchid}0&\color {Orchid}0&\color {Orchid}{\sqrt {0.5}}&\color {Orchid}-{\sqrt {0.1}}\\\color {Purple}-{\sqrt {0.4}}&\color {Purple}0&\color {Purple}0&\color {Purple}{\sqrt {0.5}}&\color {Purple}{\sqrt {0.1}} \end{bmatrix} }[/math]
这同样是一个有效的奇异值分解。
奇异值分解(SVD)和谱分解
奇异值、奇异向量及其与SVD的关系
非负实数 [math]\displaystyle{ \sigma }[/math] 称为 [math]\displaystyle{ \mathbf{M} }[/math] 的奇异值,当且仅当存在 [math]\displaystyle{ K^m }[/math] 中的单位长度向量 [math]\displaystyle{ \mathbf{u} }[/math] 和 [math]\displaystyle{ K^n }[/math] 中的单位长度向量 [math]\displaystyle{ \mathbf{v} }[/math],满足:
[math]\displaystyle{ \begin{aligned} \mathbf{Mv} &= \sigma \mathbf{u}, \\ \mathbf{M}^*\mathbf{u} &= \sigma \mathbf{v}. \end{aligned} }[/math]
我们称向量 [math]\displaystyle{ \mathbf{u} }[/math] 和 [math]\displaystyle{ \mathbf{v} }[/math] 分别为 [math]\displaystyle{ \sigma }[/math] 的左奇异向量和右奇异向量。
在奇异值分解 [math]\displaystyle{ \mathbf{M} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^* }[/math] 中,[math]\displaystyle{ \mathbf{\Sigma} }[/math] 的对角线元素即为 [math]\displaystyle{ \mathbf{M} }[/math] 的奇异值。[math]\displaystyle{ \mathbf{U} }[/math] 和 [math]\displaystyle{ \mathbf{V} }[/math] 的前 [math]\displaystyle{ p = \min(m,n) }[/math] 列分别对应各奇异值的左奇异向量和右奇异向量。因此,上述定理表明:
- 一个 [math]\displaystyle{ m \times n }[/math] 矩阵 [math]\displaystyle{ \mathbf{M} }[/math] 最多有 [math]\displaystyle{ p }[/math] 个不同的奇异值。
- 我们总能在 [math]\displaystyle{ \mathbf{K^m} }[/math] 空间中找到一组酉基(即一组基向量,它们构成的矩阵是酉矩阵) [math]\displaystyle{ \mathbf{U} }[/math],其中部分基向量,张成了矩阵 [math]\displaystyle{ \mathbf{M} }[/math]中每个奇异值对应的左奇异向量。
- 同样地,在 [math]\displaystyle{ \mathbf{K^n} }[/math] 空间中也存在一组酉基 [math]\displaystyle{ \mathbf{V} }[/math],其中部分基向量,张成了矩阵 [math]\displaystyle{ \mathbf{M} }[/math]中每个奇异值对应的右奇异向量。
当我们能找到两个线性独立的左(或右)奇异向量时,我们称该奇异值为简并(degenerate)的。如果 [math]\displaystyle{ \mathbf{u}_1 }[/math] 和 [math]\displaystyle{ \mathbf{u}_2 }[/math] 是对应奇异值 [math]\displaystyle{ \sigma }[/math] 的两个左奇异向量,那么这两个向量的任何归一化线性组合也是对应奇异值 [math]\displaystyle{ \sigma }[/math] 的左奇异向量。右奇异向量也有类似性质。独立的左奇异向量和右奇异向量数量相同,它们分别出现在 [math]\displaystyle{ \mathbf{U} }[/math] 和 [math]\displaystyle{ \mathbf{V} }[/math] 的对应列中,这些列对应着 [math]\displaystyle{ \mathbf{\Sigma} }[/math] 中值为 [math]\displaystyle{ \sigma }[/math] 的对角元素。
特别地,奇异值为0的左奇异向量和右奇异向量分别包括 [math]\displaystyle{ \mathbf{M} }[/math] 的余核(cokernel 未被矩阵覆盖的输出空间)和核(kernel 矩阵映射为零的输入空间)中的所有单位向量。根据秩-零化度定理(rank–nullity theorem),如果 [math]\displaystyle{ m \neq n }[/math],它们的维数不可能相同。即使所有奇异值都非零,当 [math]\displaystyle{ m \gt n }[/math] 时,余核是非平凡(nontrivial)的,此时 [math]\displaystyle{ \mathbf{U} }[/math] 用余核中的 [math]\displaystyle{ m-n }[/math] 个正交向量填充。相反,当 [math]\displaystyle{ m \lt n }[/math] 时,[math]\displaystyle{ \mathbf{V} }[/math] 由核中的 [math]\displaystyle{ n-m }[/math] 个正交向量填充。然而,如果存在0的奇异值,[math]\displaystyle{ \mathbf{U} }[/math] 或 [math]\displaystyle{ \mathbf{V} }[/math] 的额外列已经作为左奇异向量或右奇异向量出现。
非简并奇异值总有唯一的左奇异向量和右奇异向量,只能乘以单位相位因子(unit-phase factor) [math]\displaystyle{ e^{i\varphi} }[/math](实数情况下,只能乘以正负号)。因此,如果方阵 [math]\displaystyle{ \mathbf{M} }[/math] 的所有奇异值都是非简并且非零的,那么它的奇异值分解是唯一的,只能对 [math]\displaystyle{ \mathbf{U} }[/math] 的一列乘以单位相位因子,同时对 [math]\displaystyle{ \mathbf{V} }[/math] 的相应列乘以相同的单位相位因子。总的来说,SVD 在对 [math]\displaystyle{ \mathbf{U} }[/math] 和 [math]\displaystyle{ \mathbf{V} }[/math] 的列向量(这些列向量张成每个奇异值的子空间)统一应用任意酉变换,以及对 [math]\displaystyle{ \mathbf{U} }[/math] 和 [math]\displaystyle{ \mathbf{V} }[/math] 的向量(这些向量分别张成 [math]\displaystyle{ \mathbf{M} }[/math] 的核和余核)应用任意酉变换的情况下是唯一的。
与特征值分解的关系
奇异值分解具有广泛适用性,可用于任何 [math]\displaystyle{ m \times n }[/math] 矩阵,而特征值分解(eigenvalue decomposition)仅限于可对角化的方阵。尽管如此,这两种分解方法仍有密切联系。
设 [math]\displaystyle{ \mathbf{M} }[/math] 的SVD为 [math]\displaystyle{ \mathbf{M} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^* }[/math],则以下两个等式成立:
[math]\displaystyle{ \begin{aligned} \mathbf{M}^*\mathbf{M} &= \mathbf{V}\mathbf{\Sigma}^*\mathbf{U}^*\mathbf{U}\mathbf{\Sigma}\mathbf{V}^* = \mathbf{V}(\mathbf{\Sigma}^*\mathbf{\Sigma})\mathbf{V}^*, \\ \mathbf{M}\mathbf{M}^* &= \mathbf{U}\mathbf{\Sigma}\mathbf{V}^*\mathbf{V}\mathbf{\Sigma}^*\mathbf{U}^* = \mathbf{U}(\mathbf{\Sigma}\mathbf{\Sigma}^*)\mathbf{U}^*. \end{aligned} }[/math]
等式右侧描述了左侧的特征值分解。由此可得:
- [math]\displaystyle{ \mathbf{V} }[/math] 的列(即右奇异向量)是 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 的特征向量(eigenvectors 矩阵变换不改变方向的向量)。
- [math]\displaystyle{ \mathbf{U} }[/math] 的列(即左奇异向量)是 [math]\displaystyle{ \mathbf{M}\mathbf{M}^* }[/math] 的特征向量。
- [math]\displaystyle{ \mathbf{\Sigma} }[/math] 的非零元素(即非零奇异值)是 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 或 [math]\displaystyle{ \mathbf{M}\mathbf{M}^* }[/math] 非零特征值(矩阵变换后缩放的因子)的平方根。
当 [math]\displaystyle{ \mathbf{M} }[/math] 为正规矩阵(normal matrix 与其共轭转置可交换的矩阵)时,根据谱定理(spectral theorem),我们可以用特征向量的基对其进行酉对角化,得到分解 [math]\displaystyle{ \mathbf{M} = \mathbf{U}\mathbf{D}\mathbf{U}^* }[/math]。其中 [math]\displaystyle{ \mathbf{U} }[/math] 是酉矩阵,[math]\displaystyle{ \mathbf{D} }[/math] 是对角线上有复数元素 [math]\displaystyle{ \sigma_i }[/math] 的对角矩阵。若 [math]\displaystyle{ \mathbf{M} }[/math] 为半正定(positive semi-definite 所有特征值非负的矩阵)矩阵,则 [math]\displaystyle{ \sigma_i }[/math] 为非负实数,此时分解 [math]\displaystyle{ \mathbf{M} = \mathbf{U}\mathbf{D}\mathbf{U}^* }[/math] 也是一个奇异值分解。否则,我们可以将每个 [math]\displaystyle{ \sigma_i }[/math] 的相位 [math]\displaystyle{ e^{i\varphi} }[/math] 移到相应的 [math]\displaystyle{ \mathbf{V}_i }[/math] 或 [math]\displaystyle{ \mathbf{U}_i }[/math] 中,从而重新表示为SVD形式。SVD与非正规矩阵的联系主要体现在极分解定理:[math]\displaystyle{ \mathbf{M} = \mathbf{S}\mathbf{R} }[/math],其中 [math]\displaystyle{ \mathbf{S} = \mathbf{U}\mathbf{\Sigma}\mathbf{U}^* }[/math] 是半正定且正规的,[math]\displaystyle{ \mathbf{R} = \mathbf{U}\mathbf{V}^* }[/math] 是酉的。
因此,除半正定矩阵外,[math]\displaystyle{ \mathbf{M} }[/math] 的特征值分解和SVD虽有关联,但并不相同:特征值分解形如 [math]\displaystyle{ \mathbf{M} = \mathbf{U}\mathbf{D}\mathbf{U}^{-1} }[/math],其中 [math]\displaystyle{ \mathbf{U} }[/math] 不一定是酉的,[math]\displaystyle{ \mathbf{D} }[/math] 不一定是半正定的;而SVD形如 [math]\displaystyle{ \mathbf{M} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^* }[/math],其中 [math]\displaystyle{ \mathbf{\Sigma} }[/math] 是对角的且半正定的,[math]\displaystyle{ \mathbf{U} }[/math] 和 [math]\displaystyle{ \mathbf{V} }[/math] 是酉矩阵,它们除了通过矩阵 [math]\displaystyle{ \mathbf{M} }[/math] 外不一定有关联。值得注意的是,只有非亏损(non-defective 矩阵行列式不为零)方阵才有特征值分解,而任何 [math]\displaystyle{ m \times n }[/math] 矩阵都存在SVD。
奇异值分解的应用
伪逆
我们可以利用奇异值分解计算矩阵的伪逆(矩阵的广义逆,用于求解方程)。设矩阵 [math]\displaystyle{ \mathbf{M} }[/math] 的奇异值分解为 [math]\displaystyle{ \mathbf{M} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^* }[/math],则其伪逆为:
[math]\displaystyle{ \mathbf{M}^+ = \mathbf{V}\mathbf{\Sigma}^+\mathbf{U}^* }[/math]
这里,[math]\displaystyle{ \mathbf{\Sigma}^+ }[/math] 是 [math]\displaystyle{ \mathbf{\Sigma} }[/math] 的伪逆,我们通过将每个非零对角元素取倒数并转置来得到它。伪逆在解决线性最小二乘问题(linear least squares problems)时常常派上用场。
求解齐次线性方程
我们可以将一组齐次线性方程(homogeneous linear equations)表示为 [math]\displaystyle{ \mathbf{A}\mathbf{x} = \mathbf{0} }[/math],其中 [math]\displaystyle{ \mathbf{A} }[/math] 是矩阵,[math]\displaystyle{ \mathbf{x} }[/math] 是向量。通常,我们已知 [math]\displaystyle{ \mathbf{A} }[/math],需要找出满足方程的非零 [math]\displaystyle{ \mathbf{x} }[/math]。这样的 [math]\displaystyle{ \mathbf{x} }[/math] 属于 [math]\displaystyle{ \mathbf{A} }[/math] 的零空间,也称为 [math]\displaystyle{ \mathbf{A} }[/math] 的(右)零向量。我们可以将向量 [math]\displaystyle{ \mathbf{x} }[/math] 描述为与 [math]\displaystyle{ \mathbf{A} }[/math] 的零奇异值对应的右奇异向量。这意味着,如果 [math]\displaystyle{ \mathbf{A} }[/math] 是方阵且没有零奇异值,则方程没有非零解。若有多个零奇异值,那么对应的右奇异向量的任意线性组合都是有效解。类似地,满足 [math]\displaystyle{ \mathbf{x}^*\mathbf{A} = \mathbf{0} }[/math] 的非零 [math]\displaystyle{ \mathbf{x} }[/math](其中 [math]\displaystyle{ \mathbf{x}^* }[/math] 是 [math]\displaystyle{ \mathbf{x} }[/math] 的共轭转置)被称为 [math]\displaystyle{ \mathbf{A} }[/math] 的左零向量。
总体最小二乘最小化
总体最小二乘问题(total least squares)旨在找到一个向量 [math]\displaystyle{ \mathbf{x} }[/math],使得在 [math]\displaystyle{ \|\mathbf{x}\| = 1 }[/math] 的约束下(用双竖线 "||" 包围向量表示对该向量求范数),[math]\displaystyle{ \mathbf{A}\mathbf{x} }[/math] 的2-范数(2-norm)最小。结果表明,解就是 [math]\displaystyle{ \mathbf{A} }[/math] 最小奇异值对应的右奇异向量。
值域、零空间和秩
SVD还能为矩阵 [math]\displaystyle{ \mathbf{M} }[/math] 的值域和零空间提供明确表示。[math]\displaystyle{ \mathbf{M} }[/math] 零奇异值对应的右奇异向量张成(span)其零空间,非零奇异值对应的左奇异向量张成其值域。例如,在前面的例子中,零空间由 [math]\displaystyle{ \mathbf{V}^* }[/math] 的最后 [math]\displaystyle{ (n-r) }[/math]列张成,值域由 [math]\displaystyle{ \mathbf{U} }[/math] 的前 [math]\displaystyle{ r }[/math] 列张成,其中 [math]\displaystyle{ r }[/math] 是矩阵 [math]\displaystyle{ \mathbf{M} }[/math] 的秩。
因此,[math]\displaystyle{ \mathbf{M} }[/math] 的秩等于非零奇异值的个数,也就是 [math]\displaystyle{ \mathbf{\Sigma} }[/math] 中非零对角元素的个数。在数值线性代数中,我们可以用奇异值确定矩阵的有效秩,因为舍入误差(rounding error)可能导致秩亏矩阵(rank deficiency matrix)出现小但非零的奇异值。我们通常认为超过显著间隙的奇异值在数值上等同于零。
低秩矩阵近似
一些实际应用需要用另一个特定秩 r 的矩阵 [math]\displaystyle{ \tilde{\mathbf{M}} }[/math](称为截断矩阵truncated)来近似矩阵 [math]\displaystyle{ \mathbf{M} }[/math]。如果我们要在 [math]\displaystyle{ \operatorname{rank}(\tilde{\mathbf{M}}) = r }[/math] 的约束下最小化 [math]\displaystyle{ \mathbf{M} }[/math] 和 [math]\displaystyle{ \tilde{\mathbf{M}} }[/math] 之间差的Frobenius范数,那么解就由 [math]\displaystyle{ \mathbf{M} }[/math] 的SVD给出:
[math]\displaystyle{ \tilde{\mathbf{M}} = \mathbf{U}\tilde{\mathbf{\Sigma}}\mathbf{V}^* }[/math]
这里,[math]\displaystyle{ \tilde{\mathbf{\Sigma}} }[/math] 与 [math]\displaystyle{ \mathbf{\Sigma} }[/math] 相同,但只保留 r 个最大的奇异值(其他奇异值置零)。这就是Eckart–Young定理,由这两位作者于1936年证明(尽管后来发现早期学者已经了解这一结果)[1]。
可分离模型
我们可以将SVD视为把矩阵分解成加权、有序的可分离矩阵之和。所谓可分离,指的是矩阵 [math]\displaystyle{ \mathbf{A} }[/math] 可以表示为两个向量的外积(outer product 两个向量的反对称积,生成矩阵)[math]\displaystyle{ \mathbf{A} = \mathbf{u} \otimes \mathbf{v} }[/math],用坐标表示即 [math]\displaystyle{ A_{ij} = u_i v_j }[/math]。具体来说,矩阵 [math]\displaystyle{ \mathbf{M} }[/math] 的分解如下:
[math]\displaystyle{ \mathbf{M} = \sum_i \mathbf{A}_i = \sum_i \sigma_i \mathbf{U}_i \otimes \mathbf{V}_i }[/math]
这里,[math]\displaystyle{ \mathbf{U}_i }[/math] 和 [math]\displaystyle{ \mathbf{V}_i }[/math] 分别是SVD矩阵的第i列,[math]\displaystyle{ \sigma_i }[/math] 是有序奇异值,每个 [math]\displaystyle{ \mathbf{A}_i }[/math] 都是可分离的。在图像处理中,我们常用SVD将滤波器分解为水平和垂直的可分离滤波器。值得注意的是,非零 [math]\displaystyle{ \sigma_i }[/math] 的数量恰好等于矩阵的秩。
可分离模型在生物系统中很常见,SVD分解在分析这些系统时非常有用。例如,我们可以用空间域的Gabor滤波器乘以时间域的调制函数来很好地描述一些视觉区V1简单细胞的感受野[2]。因此,如果我们通过反向相关(reverse correlation)等方法评估得到线性滤波器,就可以将两个空间维度重排为一个维度,得到一个二维滤波器(空间,时间),然后进行SVD分解。在SVD分解中,[math]\displaystyle{ \mathbf{U} }[/math] 的第一列就是Gabor,而 [math]\displaystyle{ \mathbf{V} }[/math] 的第一列代表时间调制(或反之)。
我们可以定义一个可分离性指数:
[math]\displaystyle{ \alpha = \frac{\sigma_1^2}{\sum_i \sigma_i^2} }[/math]
该指数表明在矩阵[math]\displaystyle{ \mathbf{M} }[/math]的幂次中,第一个可分离矩阵所占的比例。[3]。
最近正交矩阵
我们可以利用方阵 [math]\displaystyle{ \mathbf{A} }[/math] 的SVD来找出最接近 [math]\displaystyle{ \mathbf{A} }[/math] 的正交矩阵(列向量互相正交且单位长度) [math]\displaystyle{ \mathbf{O} }[/math]。这里,我们用 [math]\displaystyle{ \mathbf{O} - \mathbf{A} }[/math] 的Frobenius范数来衡量接近程度。解是 [math]\displaystyle{ \mathbf{U}\mathbf{V}^* }[/math] 的乘积[4]。这个结果在直觉上是合理的,因为正交矩阵会有分解 [math]\displaystyle{ \mathbf{U}\mathbf{I}\mathbf{V}^* }[/math],其中 [math]\displaystyle{ \mathbf{I} }[/math] 是单位矩阵。所以如果 [math]\displaystyle{ \mathbf{A} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^* }[/math],那么乘积 [math]\displaystyle{ \mathbf{A} = \mathbf{U}\mathbf{V}^* }[/math] 相当于用1替换所有奇异值。等价地,解就是极分解 [math]\displaystyle{ \mathbf{M} = \mathbf{R}\mathbf{P} = \mathbf{P}'\mathbf{R} }[/math] 中的酉矩阵 [math]\displaystyle{ \mathbf{R} = \mathbf{U}\mathbf{V}^* }[/math],无论拉伸和旋转的顺序如何。
在形状分析中,有一个类似的问题叫做正交普鲁克问题(orthogonal Procrustes problem),它涉及找到一个最接近将 [math]\displaystyle{ \mathbf{A} }[/math] 映射到 [math]\displaystyle{ \mathbf{B} }[/math] 的正交矩阵 [math]\displaystyle{ \mathbf{O} }[/math]。具体来说:
[math]\displaystyle{ \mathbf{O} = \underset{\Omega}{\operatorname{argmin}} \|\mathbf{A}\mathbf{\Omega} - \mathbf{B}\|_F \quad \text{subject to} \quad \mathbf{\Omega}^T\mathbf{\Omega} = \mathbf{I} }[/math]
其中 [math]\displaystyle{ \|\cdot\|_F }[/math] 表示Frobenius范数。
这个问题等同于为给定矩阵 [math]\displaystyle{ \mathbf{M} = \mathbf{A}^T\mathbf{B} }[/math] 找到最近的正交矩阵。
Kabsch算法
Kabsch算法(在其他领域称为Wahba问题)运用SVD来计算最优旋转(关于最小二乘最小化),以将一组点与相应的另一组点对齐。这种算法在多个领域都有应用,比如用于比较分子结构。
信号处理
研究者已成功将SVD和伪逆应用于信号处理 [5]、图像处理 [6]和大数据(如基因组信号处理)[7][8][9][10] 。
其他例子
奇异值分解(SVD)在线性反问题(inverse problems)研究中广泛应用,分析Tikhonov正则化等方法时颇有助益。统计学界普遍使用它,与主成分分析(principal component analysis)和对应分析(correspondence analysis)密切相关,信号处理和模式识别领域也常见其身影。此外,它还用于仅输出模态分析(modal analysis),可从奇异向量确定非缩放模态形状(mode shapes)。自然语言文本处理中的潜在语义索引(latent semantic indexing)也离不开它。
在涉及线性或线性化系统的一般数值计算中,常用一个普遍常数来刻画问题的规律性或奇异性,即系统的"条件数" [math]\displaystyle{ \kappa := \sigma_{\text{max}} / \sigma_{\text{min}} }[/math]。这个数值通常决定了给定计算方案在这些系统上的误差率或收敛速度[11][12]。
量子信息(quantum information)领域中,SVD以Schmidt分解的形式发挥着关键作用。通过它,我们可以自然地分解两个量子系统的状态,从而提供了它们纠缠的充要条件:只要 [math]\displaystyle{ \mathbf{\Sigma} }[/math] 矩阵的秩大于1。
数值天气预报(numerical weather prediction)中,SVD对大型矩阵也有重要应用。利用Lanczos方法,可以估算在给定初始前向时间段内,对中心数值天气预报线性增长最快的几个扰动。这些扰动实际上是该时间间隔内全球天气线性化传播子对应最大奇异值的奇异向量。在这种情况下,输出奇异向量代表整个天气系统。随后,这些扰动通过完整的非线性模型运行,生成集合预报(ensemble forecast),为当前中心预测周围的不确定性提供了处理方法。
降阶建模(reduced-order modeling)中也少不了SVD的身影。降阶建模旨在减少复杂系统中的自由度数量。研究人员将SVD与径向基函数(radial basis functions)结合,用于插值三维非稳态流问题的解[13]。 值得一提的是,科学家们已经利用SVD改进了地面引力波干涉仪aLIGO的引力波形建模(gravitational wave modeling)[14]。SVD有助于提高波形生成的准确性和速度,支持引力波搜索和更新两种不同的波形模型。
推荐系统(Recommender systems)中,SVD用于预测用户对项目的评分[15]。为了在商品机器集群上高效计算SVD,研究人员开发了分布式算法[16]。
低秩SVD在从时空数据中检测热点方面表现出色,已应用于疾病爆发检测[17]。研究人员还将SVD和高阶SVD结合起来,用于疾病监测中从复杂数据流(具有空间和时间维度的多变量数据)进行实时事件检测[18]。
在天体动力学(astrodynamics)领域,科学家们运用SVD及其变体来确定转移轨道设计[19]和轨道站保持的合适机动方向[20]。
存在性证明
矩阵 [math]\displaystyle{ \mathbf{M} }[/math] 的特征值 [math]\displaystyle{ \lambda }[/math] 满足代数关系 [math]\displaystyle{ \mathbf{M}\mathbf{u} = \lambda\mathbf{u} }[/math]。当 [math]\displaystyle{ \mathbf{M} }[/math] 是厄米矩阵(Hermitian matrix 自共轭矩阵等于其共轭转置)时,我们还可以用变分特征来描述它。假设 [math]\displaystyle{ \mathbf{M} }[/math] 是一个 [math]\displaystyle{ n\times n }[/math] 的实数对称矩阵(矩阵等于其转置),我们定义函数:
[math]\displaystyle{ f:\left\{ \begin{aligned} \mathbb{R}^n &\to \mathbb{R} \\ \mathbf{x} &\mapsto \mathbf{x}^{\operatorname{T}}\mathbf{M}\mathbf{x} \end{aligned} \right. }[/math]
极值定理告诉我们,当这个连续函数限制在单位球面 [math]\displaystyle{ \{\|\mathbf{x}\|=1\} }[/math] 上时,必在某点 [math]\displaystyle{ \mathbf{u} }[/math] 处达到最大值。根据拉格朗日乘数定理,[math]\displaystyle{ \mathbf{u} }[/math] 必然满足:
[math]\displaystyle{ \nabla \mathbf{u}^{\operatorname{T}}\mathbf{M}\mathbf{u} - \lambda \cdot \nabla \mathbf{u}^{\operatorname{T}}\mathbf{u} = 0 }[/math]
这里 [math]\displaystyle{ \lambda }[/math] 是某个实数,而 [math]\displaystyle{ \nabla }[/math] 表示相对于 [math]\displaystyle{ \mathbf{x} }[/math] 的del微分算子。利用 [math]\displaystyle{ \mathbf{M} }[/math] 的对称性,我们得到:
[math]\displaystyle{ \nabla \mathbf{x}^{\operatorname{T}}\mathbf{M}\mathbf{x} - \lambda \cdot \nabla \mathbf{x}^{\operatorname{T}}\mathbf{x} = 2(\mathbf{M} - \lambda \mathbf{I})\mathbf{x} }[/math]
因此,[math]\displaystyle{ \mathbf{M}\mathbf{u} = \lambda\mathbf{u} }[/math],这说明 [math]\displaystyle{ \mathbf{u} }[/math] 是 [math]\displaystyle{ \mathbf{M} }[/math] 的单位长度特征向量。对 [math]\displaystyle{ \mathbf{M} }[/math] 的每个单位长度特征向量 [math]\displaystyle{ \mathbf{v} }[/math],其特征值就是 [math]\displaystyle{ f(\mathbf{v}) }[/math],所以 [math]\displaystyle{ \lambda }[/math] 是 [math]\displaystyle{ \mathbf{M} }[/math] 的最大特征值。在 [math]\displaystyle{ \mathbf{u} }[/math] 的正交补上重复这个过程,我们就能得到次大特征值,依此类推。
复数厄米矩阵的情况,处理方法类似,只是此时 [math]\displaystyle{ f(\mathbf{x}) = \mathbf{x}^*\mathbf{M}\mathbf{x} }[/math] 变成了 2n 个实变量的实值函数。
奇异值的描述方法与特征值相似,我们可以用代数或变分原理来刻画它们。不过,与特征值不同,这里的 [math]\displaystyle{ \mathbf{M} }[/math] 不必是厄米矩阵或对称矩阵。
接下来,我们将从两个角度论证奇异值分解的存在性。
基于谱定理
设 [math]\displaystyle{ \mathbf{M} }[/math] 为 [math]\displaystyle{ m\times n }[/math] 复矩阵。由于 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 是半正定厄米矩阵,根据谱定理,我们可以找到一个 [math]\displaystyle{ n\times n }[/math] 酉矩阵 [math]\displaystyle{ \mathbf{V} }[/math],使得:
[math]\displaystyle{ \mathbf{V}^*\mathbf{M}^*\mathbf{M}\mathbf{V} = \bar{\mathbf{D}} = \begin{bmatrix}\mathbf{D} & 0 \\ 0 & 0\end{bmatrix}, }[/math]
这里 [math]\displaystyle{ \mathbf{D} }[/math] 是 [math]\displaystyle{ \ell\times\ell }[/math] 维的对角正定矩阵,[math]\displaystyle{ \ell }[/math] 表示 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 非零特征值的个数(可以证明 [math]\displaystyle{ \ell \leq \min(n,m) }[/math])。我们将 [math]\displaystyle{ \mathbf{V} }[/math] 定义为一个矩阵,其第 i 列是 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 对应特征值 [math]\displaystyle{ \bar{\mathbf{D}}_{ii} }[/math] 的特征向量。当 [math]\displaystyle{ j\gt \ell }[/math] 时,[math]\displaystyle{ \mathbf{V} }[/math] 的第 j 列是 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 零特征值(即 [math]\displaystyle{ \bar{\mathbf{D}}_{jj}=0 }[/math])对应的特征向量。我们可以将 [math]\displaystyle{ \mathbf{V} }[/math] 写成 [math]\displaystyle{ \mathbf{V} = [\mathbf{V}_1 \quad \mathbf{V}_2] }[/math],其中 [math]\displaystyle{ \mathbf{V}_1 }[/math] 和 [math]\displaystyle{ \mathbf{V}_2 }[/math] 的列分别包含 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 非零和零特征值对应的特征向量。用这种形式重写 [math]\displaystyle{ \mathbf{V} }[/math],方程就变成:
[math]\displaystyle{ \begin{bmatrix}\mathbf{V}_1^* \\ \mathbf{V}_2^*\end{bmatrix}\mathbf{M}^*\mathbf{M}\,[\mathbf{V}_1 \quad \mathbf{V}_2] = \begin{bmatrix} \mathbf{V}_1^*\mathbf{M}^*\mathbf{M}\mathbf{V}_1 & \mathbf{V}_1^*\mathbf{M}^*\mathbf{M}\mathbf{V}_2 \\ \mathbf{V}_2^*\mathbf{M}^*\mathbf{M}\mathbf{V}_1 & \mathbf{V}_2^*\mathbf{M}^*\mathbf{M}\mathbf{V}_2 \end{bmatrix} = \begin{bmatrix}\mathbf{D} & 0 \\ 0 & 0\end{bmatrix}. }[/math]
这意味着:
[math]\displaystyle{ \mathbf{V}_1^*\mathbf{M}^*\mathbf{M}\mathbf{V}_1 = \mathbf{D},\quad \mathbf{V}_2^*\mathbf{M}^*\mathbf{M}\mathbf{V}_2 = \mathbf{0}。 }[/math]
进一步,第二个方程表明 [math]\displaystyle{ \mathbf{M}\mathbf{V}_2 = \mathbf{0} }[/math]。此外,[math]\displaystyle{ \mathbf{V} }[/math] 的酉性质在 [math]\displaystyle{ \mathbf{V}_1 }[/math] 和 [math]\displaystyle{ \mathbf{V}_2 }[/math] 方面体现为:
[math]\displaystyle{ \begin{aligned} \mathbf{V}_1^*\mathbf{V}_1 &= \mathbf{I}_1, \\ \mathbf{V}_2^*\mathbf{V}_2 &= \mathbf{I}_2, \\ \mathbf{V}_1\mathbf{V}_1^* + \mathbf{V}_2\mathbf{V}_2^* &= \mathbf{I}_{12}, \end{aligned} }[/math]
这里单位矩阵的下标用来表示它们的不同维度。
现在我们定义:
[math]\displaystyle{ \mathbf{U}_1 = \mathbf{M}\mathbf{V}_1\mathbf{D}^{-\frac{1}{2}}。 }[/math]
那么,
[math]\displaystyle{ \mathbf{U}_1\mathbf{D}^{\frac{1}{2}}\mathbf{V}_1^* = \mathbf{M}\mathbf{V}_1\mathbf{D}^{-\frac{1}{2}}\mathbf{D}^{\frac{1}{2}}\mathbf{V}_1^* = \mathbf{M}(\mathbf{I} - \mathbf{V}_2\mathbf{V}_2^*) = \mathbf{M} - (\mathbf{M}\mathbf{V}_2)\mathbf{V}_2^* = \mathbf{M}, }[/math]
因为 [math]\displaystyle{ \mathbf{M}\mathbf{V}_2 = \mathbf{0} }[/math]。这也可以看作 [math]\displaystyle{ \mathbf{M}\mathbf{V}_1\mathbf{V}_1^* = \mathbf{M} }[/math] 的直接结果。换个角度看,如果 [math]\displaystyle{ \{\boldsymbol{v}_i\}_{i=1}^\ell }[/math] 是 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 对应非零特征值 [math]\displaystyle{ \{\lambda_i\}_{i=1}^\ell }[/math] 的特征向量集,那么 [math]\displaystyle{ \{\mathbf{M}\boldsymbol{v}_i\}_{i=1}^\ell }[/math] 就是一组正交向量,而 [math]\displaystyle{ \{\lambda_i^{-1/2}\mathbf{M}\boldsymbol{v}_i\}_{i=1}^\ell }[/math] 则是一组(通常不完全的)正交单位向量。这与上面使用的矩阵形式相符,其中 [math]\displaystyle{ \mathbf{V}_1 }[/math] 表示列为 [math]\displaystyle{ \{\boldsymbol{v}_i\}_{i=1}^\ell }[/math] 的矩阵,[math]\displaystyle{ \mathbf{V}_2 }[/math] 表示列为 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 零特征值对应特征向量的矩阵,[math]\displaystyle{ \mathbf{U}_1 }[/math] 表示列为向量 [math]\displaystyle{ \{\lambda_i^{-1/2}\mathbf{M}\boldsymbol{v}_i\}_{i=1}^\ell }[/math] 的矩阵。
我们发现这几乎就是所需的结果,只是 [math]\displaystyle{ \mathbf{U}_1 }[/math] 和 [math]\displaystyle{ \mathbf{V}_1 }[/math] 通常不是酉矩阵,因为它们可能不是方阵。然而,我们知道 [math]\displaystyle{ \mathbf{U}_1 }[/math] 的行数不小于列数,因为 [math]\displaystyle{ \mathbf{D} }[/math] 的维度不大于 m 和 n。此外,由于
[math]\displaystyle{ \mathbf{U}_1^*\mathbf{U}_1 = \mathbf{D}^{-\frac{1}{2}}\mathbf{V}_1^*\mathbf{M}^*\mathbf{M}\mathbf{V}_1\mathbf{D}^{-\frac{1}{2}} = \mathbf{D}^{-\frac{1}{2}}\mathbf{D}\mathbf{D}^{-\frac{1}{2}} = \mathbf{I}_1, }[/math]
[math]\displaystyle{ \mathbf{U}_1 }[/math] 中的列是正交单位的,可以扩展成一个正交基。这意味着我们可以选择 [math]\displaystyle{ \mathbf{U}_2 }[/math],使得 [math]\displaystyle{ \mathbf{U} = [\mathbf{U}_1 \quad \mathbf{U}_2] }[/math] 成为酉矩阵。
对于 [math]\displaystyle{ \mathbf{V}_1 }[/math],我们已经有 [math]\displaystyle{ \mathbf{V}_2 }[/math] 使其成为酉矩阵。现在,我们定义
[math]\displaystyle{ \mathbf{\Sigma} = \begin{bmatrix} \begin{bmatrix}\mathbf{D}^{\frac{1}{2}} & 0 \\ 0 & 0\end{bmatrix} \\ 0 \end{bmatrix}, }[/math]
其中我们添加或删除额外的零行,使零行的数量等于 [math]\displaystyle{ \mathbf{U}_2 }[/math] 的列数,从而使 [math]\displaystyle{ \mathbf{\Sigma} }[/math] 的整体维度等于 [math]\displaystyle{ m\times n }[/math]。那么
[math]\displaystyle{ \begin{bmatrix}\mathbf{U}_1 & \mathbf{U}_2\end{bmatrix} \begin{bmatrix} \begin{bmatrix}\mathbf{D}^{\frac{1}{2}} & 0 \\ 0 & 0\end{bmatrix} \\ 0 \end{bmatrix} \begin{bmatrix}\mathbf{V}_1 & \mathbf{V}_2\end{bmatrix}^* = \begin{bmatrix}\mathbf{U}_1 & \mathbf{U}_2\end{bmatrix} \begin{bmatrix}\mathbf{D}^{\frac{1}{2}}\mathbf{V}_1^* \\ 0\end{bmatrix} = \mathbf{U}_1\mathbf{D}^{\frac{1}{2}}\mathbf{V}_1^* = \mathbf{M}, }[/math]
这就是我们要证明的结果:
[math]\displaystyle{ \mathbf{M} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^*。 }[/math]
值得注意的是,这个论证也可以从对角化 [math]\displaystyle{ \mathbf{M}\mathbf{M}^* }[/math] 而不是 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 开始(这直接显示 [math]\displaystyle{ \mathbf{M}\mathbf{M}^* }[/math] 和 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 具有相同的非零特征值)。
基于变分表征(variational characterization)
奇异值可描述为 [math]\displaystyle{ \mathbf{u}^{\mathrm{T}}\mathbf{M}\mathbf{v} }[/math] 的最大值,这是 [math]\displaystyle{ \mathbf{U} }[/math] 和 [math]\displaystyle{ \mathbf{V} }[/math] 在特定子空间上的函数。当达到这些最大值时, [math]\displaystyle{ \mathbf{U} }[/math] 和 [math]\displaystyle{ \mathbf{V} }[/math] 的值就是奇异向量。
设 [math]\displaystyle{ \mathbf{M} }[/math] 为 [math]\displaystyle{ m\times n }[/math] 实矩阵。定义 [math]\displaystyle{ S^{k-1} }[/math] 为 [math]\displaystyle{ \mathbb{R}^{k} }[/math] 中的单位 [math]\displaystyle{ (k-1) }[/math]-球面,并令 [math]\displaystyle{ \sigma(\mathbf{u},\mathbf{v})=\mathbf{u}^{\operatorname{T}}\mathbf{M}\mathbf{v} }[/math],其中 [math]\displaystyle{ \mathbf{u} \in S^{m-1} }[/math], [math]\displaystyle{ \mathbf{v} \in S^{n-1} }[/math]。
考虑函数 [math]\displaystyle{ \sigma }[/math] 在 [math]\displaystyle{ S^{m-1}\times S^{n-1} }[/math] 上的限制。由于 [math]\displaystyle{ S^{m-1} }[/math] 和 [math]\displaystyle{ S^{n-1} }[/math] 都是紧集(compact sets),它们的乘积也是紧集。又因 [math]\displaystyle{ \sigma }[/math] 连续,它必在 [math]\displaystyle{ S^{m-1} }[/math] 中的某向量 [math]\displaystyle{ \mathbf{u} }[/math] 和 [math]\displaystyle{ S^{n-1} }[/math] 中的某向量 [math]\displaystyle{ \mathbf{v} }[/math] 处达到最大值。我们将这个最大值记为 [math]\displaystyle{ \sigma_1 }[/math],相应的向量记为 [math]\displaystyle{ \mathbf{u}_1 }[/math] 和 [math]\displaystyle{ \mathbf{v}_1 }[/math]。由于 [math]\displaystyle{ \sigma_1 }[/math] 是 [math]\displaystyle{ \sigma(\mathbf{u},\mathbf{v}) }[/math] 的最大值,它必为非负。若为负,改变 [math]\displaystyle{ \mathbf{u}_1 }[/math] 或 [math]\displaystyle{ \mathbf{v}_1 }[/math] 的符号就能使其变为正值,从而更大。
现在我们提出以下陈述: [math]\displaystyle{ \mathbf{u}_1 }[/math] 和 [math]\displaystyle{ \mathbf{v}_1 }[/math] 是 [math]\displaystyle{ \mathbf{M} }[/math] 的左右奇异向量,对应的奇异值为 [math]\displaystyle{ \sigma_1 }[/math]。
证明如下:类似于特征值的情况,根据假设,这两个向量满足拉格朗日乘数方程:
[math]\displaystyle{ \nabla \sigma = \nabla \mathbf{u}^{\operatorname{T}}\mathbf{M}\mathbf{v} - \lambda_1 \cdot \nabla \mathbf{u}^{\operatorname{T}}\mathbf{u} - \lambda_2 \cdot \nabla \mathbf{v}^{\operatorname{T}}\mathbf{v} }[/math]
经过一些代数运算,我们得到:
[math]\displaystyle{ \begin{aligned} \mathbf{M}\mathbf{v}_1 &= 2\lambda_1\mathbf{u}_1 + 0,\\ \mathbf{M}^{\operatorname{T}}\mathbf{u}_1 &= 0 + 2\lambda_2\mathbf{v}_1. \end{aligned} }[/math]
从左侧将第一个方程乘以 [math]\displaystyle{ \mathbf{u}_1^{\textrm{T}} }[/math],第二个方程乘以 [math]\displaystyle{ \mathbf{v}_1^{\textrm{T}} }[/math],并考虑到 [math]\displaystyle{ \|\mathbf{u}\| = \|\mathbf{v}\| = 1 }[/math],我们得到:
[math]\displaystyle{ \sigma_1 = 2\lambda_1 = 2\lambda_2. }[/math]
将此代入上面的一对方程中,得:
[math]\displaystyle{ \begin{aligned} \mathbf{M}\mathbf{v}_1 &= \sigma_1\mathbf{u}_1,\\ \mathbf{M}^{\operatorname{T}}\mathbf{u}_1 &= \sigma_1\mathbf{v}_1. \end{aligned} }[/math]
这就证明了该陈述。
要找到更多的奇异向量和奇异值,我们可以在正交于 [math]\displaystyle{ \mathbf{u}_1 }[/math] 和 [math]\displaystyle{ \mathbf{v}_1 }[/math] 的归一化 [math]\displaystyle{ \mathbf{u} }[/math] 和 [math]\displaystyle{ \mathbf{v} }[/math] 上最大化 [math]\displaystyle{ \sigma(\mathbf{u},\mathbf{v}) }[/math]。
从实数到复数的过渡与特征值的情况类似。
计算奇异值分解(SVD)
单边雅可比算法(One-sided Jacobi algorithm)
单边雅可比算法是一种迭代算法[21],它通过反复转换使矩阵列正交化。其基本迭代步骤由雅可比旋转(Jacobi rotation)给出:
[math]\displaystyle{ M \leftarrow MJ(p,q,\theta), }[/math]
这里,我们选择雅可比旋转矩阵[math]\displaystyle{ J(p,q,\theta) }[/math]的角度[math]\displaystyle{ \theta }[/math],使旋转后第[math]\displaystyle{ p }[/math]列和第[math]\displaystyle{ q }[/math]列正交。指标[math]\displaystyle{ (p,q) }[/math]按[math]\displaystyle{ (p=1\dots m,q=p+1\dots m) }[/math]循环扫描,其中[math]\displaystyle{ m }[/math]为列数。
算法收敛后,我们可以这样恢复奇异值分解[math]\displaystyle{ M=USV^{T} }[/math]:矩阵[math]\displaystyle{ V }[/math]是雅可比旋转矩阵的累积,将转换后矩阵[math]\displaystyle{ M }[/math]的列归一化得到矩阵[math]\displaystyle{ U }[/math],而奇异值则由转换后矩阵[math]\displaystyle{ M }[/math]列的范数给出。
双边雅可比算法(Two-sided Jacobi algorithm)
双边雅可比SVD算法是雅可比特征值算法(Jacobi eigenvalue algorithm)的推广,它通过迭代将方阵转换为对角矩阵。对于非方阵,我们先进行QR分解,然后对[math]\displaystyle{ R }[/math]矩阵应用此算法。其基本迭代步骤如下:先用Givens旋转使一对非对角元素对称,再用雅可比变换(Jacobi transformation)使它们归零,
[math]\displaystyle{ M \leftarrow J^{T}GMJ }[/math]
这里,[math]\displaystyle{ G }[/math]是Givens旋转矩阵,我们选择适当的角度使指定的非对角元素对在旋转后相等;[math]\displaystyle{ J }[/math]是雅可比变换矩阵,用于将这些非对角元素置零。迭代过程与雅可比特征值算法相同:对所有非对角元素循环扫描。
算法收敛后,结果对角矩阵包含奇异值。矩阵[math]\displaystyle{ U }[/math]和[math]\displaystyle{ V }[/math]的累积如下:[math]\displaystyle{ U \leftarrow UG^{T}J }[/math],[math]\displaystyle{ V \leftarrow VJ }[/math]。
数值方法
我们可以利用以下观察结果计算奇异值分解:
- [math]\displaystyle{ \mathbf{M} }[/math]的左奇异向量是[math]\displaystyle{ \mathbf{M}\mathbf{M}^{*} }[/math]的一组正交归一化特征向量。
- [math]\displaystyle{ \mathbf{M} }[/math]的右奇异向量是[math]\displaystyle{ \mathbf{M}^{*}\mathbf{M} }[/math]的一组正交归一化特征向量。
- [math]\displaystyle{ \mathbf{M} }[/math]的非零奇异值(在[math]\displaystyle{ \mathbf{\Sigma} }[/math]的对角线上)等于[math]\displaystyle{ \mathbf{M}^{*}\mathbf{M} }[/math]和[math]\displaystyle{ \mathbf{M}\mathbf{M}^{*} }[/math]的非零特征值的平方根。
通常,我们通过两步计算矩阵[math]\displaystyle{ \mathbf{M} }[/math]的SVD。第一步将矩阵简化为双对角矩阵(bidiagonal matrix),假设[math]\displaystyle{ m \geq n }[/math],需要[math]\displaystyle{ O(mn^{2}) }[/math]次浮点运算(flop)。第二步计算双对角矩阵的SVD,只能通过迭代方法完成。实际上,计算到机器精度就足够了。如果将这个精度视为常数,第二步需要[math]\displaystyle{ O(n) }[/math]次迭代,每次迭代花费[math]\displaystyle{ O(n) }[/math]次flop。因此,第一步耗时更长,总体成本为[math]\displaystyle{ O(mn^{2}) }[/math]次flop[22]。
如果只需计算奇异值,第一步可用Householder反射以[math]\displaystyle{ 4mn^{2}-4n^{3}/3 }[/math]次flop完成。当[math]\displaystyle{ m }[/math]远大于[math]\displaystyle{ n }[/math]时,先用QR分解将矩阵[math]\displaystyle{ \mathbf{M} }[/math]简化为三角矩阵,再用Householder反射进一步简化为双对角形式更有优势;总成本为[math]\displaystyle{ 2mn^{2}+2n^{3} }[/math]次flop[22]。
第二步可用QR算法的变体完成,该变体由Golub & Kahan[23]首次描述。LAPACK子程序DBDSQR[24]实现了这种迭代方法,并针对奇异值非常小的情况进行了改进[25]。结合使用Householder反射的第一步和适当情况下的QR分解,构成了计算奇异值分解的DGESVD[24]例程。
GNU科学库(GSL)也实现了相同算法,并提供了一种替代方法,在第2步中使用单边雅可比正交化[26]。这种方法通过求解一系列[math]\displaystyle{ 2\times 2 }[/math]的SVD问题来计算双对角矩阵的SVD,类似于雅可比特征值算法求解一系列[math]\displaystyle{ 2\times 2 }[/math]的特征值问题[27]。第2步的另一种方法借鉴了分治特征值算法(divide-and-conquer eigenvalue algorithms)的思想[22]。
还有一种不显式使用特征值分解的替代方法[28]。通常,我们将矩阵[math]\displaystyle{ \mathbf{M} }[/math]的奇异值问题转换为等价的对称特征值问题,如[math]\displaystyle{ \mathbf{M}\mathbf{M}^{*} }[/math],[math]\displaystyle{ \mathbf{M}^{*}\mathbf{M} }[/math],或 [math]\displaystyle{ \begin{bmatrix}\mathbf{0} &\mathbf{M} \\\mathbf{M}^{*}&\mathbf{0} \end{bmatrix}. }[/math]
使用特征值分解的方法基于QR算法,该算法已发展得稳定且快速。注意,奇异值是实数,右奇异向量和左奇异向量不需要形成相似变换。我们可以在QR分解和LQ分解之间迭代交替以找到实对角厄米矩阵。QR分解给出[math]\displaystyle{ \mathbf{M} \Rightarrow \mathbf{Q}\mathbf{R} }[/math],[math]\displaystyle{ \mathbf{R} }[/math]的LQ分解给出[math]\displaystyle{ \mathbf{R} \Rightarrow \mathbf{L}\mathbf{P}^{*} }[/math]。因此,每次迭代中,我们有[math]\displaystyle{ \mathbf{M} \Rightarrow \mathbf{Q}\mathbf{L}\mathbf{P}^{*} }[/math],更新[math]\displaystyle{ \mathbf{M} \Leftarrow \mathbf{L} }[/math]并重复正交化。最终,QR分解和LQ分解之间的这种迭代产生左右酉奇异矩阵。这种方法不能像QR算法那样通过谱移位或缩减来加速,因为没有使用相似变换,移位方法不易定义。然而,这种迭代方法实现简单,当速度不重要时是个不错的选择。它还提供了纯正交/酉变换如何获得SVD的洞察。
2 × 2 SVD的解析结果
解析[math]\displaystyle{ 2\times 2 }[/math],我们可以找到矩阵的奇异值。设矩阵为[math]\displaystyle{ \mathbf{M} =z_{0}\mathbf{I} +z_{1}\sigma_{1}+z_{2}\sigma_{2}+z_{3}\sigma_{3} }[/math]
其中[math]\displaystyle{ z_{i}\in \mathbb{C} }[/math]是参数化矩阵的复数,[math]\displaystyle{ \mathbf{I} }[/math]是单位矩阵,[math]\displaystyle{ \sigma_{i} }[/math]表示泡利矩阵(Pauli matrices)。那么它的两个奇异值由以下给出:
[math]\displaystyle{ \begin{aligned} \sigma_{\pm} &= \sqrt{|z_{0}|^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2}\pm \sqrt{(|z_{0}|^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2})^{2}-|z_{0}^{2}-z_{1}^{2}-z_{2}^{2}-z_{3}^{2}|^{2}}} \\ &= \sqrt{|z_{0}|^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2}\pm 2\sqrt{(\operatorname{Re} z_{0}z_{1}^{*})^{2}+(\operatorname{Re} z_{0}z_{2}^{*})^{2}+(\operatorname{Re} z_{0}z_{3}^{*})^{2}+(\operatorname{Im} z_{1}z_{2}^{*})^{2}+(\operatorname{Im} z_{2}z_{3}^{*})^{2}+(\operatorname{Im} z_{3}z_{1}^{*})^{2}}} \end{aligned} }[/math]
简化奇异值分解
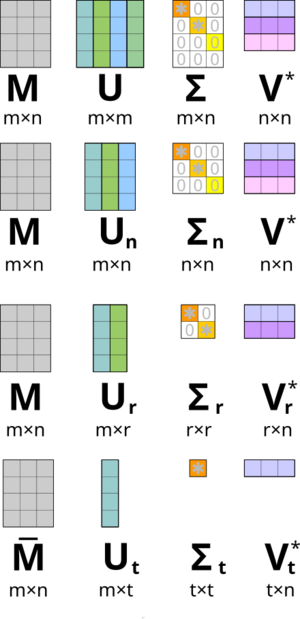
在实际应用中,我们很少需要完全SVD,包括矩阵零空间的完整酉分解。相反,上图中的计算简化版的SVD通常就够用了(而且更快,更省存储空间)。对于一个秩为r的[math]\displaystyle{ m \times n }[/math]矩阵[math]\displaystyle{ \mathbf{M} }[/math],我们可以区分以下几种情况:
薄SVD (Thin SVD)
矩阵[math]\displaystyle{ \mathbf{M} }[/math]的薄SVD(又叫经济型SVD)可表示为[29]:
这里[math]\displaystyle{ k = \min(m,n) }[/math],矩阵[math]\displaystyle{ \mathbf{U}_k }[/math]和[math]\displaystyle{ \mathbf{V}_k }[/math]只包含[math]\displaystyle{ \mathbf{U} }[/math]和[math]\displaystyle{ \mathbf{V} }[/math]的前k列,[math]\displaystyle{ \mathbf{\Sigma}_k }[/math]只包含[math]\displaystyle{ \mathbf{\Sigma} }[/math]中的前k个奇异值。因此,矩阵[math]\displaystyle{ \mathbf{U}_k }[/math]为[math]\displaystyle{ m \times k }[/math],[math]\displaystyle{ \mathbf{\Sigma}_k }[/math]为[math]\displaystyle{ k \times k }[/math]对角矩阵,[math]\displaystyle{ \mathbf{V}_k^* }[/math]为[math]\displaystyle{ k \times n }[/math]。
当[math]\displaystyle{ k \ll \max(m,n) }[/math]时,薄SVD能大大节省空间和计算时间。它的计算通常先对[math]\displaystyle{ \mathbf{M} }[/math]做QR分解,这样能显著加快运算速度。
紧凑SVD (Compact SVD)
矩阵[math]\displaystyle{ \mathbf{M} }[/math]的紧凑SVD可表示为:
[math]\displaystyle{ \mathbf{M} = \mathbf{U}_r \mathbf{\Sigma}_r \mathbf{V}_r^*. }[/math]
我们只计算[math]\displaystyle{ \mathbf{U} }[/math]的r个列向量和[math]\displaystyle{ \mathbf{V}^* }[/math]的r个行向量,它们对应非零奇异值[math]\displaystyle{ \mathbf{\Sigma}_r }[/math]。[math]\displaystyle{ \mathbf{U} }[/math]和[math]\displaystyle{ \mathbf{V}^* }[/math]的其余向量则不计算。当[math]\displaystyle{ r \ll \min(m,n) }[/math]时,这比薄SVD更快更省。因此,矩阵[math]\displaystyle{ \mathbf{U}_r }[/math]为[math]\displaystyle{ m \times r }[/math],[math]\displaystyle{ \mathbf{\Sigma}_r }[/math]为[math]\displaystyle{ r \times r }[/math]对角矩阵,[math]\displaystyle{ \mathbf{V}_r^* }[/math]为[math]\displaystyle{ r \times n }[/math]。
截断SVD (Truncated SVD)
在很多应用中,非零奇异值的数量r很大,使得即使紧凑SVD也难以计算。这时我们可能需要截断最小的奇异值,只计算[math]\displaystyle{ t \ll r }[/math]个非零奇异值。截断SVD不再是原始矩阵[math]\displaystyle{ \mathbf{M} }[/math]的精确分解,而是提供了一个固定秩t的最优低秩矩阵近似(low-rank matrix approximation)[math]\displaystyle{ \tilde{\mathbf{M}} }[/math]:
[math]\displaystyle{ \tilde{\mathbf{M}} = \mathbf{U}_t \mathbf{\Sigma}_t \mathbf{V}_t^*, }[/math]
这里矩阵[math]\displaystyle{ \mathbf{U}_t }[/math]为[math]\displaystyle{ m \times t }[/math],[math]\displaystyle{ \mathbf{\Sigma}_t }[/math]为[math]\displaystyle{ t \times t }[/math]对角矩阵,[math]\displaystyle{ \mathbf{V}_t^* }[/math]为[math]\displaystyle{ t \times n }[/math]。我们只计算[math]\displaystyle{ \mathbf{U} }[/math]的t个列向量和[math]\displaystyle{ \mathbf{V}^* }[/math]的t个行向量,它们对应[math]\displaystyle{ \mathbf{\Sigma}_t }[/math]中最大的t个奇异值。当[math]\displaystyle{ t \ll r }[/math]时,这比紧凑SVD更快更省,但需要一套完全不同的数值求解器工具。
在需要近似矩阵[math]\displaystyle{ \mathbf{M} }[/math]的Moore–Penrose逆的应用中,[math]\displaystyle{ \mathbf{M} }[/math]的最小奇异值是有意义的,但与最大奇异值相比,它们更难计算。
范数
Ky Fan范数
我们把[math]\displaystyle{ \mathbf{M} }[/math]的k个最大奇异值之和称为[math]\displaystyle{ \mathbf{M} }[/math]的Ky Fan k-范数,这是一种矩阵范数(matrix norm)[31]。
Ky Fan范数中的第一个,即Ky Fan 1-范数,等同于[math]\displaystyle{ \mathbf{M} }[/math]作为线性算子相对于[math]\displaystyle{ K^m }[/math]和[math]\displaystyle{ K^n }[/math]的欧几里得范数的算子范数(operator norm)。换言之,Ky Fan 1-范数就是标准[math]\displaystyle{ \ell^2 }[/math]欧几里得内积诱导的算子范数。我们很容易就能验证Ky Fan 1-范数和奇异值之间的关系。一般来说,对于(可能是无限维)希尔伯特空间上的有界算子[math]\displaystyle{ \mathbf{M} }[/math],我们有:
[math]\displaystyle{ \|\mathbf{M}\| = \|\mathbf{M}^*\mathbf{M}\|^{\frac{1}{2}} }[/math]
在矩阵情况下,[math]\displaystyle{ (\mathbf{M}^*\mathbf{M})^{1/2} }[/math]是个正规矩阵,所以[math]\displaystyle{ \|\mathbf{M}^*\mathbf{M}\|^{1/2} }[/math]就是[math]\displaystyle{ (\mathbf{M}^*\mathbf{M})^{1/2} }[/math]的最大特征值,也就是[math]\displaystyle{ \mathbf{M} }[/math]的最大奇异值。
Ky Fan范数中的最后一个,即所有奇异值的和,我们称之为迹范数(trace norm)(也叫核范数),定义为[math]\displaystyle{ \|\mathbf{M}\| = \operatorname{Tr}(\mathbf{M}^*\mathbf{M})^{1/2} }[/math]([math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math]的特征值是奇异值的平方)。
希尔伯特-施密特范数
奇异值还与算子空间上的另一个范数有关。我们来看看[math]\displaystyle{ n \times n }[/math]矩阵上的希尔伯特-施密特内积(Hilbert–Schmidt inner product),它的定义是:
[math]\displaystyle{ \langle \mathbf{M}, \mathbf{N} \rangle = \operatorname{tr}(\mathbf{N}^*\mathbf{M}). }[/math]
由此,诱导范数就是:
[math]\displaystyle{ \|\mathbf{M}\| = \sqrt{\langle \mathbf{M}, \mathbf{M} \rangle} = \sqrt{\operatorname{tr}(\mathbf{M}^*\mathbf{M})}. }[/math]
因为迹在酉等价下不变,所以我们可以得出:
[math]\displaystyle{ \|\mathbf{M}\| = \sqrt{\sum_i \sigma_i^2} }[/math]
这里[math]\displaystyle{ \sigma_i }[/math]是[math]\displaystyle{ \mathbf{M} }[/math]的奇异值。我们把这个称为[math]\displaystyle{ \mathbf{M} }[/math]的Frobenius范数、Schatten 2-范数或希尔伯特-施密特范数。直接计算可以发现,[math]\displaystyle{ \mathbf{M} = (m_{ij}) }[/math]的Frobenius范数与下式一致:
[math]\displaystyle{ \sqrt{\sum_{ij} |m_{ij}|^2}. }[/math]
值得一提的是,Frobenius范数和迹范数(核范数)都是Schatten范数的特殊情况。
变体和推广
尺度不变奇异值分解
矩阵 [math]\displaystyle{ \mathbf{A} }[/math] 的奇异值是唯一的,且对 [math]\displaystyle{ \mathbf{A} }[/math] 的左右酉变换保持不变。换句话说,对酉矩阵 [math]\displaystyle{ \mathbf{U} }[/math] 和 [math]\displaystyle{ \mathbf{V} }[/math],[math]\displaystyle{ \mathbf{U}\mathbf{A}\mathbf{V} }[/math] 的奇异值与 [math]\displaystyle{ \mathbf{A} }[/math] 的相同。这一重要性质适用于需要保持欧几里得距离和旋转不变性的应用。
尺度不变奇异值分解(SI-SVD)与常规奇异值分解相似,但其奇异值对 [math]\displaystyle{ \mathbf{A} }[/math] 的对角变换保持不变。也就是说,对可逆对角矩阵 [math]\displaystyle{ \mathbf{D} }[/math] 和 [math]\displaystyle{ \mathbf{E} }[/math],[math]\displaystyle{ \mathbf{D}\mathbf{A}\mathbf{E} }[/math] 的奇异值与 [math]\displaystyle{ \mathbf{A} }[/math] 的相同。这一性质在需要对变量单位选择(如公制与英制)保持不变的应用中尤为重要。
希尔伯特空间上的有界算子
我们可以将分解 [math]\displaystyle{ \mathbf{M} = \mathbf{U}\mathbf{\Sigma}\mathbf{V}^* }[/math] 推广到可分希尔伯特空间 [math]\displaystyle{ H }[/math] 上的有界算子(bounded operator)[math]\displaystyle{ \mathbf{M} }[/math]。具体来说,对任何有界算子 [math]\displaystyle{ \mathbf{M} }[/math],都存在部分等距(partial isometry)算子 [math]\displaystyle{ \mathbf{U} }[/math],酉算子 [math]\displaystyle{ \mathbf{V} }[/math],测度空间 [math]\displaystyle{ (X,\mu) }[/math],以及非负可测函数 [math]\displaystyle{ f }[/math],使得:
[math]\displaystyle{ \mathbf{M} = \mathbf{U}T_f\mathbf{V}^* }[/math]
这里 [math]\displaystyle{ T_f }[/math] 是 [math]\displaystyle{ L^2(X,\mu) }[/math] 上的 [math]\displaystyle{ f }[/math] 乘法算子。
我们可以通过模仿上述矩阵情况的线性代数论证来证明这一点。[math]\displaystyle{ \mathbf{V}T_f\mathbf{V}^* }[/math] 是 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 的唯一正平方根,这由自伴算子(self-adjoint operators)的Borel函数演算 (Borel functional calculus) 给出。[math]\displaystyle{ \mathbf{U} }[/math] 不必是酉的原因是,与有限维情况不同,给定具有非平凡核的等距算子 [math]\displaystyle{ U_1 }[/math],可能找不到合适的 [math]\displaystyle{ U_2 }[/math] 使得:
[math]\displaystyle{ \begin{bmatrix}U_1\\U_2\end{bmatrix} }[/math]
成为一个酉算子。
与矩阵类似,奇异值分解等价于算子的极分解:我们可以简单地写作:
[math]\displaystyle{ \mathbf{M} = \mathbf{U}\mathbf{V}^* \cdot \mathbf{V}T_f\mathbf{V}^* }[/math]
并注意到 [math]\displaystyle{ \mathbf{U}\mathbf{V}^* }[/math] 仍是部分等距算子,而 [math]\displaystyle{ \mathbf{V}T_f\mathbf{V}^* }[/math] 是正的。
奇异值和紧算子
我们可以将奇异值和左/右奇异向量的概念推广到希尔伯特空间上的紧算子(compact operator on Hilbert space),因为它们具有离散谱。如果 [math]\displaystyle{ T }[/math] 是紧的,其谱中的每个非零 [math]\displaystyle{ \lambda }[/math] 都是特征值。此外,紧自伴算子可由其特征向量对角化。如果 [math]\displaystyle{ \mathbf{M} }[/math] 是紧的,那么 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 也是紧的。应用对角化结果,其正平方根 [math]\displaystyle{ T_f }[/math] 的酉像有一组对应于严格正特征值 [math]\displaystyle{ \{\sigma_i\} }[/math] 的正交归一化特征向量 [math]\displaystyle{ \{e_i\} }[/math]。对 [math]\displaystyle{ H }[/math] 中的任意 [math]\displaystyle{ \psi }[/math],有:
[math]\displaystyle{ \mathbf{M}\psi = \mathbf{U}T_f\mathbf{V}^*\psi = \sum_i \langle \mathbf{U}T_f\mathbf{V}^*\psi, \mathbf{U}e_i \rangle \mathbf{U}e_i = \sum_i \sigma_i \langle \psi, \mathbf{V}e_i \rangle \mathbf{U}e_i, }[/math]
这里级数在 [math]\displaystyle{ H }[/math] 的范数拓扑中收敛。注意,这与有限维情况的表达式相似。我们称 [math]\displaystyle{ \sigma_i }[/math] 为 [math]\displaystyle{ \mathbf{M} }[/math] 的奇异值,[math]\displaystyle{ \{\mathbf{U}e_i\} }[/math] 和 [math]\displaystyle{ \{\mathbf{U}e_i\} }[/math] 分别为 [math]\displaystyle{ \mathbf{M} }[/math] 的左奇异和右奇异向量。
希尔伯特空间上的紧算子是有限秩算子(finite rank operator)在一致算子拓扑中的闭包。上述级数表达式给出了这种表示的一个明确例子。这直接导出以下结论:
定理:[math]\displaystyle{ \mathbf{M} }[/math] 是紧的当且仅当 [math]\displaystyle{ \mathbf{M}^*\mathbf{M} }[/math] 是紧的。
历史
奇异值分解最初源于微分几何学家的研究。他们希望确定能否通过对两个作用空间进行独立正交变换,使一个实双线性形式等同于另一个。1873年和1874年,Eugenio Beltrami 和 Camille Jordan 分别独立发现,双线性形式(用矩阵表示)的奇异值构成了正交替代下的完整不变量集(complete set of invariants)。1889年,James Joseph Sylvester 也独立得出了实方阵的奇异值分解,他将奇异值称为矩阵 [math]\displaystyle{ \mathbf{A} }[/math] 的规范乘子。1915年,Autonne 成为第四位独立发现者,他通过极分解推导出了奇异值分解。直到1936年,Carl Eckart 和 Gale J. Young 才首次证明了矩形和复矩阵的奇异值分解[32],他们将其视为厄米矩阵主轴变换的推广。
1907年,Erhard Schmidt 为积分算子(integral operators)(在某些弱技术假设下为紧算子)定义了类似奇异值的概念,他似乎不知道有关有限矩阵奇异值的平行研究。1910年,Émile Picard 进一步发展了这一理论,并首次将 [math]\displaystyle{ \sigma_k }[/math] 称为奇异值。
计算奇异值分解的实用方法可追溯到1954-1955年 Kogbetliantz 和1958年 Hestenes 的工作[33]。这些方法与使用平面旋转或 Givens 旋转的 Jacobi 特征值算法极为相似。然而,1965年 Gene Golub 和 William Kahan 发表的方法[23]取代了之前的方法,他们采用了 Householder 变换或反射。1970年,Golub 和 Christian Reinsch[34] 发表了 Golub/Kahan 算法的一个变体,这个变体至今仍广泛应用。
参考文献
- ↑ Stewart, G. W. (1993). "On the Early History of the Singular Value Decomposition". SIAM Review. 35 (4): 551–566. CiteSeerX 10.1.1.23.1831. doi:10.1137/1035134. hdl:1903/566. JSTOR 2132388.
- ↑ DeAngelis, G. C.; Ohzawa, I.; Freeman, R. D. (October 1995), ""Receptive-field dynamics in the central visual pathways"", Trends Neurosci, 18 (10): 451–8., doi:10.1016/0166-2236(95)94496-R, PMID 8545912, S2CID 12827601
- ↑ Depireux, D. A.; Simon, J. Z.; Klein, D. J.; Shamma, S. A. (March 2001), ""Spectro-temporal response field characterization with dynamic ripples in ferret primary auditory cortex"", J. Neurophysiol, 85 (3): 1220–34, doi:10.1152/jn.2001.85.3.1220, PMID 11247991
- ↑ The Singular Value Decomposition in Symmetric (Lowdin) Orthogonalization and Data Compression (PDF)
- ↑ Sahidullah, Md.; Kinnunen; Tomi (March 2016), ""Local spectral variability features for speaker verification"", Digital Signal Processing, 50: 1–11, doi:10.1016/j.dsp.2015.10.011
- ↑ Mademlis, Ioannis; Tefas, Anastasios; Pitas, Ioannis (2018), "Regularized SVD-Based Video Frame Saliency for Unsupervised Activity Video Summarization", IEEE, pp. 2691–2695, doi:10.1109/ICASSP.2018.8462274, ISBN 978-1-5386-4658-8, S2CID 52286352, retrieved 2023-01-19
- ↑ Alter, O.; Brown, P. O.; Botstein, D. (September 2000). "Singular Value Decomposition for Genome-Wide Expression Data Processing and Modeling". PNAS. 97 (18): 10101–10106. Bibcode:2000PNAS...9710101A. doi:10.1073/pnas.97.18.10101. PMC 27718. PMID 10963673.
- ↑ Alter, O.; Golub, G. H. (November 2004). "Integrative Analysis of Genome-Scale Data by Using Pseudoinverse Projection Predicts Novel Correlation Between DNA Replication and RNA Transcription". PNAS. 101 (47): 16577–16582. Bibcode:2004PNAS..10116577A. doi:10.1073/pnas.0406767101. PMC 534520. PMID 15545604.
- ↑ Alter, O.; Golub, G. H. (August 2006). "Singular Value Decomposition of Genome-Scale mRNA Lengths Distribution Reveals Asymmetry in RNA Gel Electrophoresis Band Broadening". PNAS. 103 (32): 11828–11833. Bibcode:2006PNAS..10311828A. doi:10.1073/pnas.0604756103. PMC 1524674. PMID 16877539.
- ↑ Bertagnolli, N. M.; Drake, J. A.; Tennessen, J. M.; Alter, O. (November 2013). "SVD Identifies Transcript Length Distribution Functions from DNA Microarray Data and Reveals Evolutionary Forces Globally Affecting GBM Metabolism". PLOS ONE. 8 (11): e78913. Bibcode:2013PLoSO...878913B. doi:10.1371/journal.pone.0078913. PMC 3839928. PMID 24282503.Highlight}
- ↑ Edelman, Alan (1992), ""On the distribution of a scaled condition number"" (PDF), Math. Comp., 58 (197): 185–190, Bibcode:1992MaCom..58..185E, doi:10.1090/S0025-5718-1992-1106966-2
- ↑ Shen, Jianhong (Jackie) (2001), ""On the singular values of Gaussian random matrices"", Linear Alg. Appl., 326 (1–3): 1–14, doi:10.1016/S0024-3795(00)00322-0
- ↑ Walton, S.; Hassan, O.; Morgan, K. (2013), ""Reduced order modelling for unsteady fluid flow using proper orthogonal decomposition and radial basis functions"", Applied Mathematical Modelling, 37 (20–21): 8930–8945, doi:10.1016/j.apm.2013.04.025
- ↑ Setyawati, Y.; Ohme, F.; Khan, S. (2019), ""Enhancing gravitational waveform model through dynamic calibration"", Physical Review D, 99 (2): 024010, arXiv:1810.07060, Bibcode:2019PhRvD..99b4010S, doi:10.1103/PhysRevD.99.024010, S2CID 118935941
- ↑ Sarwar, Badrul; Karypis, George; Konstan, Joseph A.; Riedl, John T. (2000), "Application of Dimensionality Reduction in Recommender System – A Case Study" (PDF), University of Minnesota
- ↑ Bosagh Zadeh, Reza; Carlsson, Gunnar (2013), "Dimension Independent Matrix Square Using MapReduce" (PDF), arXiv:1304.1467, Bibcode:2013arXiv1304.1467B
- ↑ Fanaee Tork, Hadi; Gama, João (September 2014), ""Eigenspace method for spatiotemporal hotspot detection"", Expert Systems, 32 (3): 454–464, arXiv:1406.3506, Bibcode:2014arXiv1406.3506F, doi:10.1111/exsy.12088, S2CID 15476557
- ↑ Fanaee Tork, Hadi; Gama, João (May 2015), ""EigenEvent: An Algorithm for Event Detection from Complex Data Streams in Syndromic Surveillance"", Intelligent Data Analysis, 19 (3): 597–616, arXiv:1406.3496, doi:10.3233/IDA-150734, S2CID 17966555
- ↑ Muralidharan, Vivek; Howell, Kathleen (2023), ""Stretching directions in cislunar space: Applications for departures and transfer design"", Astrodynamics, 7 (2): 153–178, Bibcode:2023AsDyn...7..153M, doi:10.1007/s42064-022-0147-z
- ↑ Muralidharan, Vivek; Howell, Kathleen (2022), ""Leveraging stretching directions for stationkeeping in Earth-Moon halo orbits"", Advances in Space Research, 69 (1): 620–646, Bibcode:2022AdSpR..69..620M, doi:10.1016/j.asr.2021.10.028, S2CID 239490016
- ↑ Rijk, P.P.M. de (1989). "A one-sided Jacobi algorithm for computing the singular value decomposition on a vector computer". SIAM J. Sci. Stat. Comput. 10: 359.
- ↑ 22.0 22.1 22.2 Trefethen, Lloyd N.; Bau, David III (1997). Numerical Linear Algebra. Philadelphia: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-361-9.
- ↑ 23.0 23.1 Golub, Gene H.; Kahan, William (1965). "Calculating the singular values and pseudo-inverse of a matrix". Journal of the Society for Industrial and Applied Mathematics, Series B: Numerical Analysis. 2 (2): 205–224. Bibcode:1965SJNA....2..205G. doi:10.1137/0702016. JSTOR 2949777.
- ↑ 24.0 24.1 "Netlib.org".
- ↑ Demmel, James; Kahan, William (1990). "Accurate singular values of bidiagonal matrices". SIAM Journal on Scientific and Statistical Computing. 11 (5): 873–912. CiteSeerX 10.1.1.48.3740. doi:10.1137/0911052.
- ↑ GSL Team (2007). "§14.4 Singular Value Decomposition". GNU Scientific Library Reference Manual.
- ↑ Golub, Gene H.; Van Loan, Charles F. (1996). Matrix Computations (3rd ed.). Johns Hopkins. ISBN 978-0-8018-5414-9.
- ↑ "Simple SVD". MATLAB Central File Exchange.
- ↑ Demmel, James (2000). "Decompositions". Templates for the Solution of Algebraic Eigenvalue Problems. By Bai, Zhaojun; Demmel, James; Dongarra, Jack J.; Ruhe, Axel; van der Vorst, Henk A.. Society for Industrial and Applied Mathematics. doi:10.1137/1.9780898719581. ISBN 978-0-89871-471-5. https://www.netlib.org/utk/people/JackDongarra/etemplates/node43.html.
- ↑ Chicco, D; Masseroli, M (2015). "Software suite for gene and protein annotation prediction and similarity search". IEEE/ACM Transactions on Computational Biology and Bioinformatics. 12 (4): 837–843. doi:10.1109/TCBB.2014.2382127. hdl:11311/959408. PMID 26357324. S2CID 14714823.
- ↑ Fan, Ky (1951), ""Maximum properties and inequalities for the eigenvalues of completely continuous operators"", Proceedings of the National Academy of Sciences of the United States of America, 37 (11): 760–766, Bibcode:1951PNAS...37..760F, doi:10.1073/pnas.37.11.760, PMC 1063464, PMID 16578416
- ↑ Eckart, C.; Young, G. (1936). "The approximation of one matrix by another of lower rank". Psychometrika. 1 (3): 211–8. doi:10.1007/BF02288367. S2CID 10163399.
- ↑ Hestenes, M. R. (1958). "Inversion of Matrices by Biorthogonalization and Related Results". Journal of the Society for Industrial and Applied Mathematics. 6 (1): 51–90. doi:10.1137/0106005. JSTOR 2098862. MR 0092215.
- ↑ Golub, G. H.; Reinsch, C. (1970). "Singular value decomposition and least squares solutions". Numerische Mathematik. 14 (5): 403–420. doi:10.1007/BF02163027. MR 1553974. S2CID 123532178.
本中文词条由刘宇康贡献,张江,王志鹏整理和审校,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。